
高校生になると証明という、
今までとは様子の異なる問題に出逢います。
数学なのに文章で解くことに
難しさと苦手意識を覚える人も多いです。
この記事では、証明問題の答え方を
例文付きでわかりやすく
基本だけに的を絞って説明したいと思います。
証明の仕方
次の簡単な問題を考えます。
例題1
$$a=1 \quad b=2 \hspace{20cm}$$とする時$$a + b = 3 \hspace{20cm}$$であることを証明してください。
証明問題とは
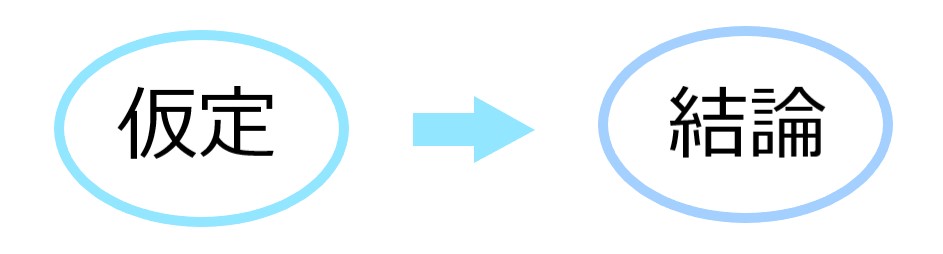
証明問題とは仮定(与えられた条件)から
結論(証明を求められていること)を導く作文問題です。
この問題の場合、
仮定はa=1、b=2で
結論はa+b=3となります。
図にすると
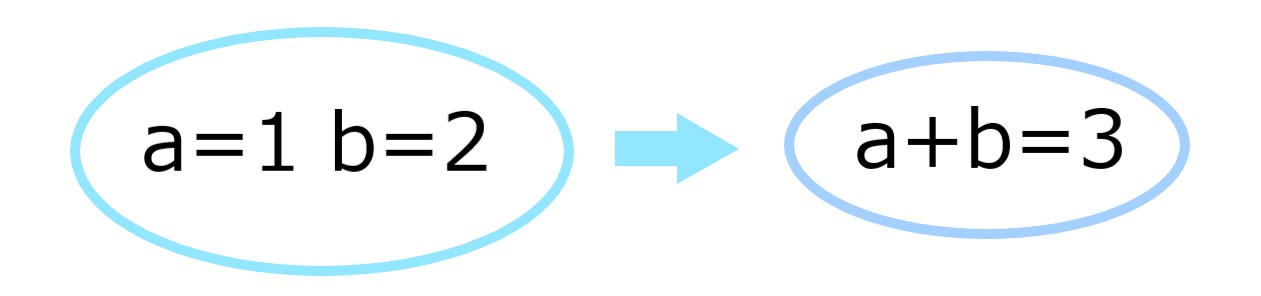
です。
左側の仮定を上手に使って
右側の結論にたどり着けたら正解をもらえます。
実際に解いてみます。
例題1の証明
仮定の$$a=1 \quad b=2 \hspace{20cm}$$を代入することにより$$a + b = 1 + 2 \hspace{20cm}$$である。ここで$$1 + 2 = 3 \hspace{20cm}$$より$$a + b = 3 \hspace{20cm}$$を得る。よって示された。\(\square\)
三段論法と証明
次に、少しだけ問題を難しくします。
例題2
$$a=1 \quad b=2 \hspace{20cm}$$とする時$$a^2 + b^2 = 5 \hspace{20cm}$$であることを証明してください。
仮定は同じくa=1、b=2で
結論はa2+b2=5です。
例題2の証明
仮定の$$a=1 \quad b=2 \hspace{20cm}$$より$$a^2=1 \quad b^2=4 \hspace{20cm}$$である。これらを代入すれば$$a^2 + b^2 = 1 + 4 \hspace{20cm}$$になる。ここで$$1 + 4 = 5 \hspace{20cm}$$なので$$a^2 + b^2 = 5 \hspace{20cm}$$が示される。\(\square\)
証明の手順を図にします。

例題1では仮定から直接、
結論に行けましたが
今回は途中式を挟んで結論にたどり着きました。

A⇒BかつB⇒Cの時A⇒Cなので(三段論法といいます)
この場合も、仮定から結論を導けています。
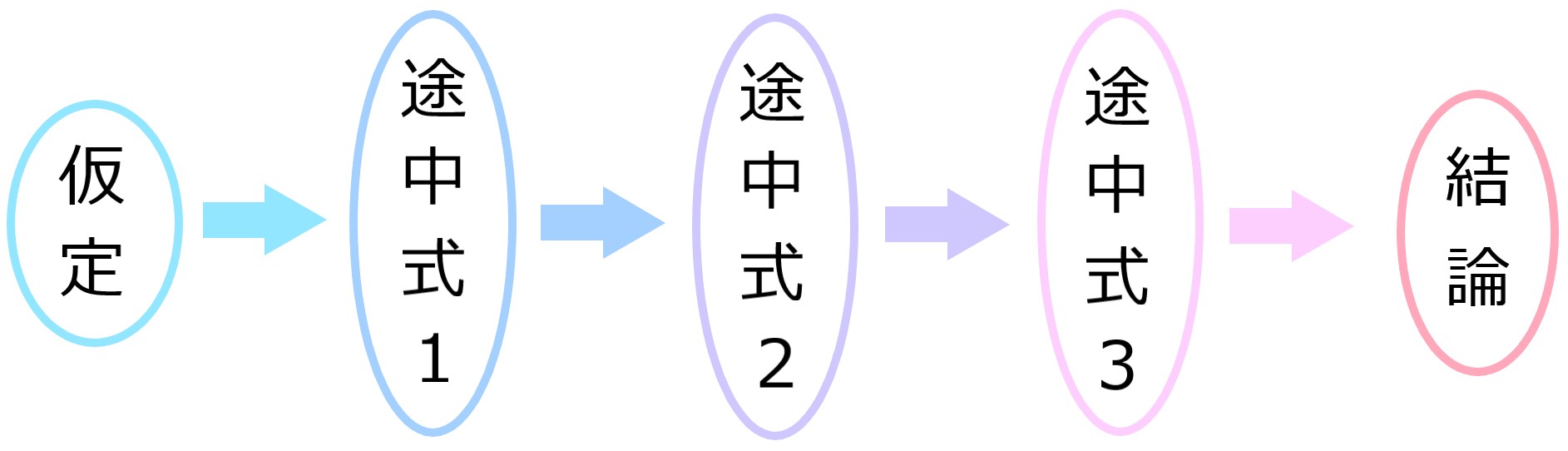
難しい問題ほど間の途中式の数が増えます。
途中式がいくつあっても
仮定から結論まで一本の矢印で結べていれば、
証明問題を解けたことになります。
テンプレートの解き方
最後に証明の書き方の
テンプレートを説明して終わろうと思います。
例題3
$$a=1 \quad b=2 \quad c=3 \hspace{20cm}$$とする時$$ab < c \hspace{20cm}$$であることを証明してください。
例題3の証明
$$ab < c \hspace{20cm}$$であることを示す。
仮定より、$$a=1 \quad b=2 \hspace{20cm}$$なので$$ab=2 \hspace{20cm}$$また$$c=3 \hspace{20cm}$$も仮定である。ここで$$2 < 3 \hspace{20cm}$$なので$$ab < c \hspace{20cm}$$が示される。\(\square\)
始めにすべきこと
証明問題を解くには、
始めに仮定と結論を確認します。
この問題だと
仮定はa=1、b=2、c=3
結論はab<cです。
見分け方としては、
問題文末に書かれている
証明を求められていることが結論で
その他はすべて仮定です。
書き始め
$$ab < c \hspace{20cm}$$であることを示す。
これから証明することを始めに書きます。
問題文から示すべきことが
明らかに読み取れる時は省略可能です。
途中式
仮定より、$$a=1 \quad b=2 \hspace{20cm}$$なので$$ab=2 \hspace{20cm}$$また$$c=3 \hspace{20cm}$$も仮定である。
仮定を上手に使いながら結論に近付きます。
コツは、どの仮定をどんな風に使ったか
読んでいる人に伝わるように書くことです。
また「同様に」、「自明」といった
証明独自の用語がありますが
無理に使わなくても大丈夫です。
先生がチェックしているのは
仮定から結論まで論理展開できているか、なので
自然な自分の言葉で書きましょう。
終わり方
ここで$$2 < 3 \hspace{20cm}$$なので$$ab < c \hspace{20cm}$$が示される。\(\square\)
途中式を根拠に結論を導きます。
締めの文としては、
- (結論)+(示された)
もしくは単に
$$ab < c \hspace{20cm}$$である。\(\mathrm{Q.E.D.}\)
- (結論)+(である)
が一般的です。
文末には四角形を書いて証明の終了を表します。
四角形の代わりにQ.E.D.
と書く流儀もありますが
大体の人は四角形です。

