
弧ABに対する角∠APBは
点Pが円周上にある限り常に等しい、
というのが円周角の定理でした。
応用で点Pが円の外、内側にある場合
∠APBは円周角より
小さく、大きくなります。
この性質を三角形の角度についての定理を利用して
わかりやすく証明したいと思います。
基本となる定理
三角形の角度について次が成り立ちます。
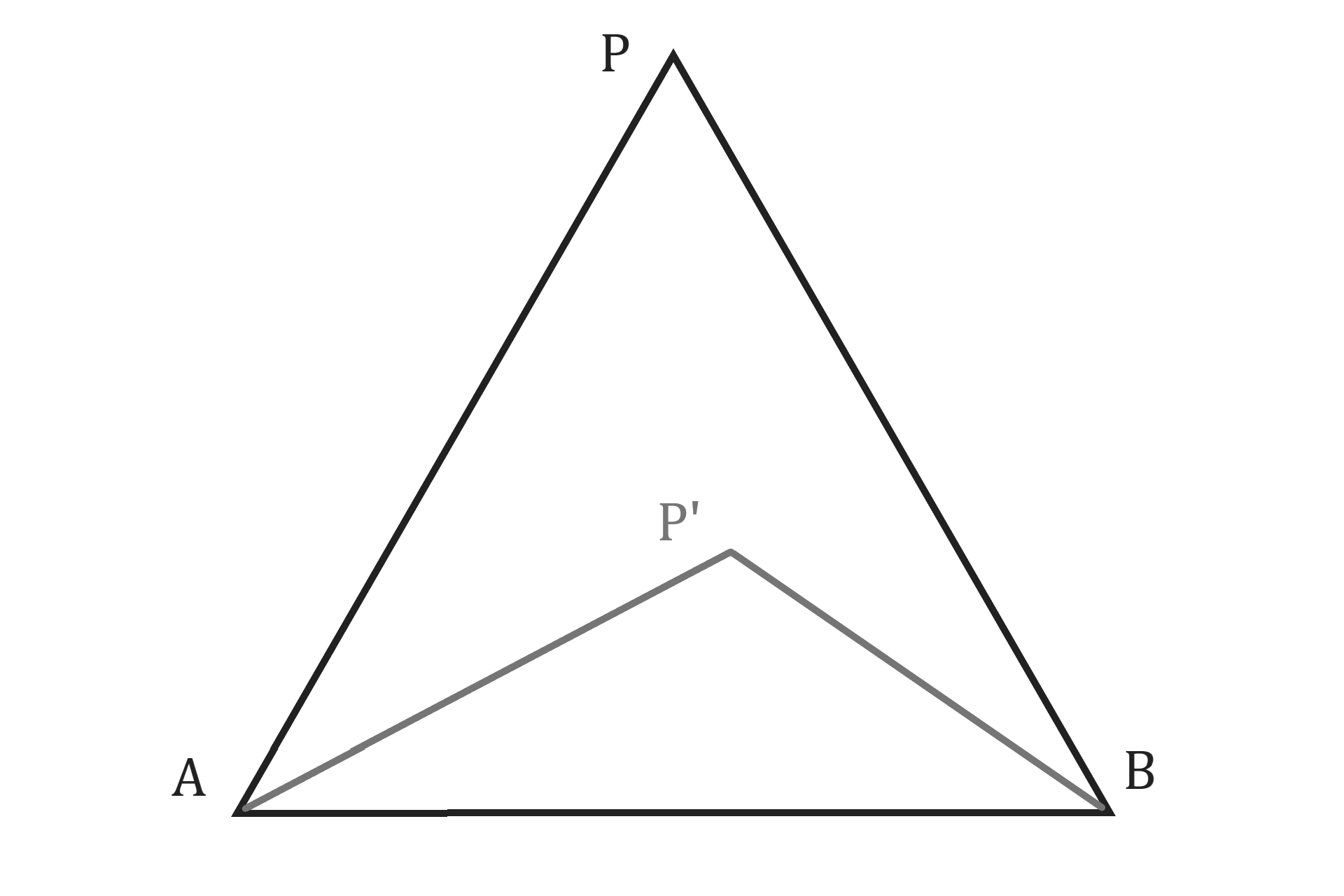
三角形ABPの内部に点P'がある時
\( \angle \mathrm{APB} < \angle \mathrm{AP'B} \)
証明
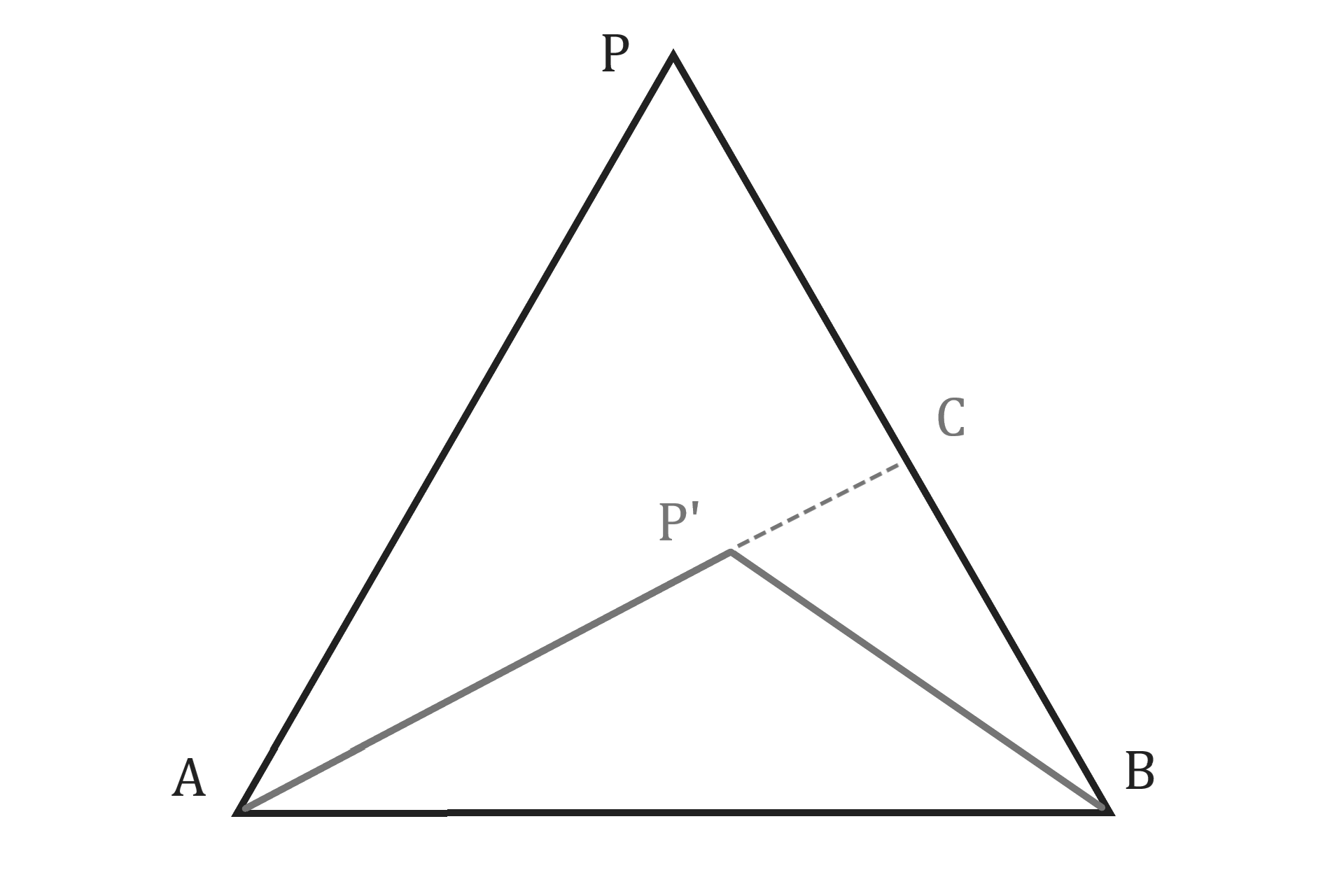
AP'の延長と辺PBとの交点をCと置いて
補助線P'Cを引く。
∠P'CBは三角形ACPの外角なので
\( \angle \mathrm{P'CB} = \angle \mathrm{APB} +\angle \mathrm{PAC} \quad \cdots (1) \)
また∠AP'Bは三角形P'BCの外角なので
\( \angle \mathrm{AP'B} = \angle \mathrm{P'CB} +\angle \mathrm{CBP'} \)
式(1)を右辺に代入して
\( \angle \mathrm{AP'B} = \angle \mathrm{APB} +\angle \mathrm{PAC} +\angle \mathrm{CBP'} \)
を得る。
∠AP'Bは∠APBより∠PACと∠CBP'だけ大きいので
\( \angle \mathrm{APB} < \angle \mathrm{AP'B} \quad \square \)
定理の仮定
3点A、B、Qは円周上の点、
すなわち∠AQBは円周角とします。
円の外部と内部に点Pをとり
∠APBと∠AQBを比べます。
円周角の定理の系
円の外
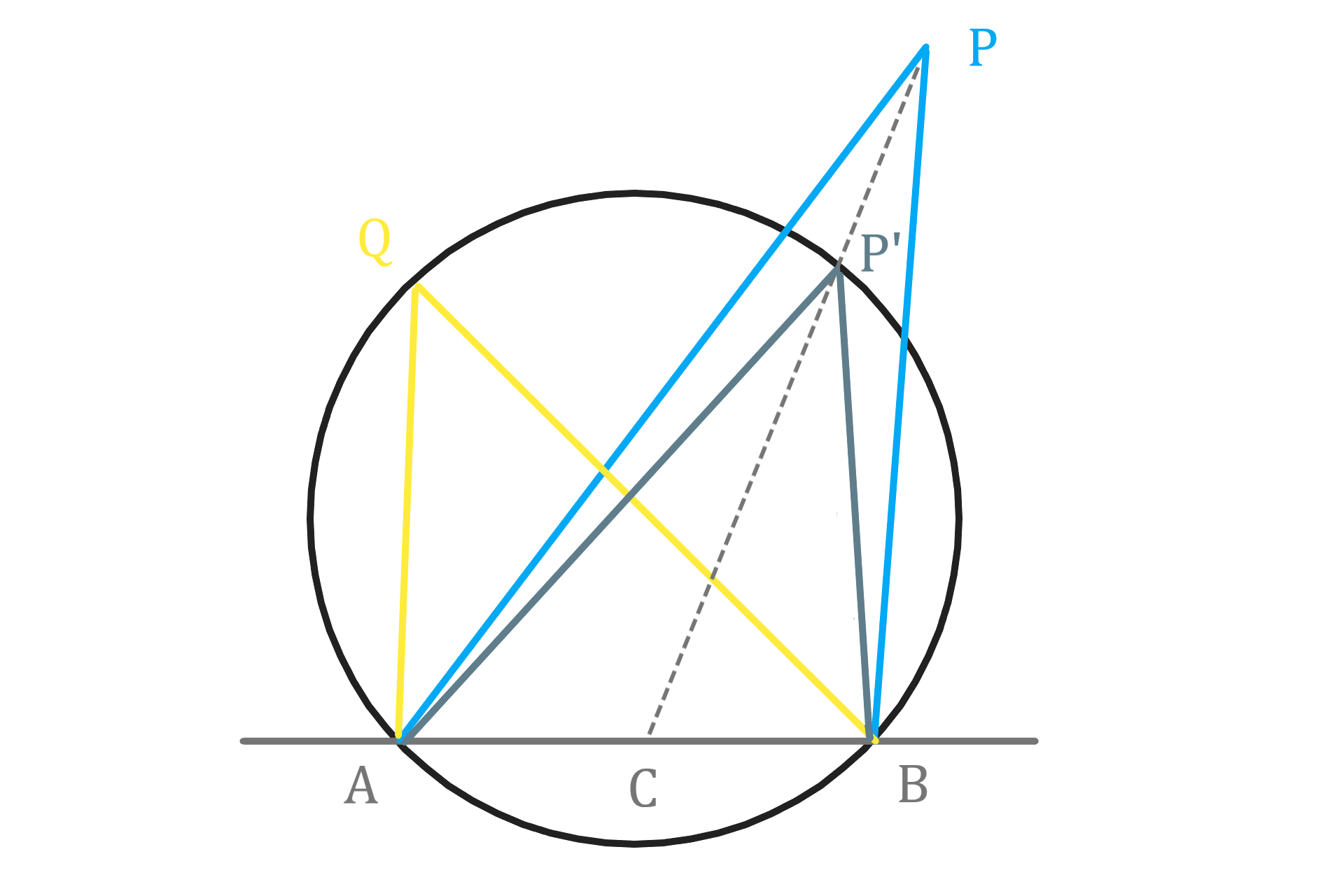
線分AB上にA、Bとは異なる点Cをとり
CPと円との交点をP'とする。
先の定理より
\( \angle \mathrm{APB} < \angle \mathrm{AP'B} \)
また円周角の定理より
\( \angle \mathrm{AQB} = \angle \mathrm{AP'B} \)
なので
\( \angle \mathrm{APB} < \angle \mathrm{AQB} \quad \square \)
円の内
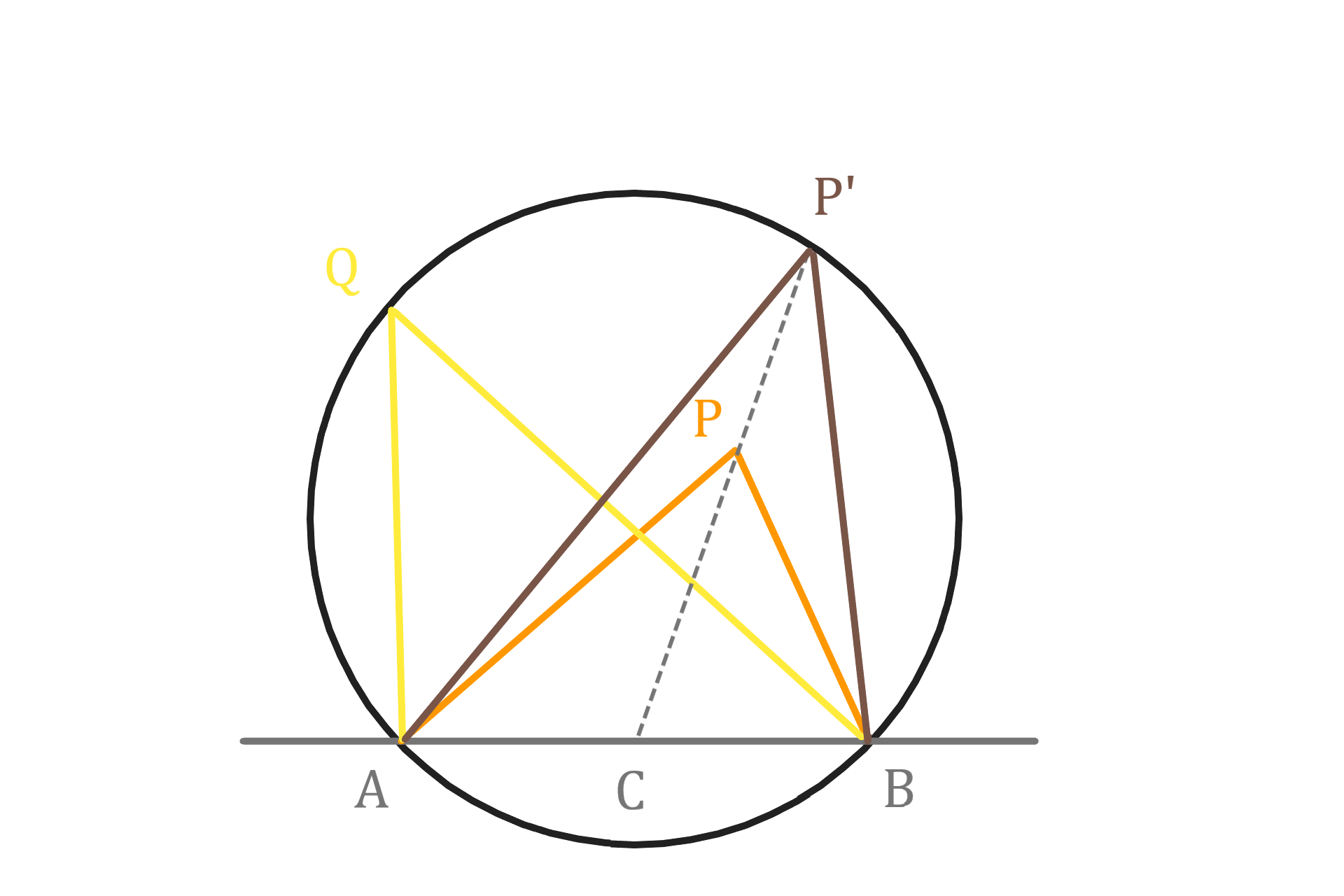
線分AB上にA、Bとは異なる点Cをとり
CPの延長と円との交点をP'とする。
先の定理より
\( \angle \mathrm{AP'B} < \angle \mathrm{APB} \)
また円周角の定理より
\( \angle \mathrm{AQB} = \angle \mathrm{AP'B} \)
なので
\( \angle \mathrm{AQB} < \angle \mathrm{APB} \quad \square \)
まとめ
直感的に明らかな
三角形の角度の大小関係があり、
円周角の定理で
その形に持ち込みます。
今回示した事実は
円周角の定理の逆の証明に使われます。
