
中学生になると平方根(√:ルート)という
今までとは雰囲気の異なる数字を勉強します。
小数や分数などに比べて
とっつきづらい、このルート…
好きになってもらえるよう√2に焦点を当てて
私たちの生活に見られる活用例を紹介して行きます。
芸術(デザイン)に
√2は長さ1の正方形の対角線に現れます。
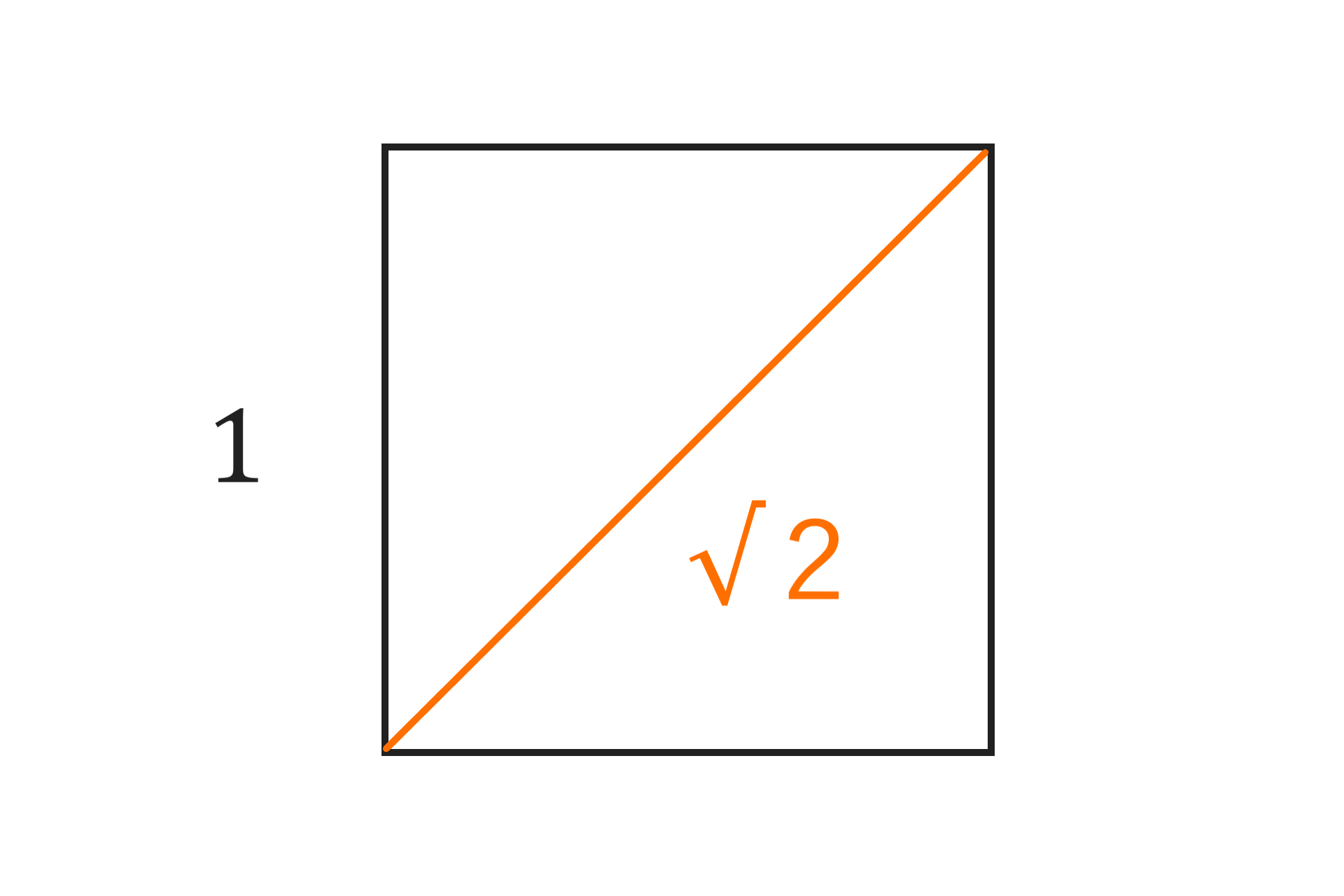
この辺と対角線のバランス
$$ 1 : \sqrt{2} $$
に人は美しさを感じるため
デザインに見る事ができます。
歴史上の建築物では例えば、
法隆寺の金道や五重塔がこの大和比になっています。

昔の人も美しさを求めた結果、
自然とこの比率にたどり着いたのでしょう。
現在で言うと東京スカイツリー、
ドラえもん、アンパンマン、キティちゃんの顔も大和比です。
デザイナーの人から意識されている比率です。
ちなみに
$$ 1 : \sqrt{3} $$
も白金比と呼ばれ美しいとされます。
日用的な使われ方
A版サイズ、B版サイズ
美しさに加えて実用性もあります。
A4、A3と言った紙のサイズ(B4、B3も)
は縦横が大和比になるよう作られています。
理由は2等分した時
同じ形(相似)なまま小さな長方形になるから、です。
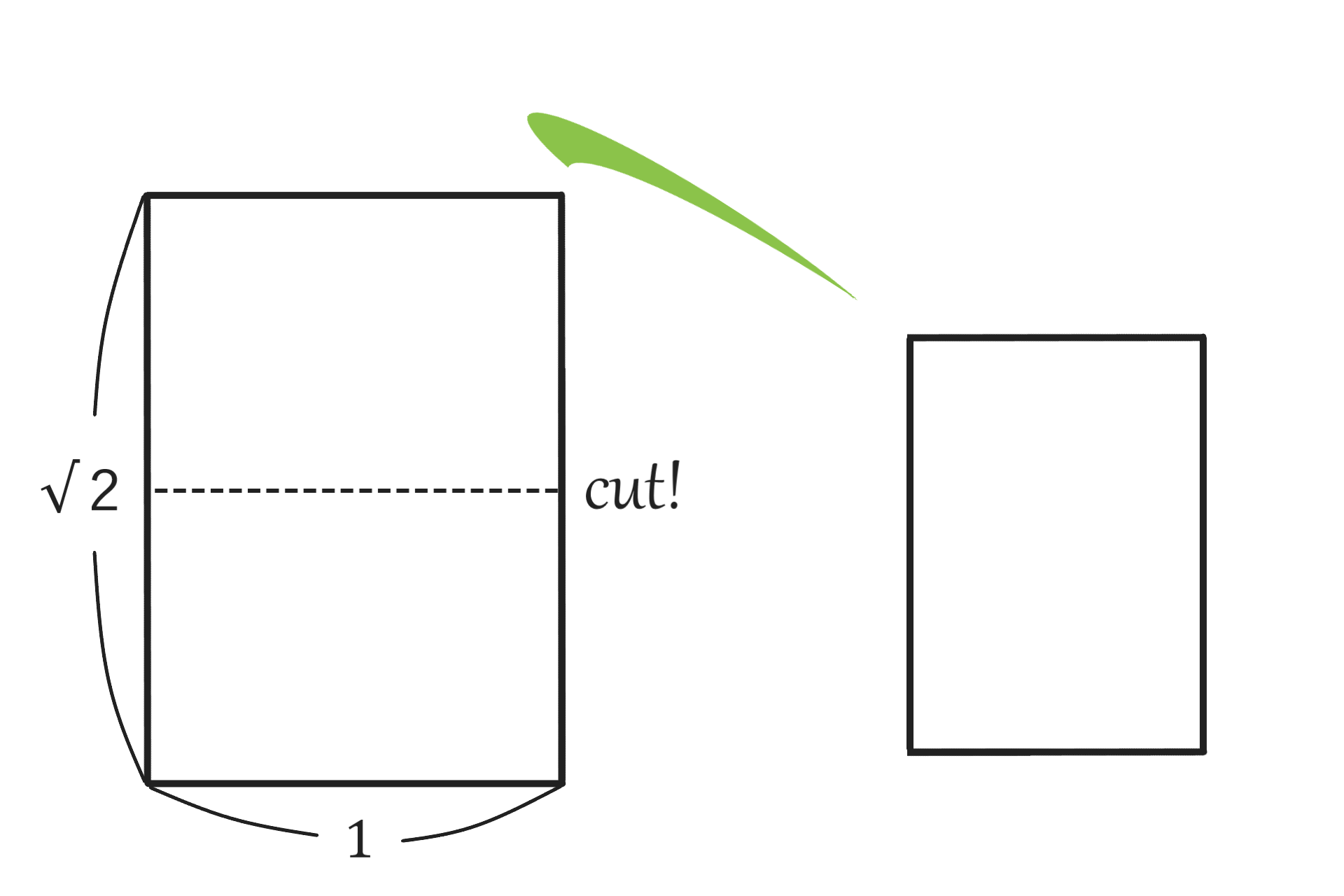
証明
2等分してできる長方形の縦横は
$$ 1 : \frac{\sqrt{2} }{2} \hspace{20cm} $$
である。
分母と分子を√2で割って
$$ = 1 : \frac{1}{\sqrt{2} } \hspace{20cm}$$
√2を掛けて
$$ = \sqrt{2} : 1 \hspace{20cm} $$
なので始めと同じ縦横比。\( \square \)
A1サイズの紙を半分に切るとA2が二枚できる、
という仕組みになっていて
大きいサイズの紙から必要に応じて
小さいサイズの紙を作れる便利さを持ちます。
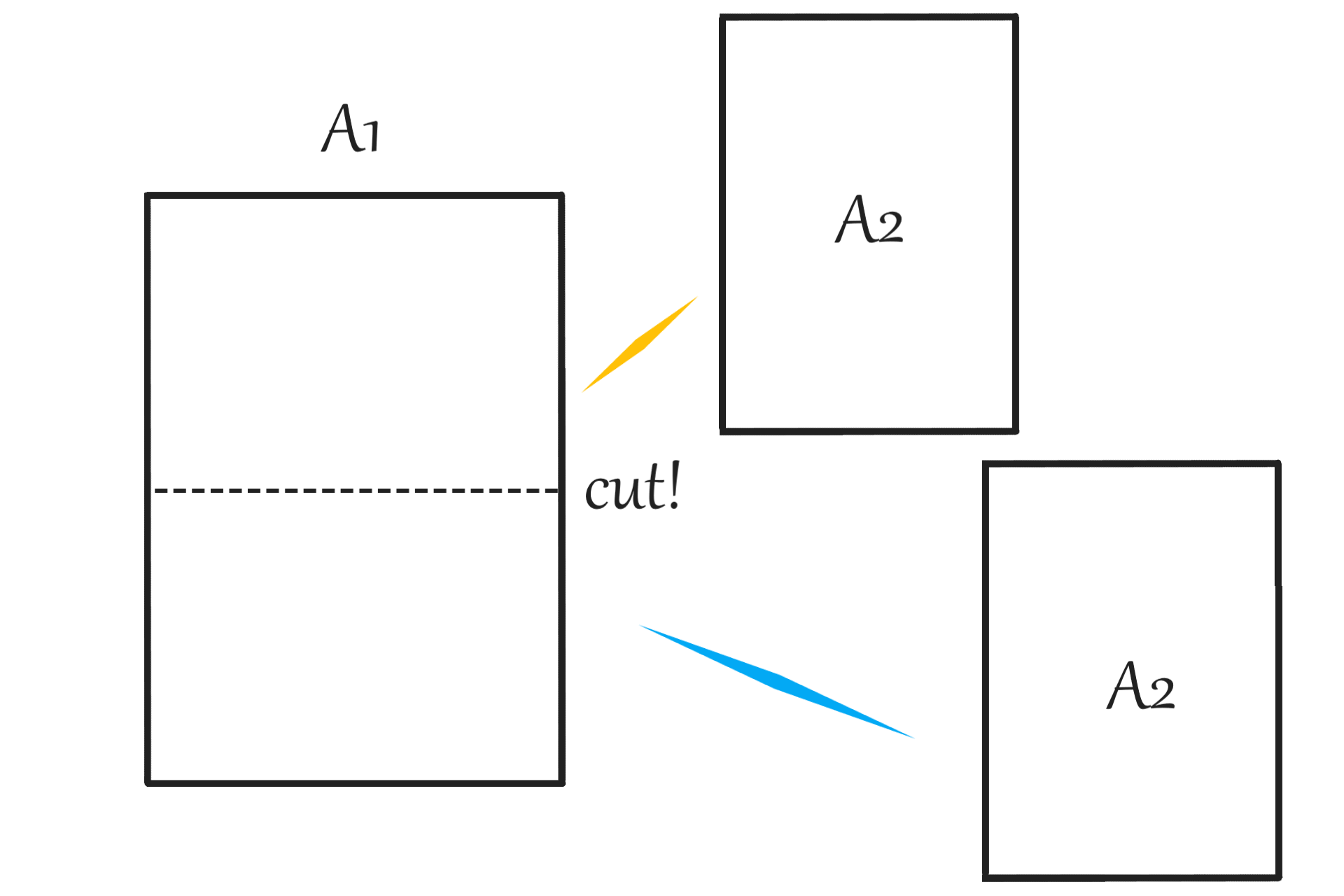
おまけに2つ上のサイズで
ちょうど倍の大きさになります。
直感的にも分かりやすいです。
カメラの絞り
図形を√2倍に拡大すると面積は2倍になります。
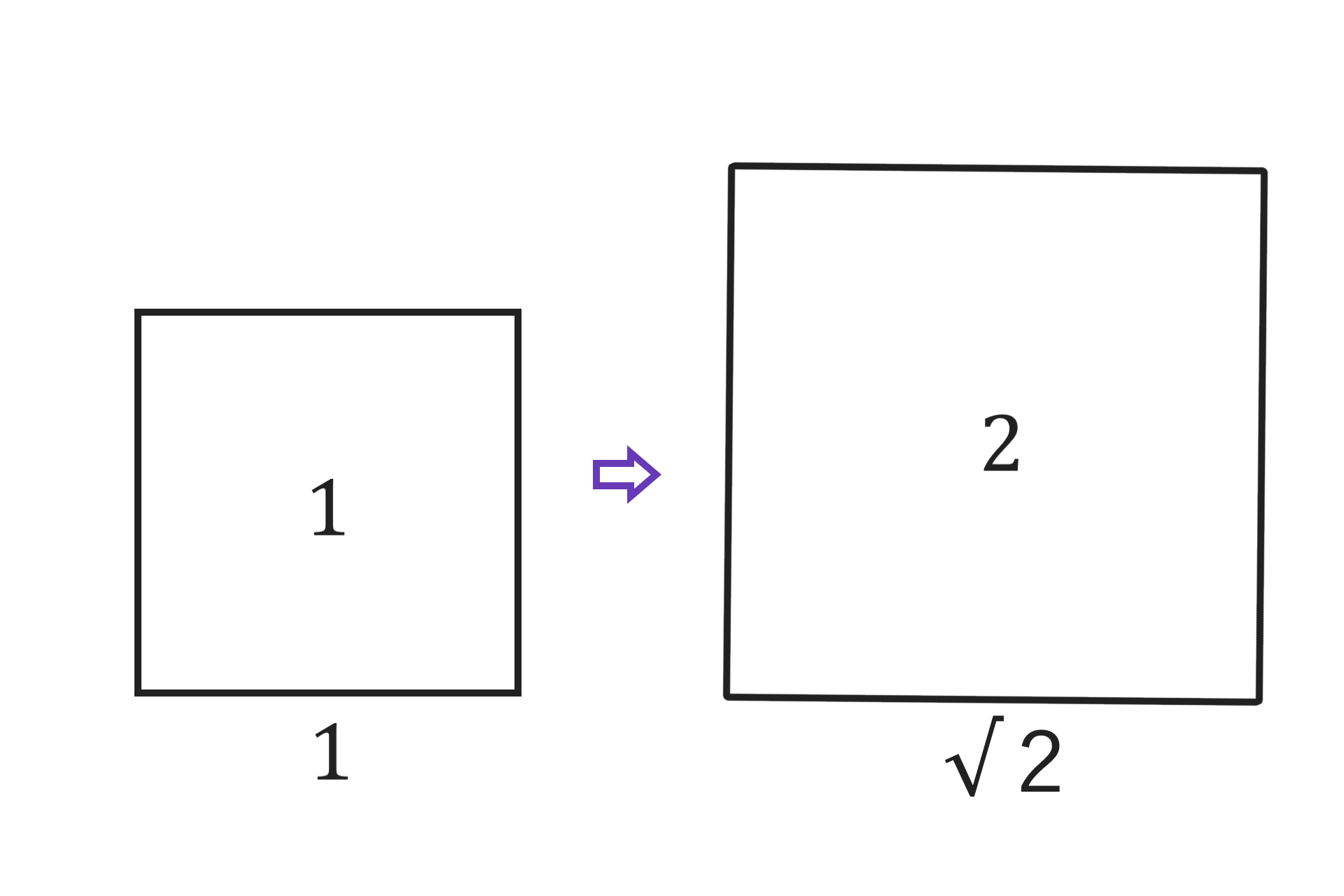
この性質はカメラの絞りに応用されています。
2倍の量の光をカメラに取り込んで
写真を撮りたい時は、絞りを√2倍に開きます。
√2倍ずつの目盛りが付いてます。

\( \sqrt{2} \fallingdotseq 1.4 , \quad \sqrt{2}^2 = 2 , \quad \sqrt{2}^3 \fallingdotseq 2.8, \cdots \)
調節して明るさを倍々に増やせます。
建築技術、物理学にも
平方根をなぜ学校で習うかと言うと
三平方の定理
\( a^2 + b^2 = c^2 \)
のためです。
ルートのおかげで
\( c = \sqrt{a^2 + b^2 } \)
として三角形の斜辺が求まります。
そして斜辺が求まると三角比
$$ \sin 45^{\circ} = \frac{1}{\sqrt{2} } \hspace{20cm} $$
が分かります。
さらに三角比を使うと正確な測量ができて
みんなの住む家を作る建築技術が向上、
また三角関数も作れて
こちらは波を表す関数として
物理学で重要な役割を果たします。
まとめ
身の回りの√2が使われている物は
- デザイン
- 紙のサイズ
- カメラの絞り
- 建築技術
- 物理学
です。
デザイナー、建築士、物理学者さんは特に
ルートと関係の深い職業と言えます。
私たちも普段手にしている紙に
√2が隠れていたり、
写真撮影に便利な図形的な性質があったり
地味にお世話になってます。
