
一番くじを引くのに便利な
確率と、くじ結果のシミュレートツールです。
くじ箱の中の、残りのくじ枚数を入力するだけで
何枚引いた時、欲しい景品が
何%の確率で当たるか分かるよう作りました。
詳しい使い方はツールの後に説明します。
一番くじシミュレーター
くじ結果シミュレーション
| 残り個数 | |
|---|---|
| A賞 | |
| B賞 | |
| C賞 | |
| D賞 | |
| E賞 | |
| F賞 | |
| G賞 | |
| H賞 | |
| I賞 | |
| J賞 | |
| K賞 | |
| L賞 |
シミュレーション結果
| 賞 | 当選個数 |
|---|
使い方
一番くじオンラインなら、お好きなくじ箱を選んで
店頭の一番くじなら、掲示されている
残りのくじ枚数を入力します。
具体的に、
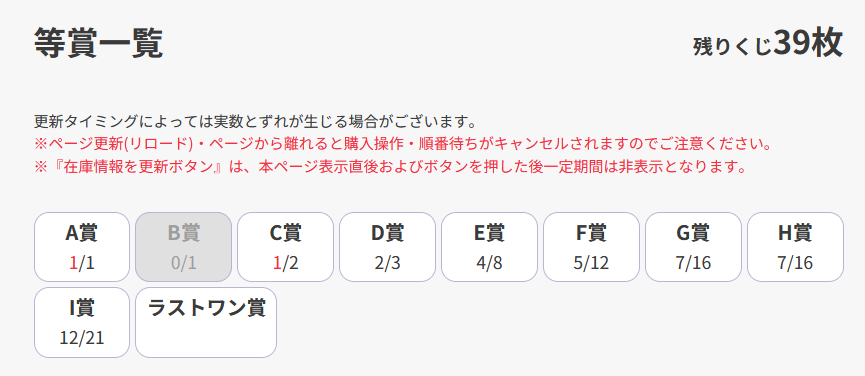
この場合は残りのくじ枚数の欄に39を入力します。
確率を計算
ボタンを押すと表が作成されます。

表は+ボタンを押すと見れます。
次に、自分にとっての当りは何個か数えます。
例えばA、B、C賞狙いの人にとって、
このくじ箱の中の当りは2個になります。
(A賞1個)+(B賞0個)+(C賞1個)=2個
D賞も欲しい人の当りは4個、
E賞でも良い人にとって当りは8個です。
欲しい景品の当たる確率(少なくとも一つ当たる確率)
の表を見て
何枚引くと、何%の確率で当たるか調べられます。
- 少なくとも二つ当たる確率
- 少なくとも三つ当たる確率
の表は、当りの中から
二つ以上、三つ以上を当てたい時に見ます。
両方とも当たる確率
二種類の景品を両方もらえる確率です。
例えば、A賞とC賞を当てたい人は
- 景品Aの残り数に1
- 景品Bの残り数に1
A賞1/1、C賞1/2
を入力。
確率を計算
ボタンを押して、
どのくらい難しいか確認できます。
応用
賞という枠組みに囚われず
他にも、くじ箱の中の
- フィギュアが3個
- ぬいぐるみが4個
の時は、3と4を入力して、
フィギュアとぬいぐるみ両方を当てる確率なども見れます。
景品をグッズの種類で分けたり
キャラで分けたり
景品A、景品Bの数え方を工夫すると色々できます。
三つすべて当たる確率
同じく、項目を一つ増やして、
三つとも当たる確率を計算します。
例えば
- タペストリー
- マグカップ
- アクリルスタンド
すべて当たる確率を調べられます。
くじ結果シミュレーション

- くじ箱の中の各賞の残り個数
- くじを引く回数
を入力して、くじ結果を体験できます。
入力欄は多めにL賞まで用意してます。
無かった場合は0のままで大丈夫です。
シミュレーション実行
ボタンを押すごとに抽選結果が表示されます。
まとめ
説明は以上となります。
一番くじは人気が高く利用する人も多いので、
気合を入れて作ってみました。୧(⑉•̀ㅁ•́⑉)૭✧
使い方が少し複雑になってしまいましたが…
役に立ったら良いな、と思います。
数学に興味ある人向けの説明
シミュレーションに用いた数式を軽く説明します。
景品Aの当たる確率(少なくとも1つ当たる確率)
を計算するには
景品Aの当たらない確率を1から引き算します。
すなわち
引く回数をn、景品Aの残り個数をa、残りのくじ枚数をmとすると
$$ 1 -\prod_{i=0}^{n-1} \frac{(m-a)-i}{m-i} \hspace{20cm}$$
がくじをn回抽選した時の景品Aの当たる確率です。
さらに、n回抽選した際
景品Aの当たった回数が丁度k回である確率は、
二項係数を利用して
$$ {}_n \mathrm{C}_k \left( \prod_{i=0}^{k-1} \frac{a-i}{m-i} \right) \left( \prod_{j=0}^{n-k-1} \frac{m-a-j}{m-k-j} \right) \hspace{20cm}$$
と書けます。
例えばk=1の場合は
景品Aが丁度1つ当たる確率になり、
これを、先程の
景品Aが少なくとも1つ当たる確率から引き算すると
景品Aが少なくとも2つ当たる確率、を求められます。
続けて、景品Aが丁度2つ当たる確率を引くと
景品Aが少なくとも3つ当たる確率、を求められます。
両方とも当たる確率
景品AとBの両方を当てる確率P(A∩B)は
景品Aの当たる確率P(A)、景品Bの当たる確率P(B)、
景品AまたはBの当たる確率P(A∪B)を用いて
$$ \mathrm{P}(\mathrm{A} \cap \mathrm{B} ) = \mathrm{P}(\mathrm{A}) +\mathrm{P}(\mathrm{B}) -\mathrm{P}(\mathrm{A} \cup \mathrm{B} ) \hspace{20cm}$$
です。
ここで景品AまたはBの当たる確率は
景品Bの残り個数をbとして
$$ 1 -\prod_{i=0}^{n-1} \frac{(m-a-b)-i}{m-i} \hspace{20cm}$$
により与えられます。
景品A、B、Cの3つとも当たる確率P(A∩B∩C)も同様に
有名な公式
$$ \mathrm{P}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C} ) = \mathrm{P}(\mathrm{A}) +\mathrm{P}(\mathrm{B}) +\mathrm{P}(\mathrm{C}) \hspace{20cm}$$
$$ -\mathrm{P}(\mathrm{A} \cup \mathrm{B} ) -\mathrm{P}(\mathrm{B} \cup \mathrm{C} ) -\mathrm{P}(\mathrm{C} \cup \mathrm{A} ) +\mathrm{P}(\mathrm{A} \cup \mathrm{B} \cup \mathrm{C} ) $$
を利用して計算します。
ここで景品AまたはBまたはCの当たる確率P(A∪B∪C)は
景品Cの残り個数をcとして
$$ 1 -\prod_{i=0}^{n-1} \frac{(m-a-b-c)-i}{m-i} \hspace{20cm}$$
により与えられます。
これらの数式をプログラミングして、
計算結果を表にまとめてます。
くじの抽選結果のシミュレーションは、
ランダム関数を抽選回数だけ走らせています。
