
シャドバ、ハースストーン、MTG、
カードゲームで遊ぶとき手札はランダムに配られます。
「自分の欲しいカードはどのくらいの確率で来るのか…」
を知っていた方が、有利にゲームを進められることは明らかです。
この記事ではカードゲームで良く使う確率の求め方を解説します。
欲しいカードを引ける確率
全部で40枚のデッキの中にカードAが10枚入ってます。
5枚ドローする間に、
カードAを引いて来れる確率はいくらでしょう。
この確率を計算するに当たって、
”求めたい確率の逆を計算する”というテクニックを使います。
下のベン図の様に、
事象「カードAを引ける」と事象「カードAを引けない」は
お互いに補集合の関係にあります。
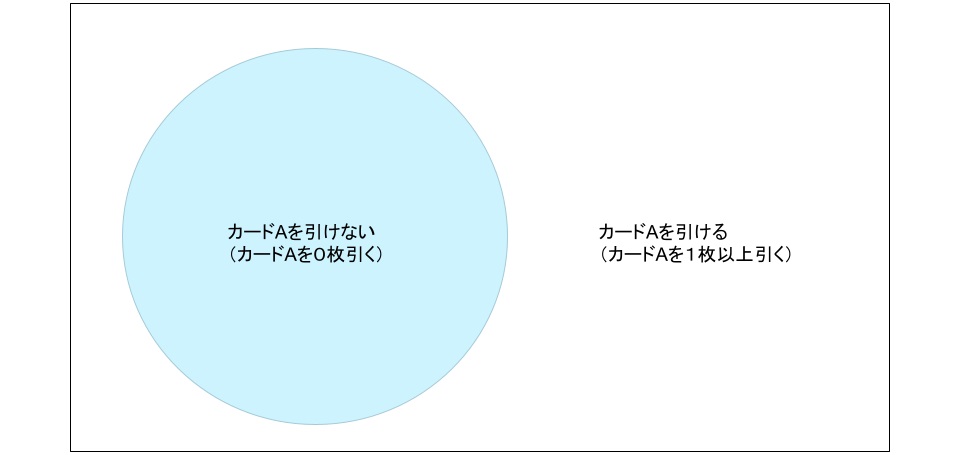
カードAを引けない確率を求めて、1から引き算すると
カードAを引ける確率になる理由です。
では5枚ドローしてもカードAを引けない確率を求めて行きます。
デッキ40枚中、カードAでないカードは30枚入ってるので
1枚目のドローでカードAを引けない確率は30/40です。
続けて2枚目のドローの時には、
デッキの枚数は39枚
カードAでないカードの枚数は29枚に減ってるので
2枚連続でカードAを引けない確率は30/40×29/39です。
これを5回繰り返すので、
$$\frac{30}{40}\times\frac{29}{39}\times\frac{28}{38}\times\frac{27}{37}\times\frac{26}{36}=\frac{609}{2812} \hspace{20cm}$$
が求める確率になります。
609/2812を1から引き算すると2203/2812 ≒ 0.78342なので
この問題では約78%の確率でカードAを引けることになります。
計算はソフトに任せる
確率の問題はよく階乗の計算になるので
答えはエクセル等のソフトを使って求めます。
手計算で解こうとすると大変です…。
複数枚引ける確率
少しだけ問題文を書き換えて、
全部で40枚のデッキの中にカードAが10枚入ってます。
5枚ドローする間に、
カードAを2枚以上引いて来れる確率はいくらでしょう。
今度はカードAを2枚以上、手札に抱えておける確率です。
(強いカードはたくさんある方が良いので)
先ほどのベン図に、
事象「カードAを1枚だけ引く」を書き加えます。
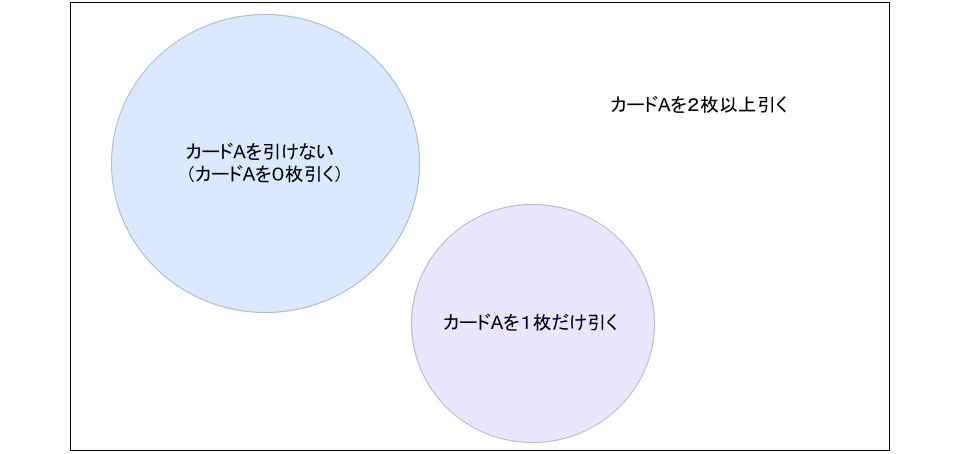
図を見ると
先の答えからカードAを1枚だけ引く確率を引き算すると、
カードAを2枚以上引く確率になることが分かります。
カードAを1枚だけ引く場合には例えば、
1枚目でカードAを引き、
残りの4枚は全部カードA以外、の時があります。
これの確率は
$$\frac{10}{40}\times\frac{30}{39}\times\frac{29}{38}\times\frac{28}{37}\times\frac{27}{36} \hspace{20cm}$$
です。
他にも2枚目でカードAを引き、
残りでカードA以外の時もあります。
こっちの確率は
$$\frac{30}{40}\times\frac{10}{39}\times\frac{29}{38}\times\frac{28}{37}\times\frac{27}{36} \hspace{20cm}$$
かけ算は順番を入れ替えても同じ計算結果になるので、
上の二つの確率は等しいことに注意します。
結局、カードAを1枚だけ引く場合とは
1~5枚目のいずれかでカードAを引いて、
残りの全てでカードA以外を引く事であるので
$${}_5\mathrm{C}_1\times\frac{10}{40}\times\frac{30}{39}\times\frac{29}{38}\times\frac{28}{37}\times\frac{27}{36} \hspace{20cm}$$
でカードAを1枚だけ引く確率は求まります。
これをカードAを引ける確率(カードAを1枚以上引く確率)
から引き算して、カードAを2枚以上引く確率を手に入れます。
続けて、カードAを2枚だけ引く確率は
$${}_5\mathrm{C}_2\times\frac{10}{40}\times\frac{9}{39}\times\frac{30}{38}\times\frac{29}{37}\times\frac{28}{36} \hspace{20cm}$$
で求まり同じ様に引き算すると、
今度はカードAを3枚以上引く確率が手に入ります。
この工程をソフトに繰り返させれば
何枚以上引く確率でも求まります。
コンボの成立する確率
カードゲームにおいてコンボは勝利に直結する大事な要素です、
コンボが成立する確率を計算してみます。
全部で40枚のデッキの中に
カードAが12枚、カードBが18枚入ってます。
5枚ドローする間に、
カードAとB両方を引いて来れる確率はいくらでしょう。
ベン図は次の通り、
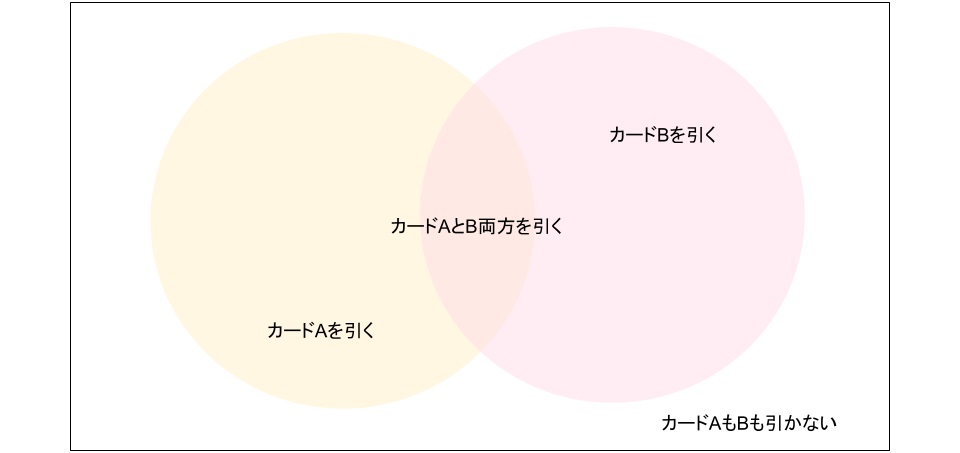
真ん中の重なってる部分の確率を求めます。
図を見ると、
(カードAを引く確率)+(カードBを引く確率)
+(カードAもBも引かない確率)-1
で(カードAとB両方を引く確率)になることに気付きます。
カードAを引く確率、カードBを引く確率の求め方は前述の通り。
カードAもBも引かない確率については、
まず(カードAの枚数)+(カードBの枚数)=12+18=30なので
デッキの中に
カードAでもBでもないカードは40-30=10枚入ってます。
なので5回連続でカードAもBも引かない確率は
$$\frac{10}{40}\times\frac{9}{39}\times\frac{8}{38}\times\frac{7}{37}\times\frac{6}{36} \hspace{20cm}$$
です。
初手の引き直し(マリガン)
欲しいカードを狙って、
初手の引き直し(マリガン)をする際の確率も考えてみます。
全部で40枚のデッキの中にカードAが10枚入ってます。
始めに3枚配られて、3枚までなら引き直せるとします。
ゲーム開始後、5枚ドローするまでに
カードAを引ける確率はいくらでしょう。
この問題で難しいのは、
初手にカードAがあるかどうかで
プレイヤーの取る行動が変わってしまうことです。
始めに配られた3枚にカードAがあれば、そのままキープ
無ければ3枚すべて引き直して探しに行きます。
ベン図は初手にカードAの
ある時、ない時に場合分けして次の様にします。
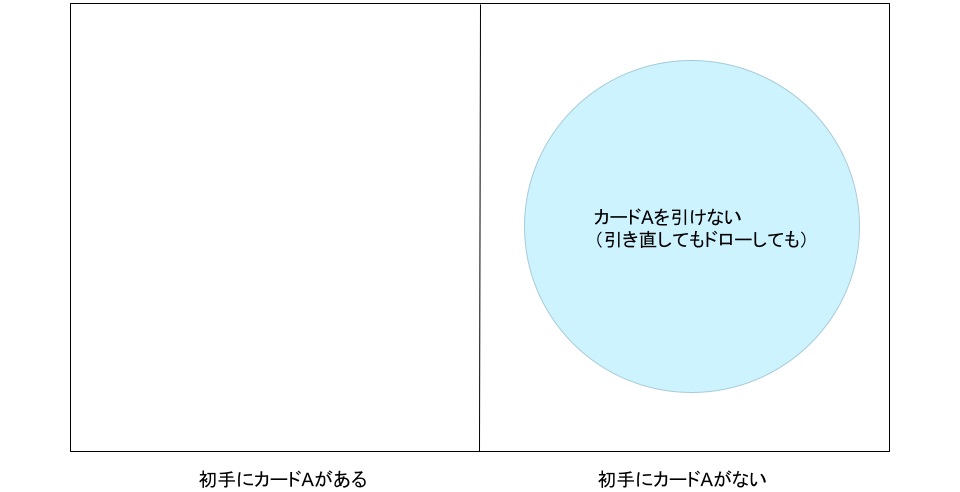
カードAにたどり着けないのは
初手にカードAがなく、
引き直してもドローしても引けない時だけなので
結局この問題も青い部分の確率を
1から引き算する方法で解けます。
始めの3枚の手札にカードAがない確率は、
$$\frac{30}{40}\times\frac{29}{39}\times\frac{28}{38} \hspace{20cm}$$
3枚引き直して、それでも来ない確率は
$$\frac{30}{40}\times\frac{29}{39}\times\frac{28}{38}\times\frac{27}{37}\times\frac{26}{36}\times\frac{25}{35} \hspace{20cm}$$
始めに配られた3枚をデッキに戻してシャッフルし
ゲーム開始後5枚ドローしたのに、
まだカードAが来てくれない確率は
$$\left(\frac{30}{40}\times\frac{29}{39}\times\frac{28}{38}\times\frac{27}{37}\times\frac{26}{36}\times\frac{25}{35}\right) \hspace{20cm}$$
$$\quad \times\left(\frac{27}{37} \times\frac{26}{36}\times\frac{25}{35}\times\frac{24}{34}\times\frac{23}{33}\right) \hspace{20cm}$$
です。
これは約0.02865で、1から引き算すると0.97135
カードAを求めて初手を引き直すと
97%たどり着けることがわかりました。
複数枚、コンボの成立する確率についても基本は同じです。
ですが場合分けの量が増えるので大変です…。
ガチャに応用
ここまでの話は、ガチャの確率にも使えます。
あるソシャゲのガチャでは
☆3キャラが3%の確率で当たります。
10連ガチャで、
☆3キャラを手に入れられる確率はいくらでしょう。
☆3以外の当たる確率は97%なので求める確率は、
$$1-\left(\frac{97}{100}\right)^{10}=0.2625 ... \hspace{20cm}$$
約1/4です。
ガチャの場合は次に当たる確率が一定なので、
すっきりした計算式になります。
まとめ
以上、カードゲームでよく使われる確率の計算方法でした。
これらを計算ソフトの力を借りつつ応用すれば、
大体のカードゲーム関連の確率の問題は解けます。
シャドバ用のエクセルシート
実際に確率論を使ってエクセルシートを作りました。
遊びながら勉強できるゲーム
ゲームと勉強を両立したい人におすすめの記事です♪


