
この記事では長方形の面積、直方体の体積を利用した簡単な方法で、
乗法の交換法則・結合法則を証明したいと思います。
正の数について示した後、負の数に拡張する手順で説明します。
乗法の交換法則の証明
始めに乗法の交換法則を確認します。
・乗法の交換法則
aとbを正の数とした時$$ab=ba$$が成り立つ。
これは、
$$2\times3=3\times2$$
だったり
$$4\times7=7\times4$$
の様に、「かけ算は位置を交換しても答えが同じ」という法則です。
この証明には長方形の面積を利用した方法が簡単です。
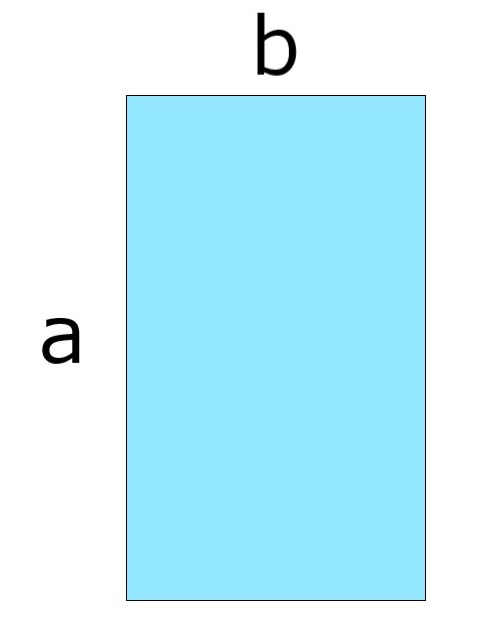
たての長さa、よこの長さbの長方形を考えます。
(長方形の面積)=(たて)×(よこ)
なので、この長方形の面積はabです。
次に、この長方形を横に倒してみます。
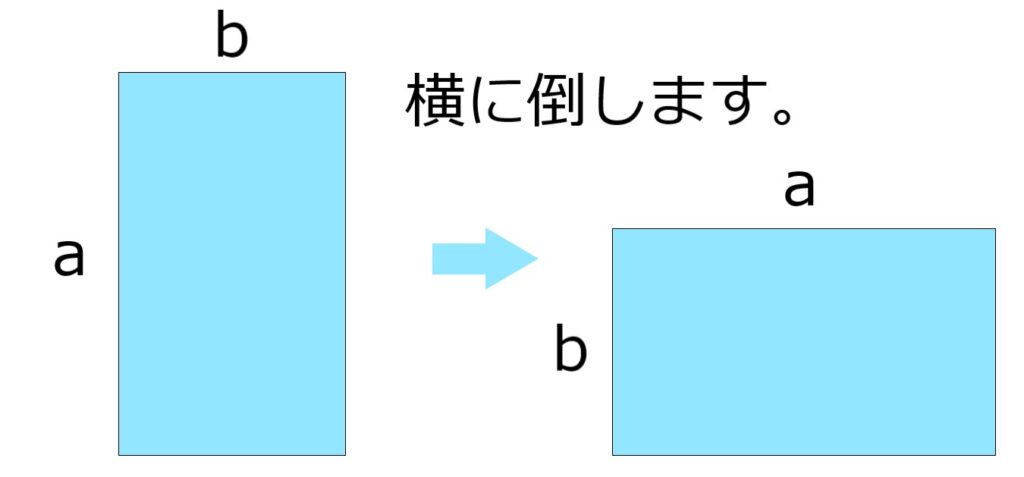
すると今度は、
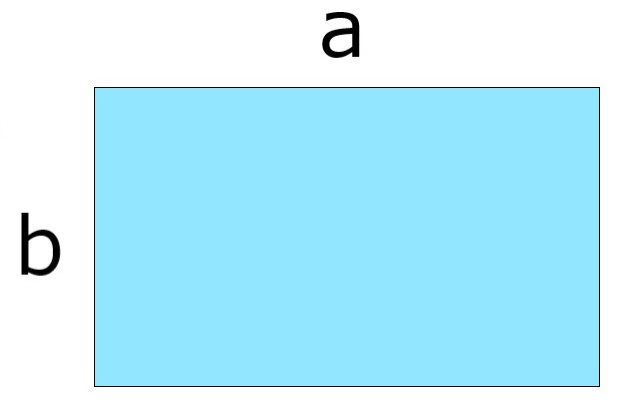
たての長さb、よこの長さaの長方形になるので
面積はbaです。
ここで一つ目の長方形と二つ目は、
横に倒しただけの同じものなので面積も同じです。
以上より、
$$ab=ba$$
を証明できました。
乗法の交換法則の証明(負の数)
乗法の交換法則は負の数にも成り立ちます。
例えば、
aとbを正の数として$$(-a)\times b=b\times(-a)$$
を示します。
左辺は、
$$(-a)\times b=-ab$$
一方、右辺は
$$b\times(-a)=-ba$$
です。
先ほどab=baは証明済みなので
$$(-a)\times b=b\times(-a)$$
になります。
乗法の結合法則の証明
続けて乗法の結合法則も証明したいと思います。
・乗法の結合法則
a、b、cを正の数とした時$$(a\times b)\times c=a\times(b\times c)$$が成り立つ。
これは例えば、
$$2\times 3\times 4$$
を
$$(2\times 3)\times 4=6\times 4=24$$
と計算しても、
$$2\times (3\times 4)=2\times 12=24$$
でも答えは同じ24になる法則のことです。
証明には直方体の体積を利用すると簡単です。
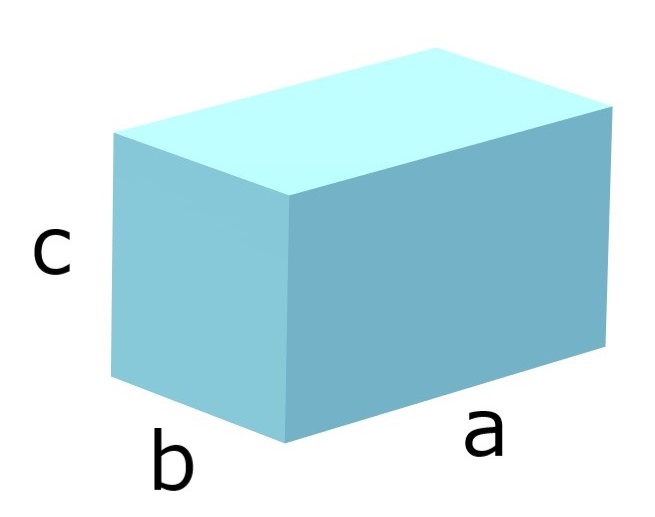
たての長さa、よこの長さb、高さcの直方体を考えます。
(直方体の体積)=(たて)×(よこ)×(高さ)
なので、この直方体の体積はabcです。
かけ算は左から順にかけるので
$$abc=(a\times b)\times c$$
に注意します。
今度は直方体を立ててみます。
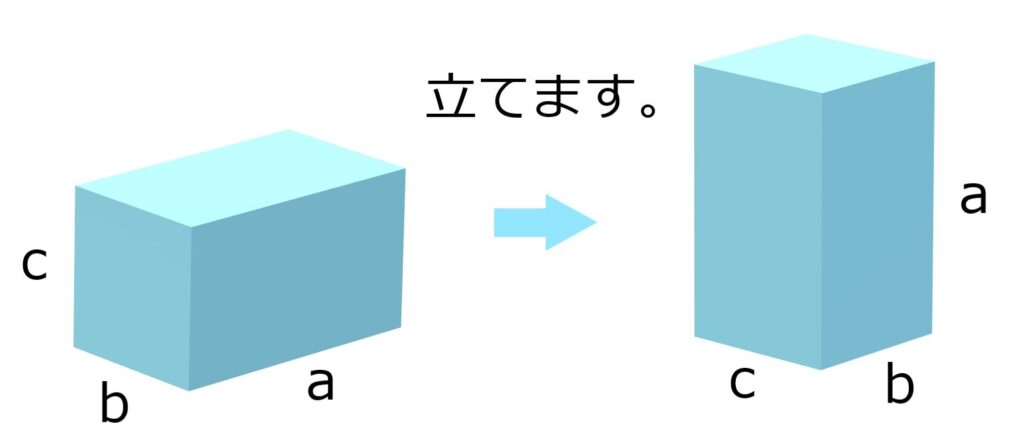
すると、
たての長さb、よこの長さc、高さaになるので
体積はbcaです。
同じく
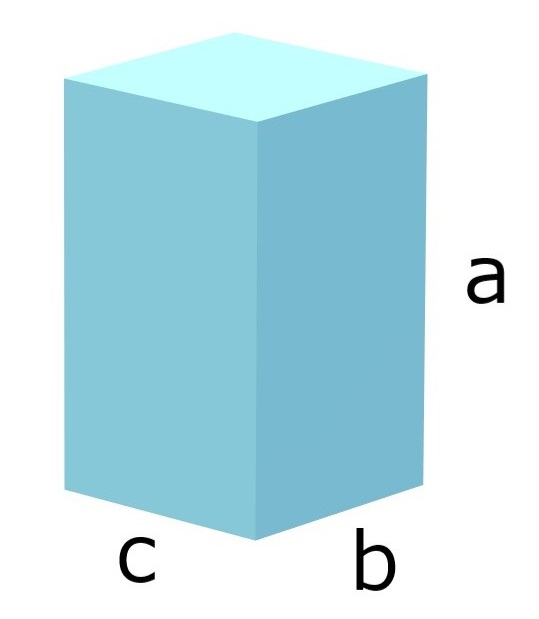
$$bca=(b\times c)\times a$$
です。
直方体の体積は立てる前後で等しいので
$$(a\times b)\times c=(b\times c)\times a$$
を得ます。
最後に乗法の交換法則より右辺を
$$(b\times c)\times a=a\times(b\times c)$$
とできるので
$$(a\times b)\times c=a\times(b\times c)$$
が証明されます。
まとめ
乗法の交換法則・結合法則は、かけ算をする際
「かける順番を換えても良い」
「どこから、かけても良い」
という風に、当たり前に使われていますが証明が必要です。
長方形の面積、直方体の体積を利用すると
簡単に説明できるので、紹介させて頂きました。
