
高校数学の教科書を開くと、くじ引きの確率は
条件つき確率という形で説明されていて、
難しいと感じた人も多いと思います。
ここでは、わかりやすさを重視して、
樹形図を用いた数え上げで
確率を計算する方法を解説します。
(計算すると条件つき確率と同じ計算式に帰着します)
記事の後ろに行くほど難しくなります。
大事なことは始めにすべて書いてあるので、
読める所までで大丈夫です。
くじ引きの確率
くじ引きの確率を計算するには樹形図を書きます。
例えば、くじ箱にabcde

と書かれた5枚の紙の入っている
くじ引きを3回する際の樹形図を書いてみます。

(見やすくするため線は省略してます)
大文字が一回目、中文字が二回目、小文字が三回目です。
ポイントは一度引かれた物は
次のステップで減って行くこと。
枝分かれを考えて、
くじの引かれ方は全部で5×4×3通り、とわかります。
確率の計算方法
それぞれの引かれ方
- a―b―e
- b―d―a
- e―a―c
は名前が異なるだけの同じ物なので、
起きやすさも一緒です。(同様に確からしい根元事象)
具体的に、いくつか計算してみます。
一回目にaを引く確率は?
一回目にaを引く引き方を数えると

1×4×3通り。
これを、くじの引かれ方の総数(5×4×3通り)
で割り算して求める確率は
$$ \frac{1 \times 4 \times 3}{5 \times 4 \times 3 } = \frac{1 }{ 5} \hspace{20cm}$$
です。
一回目にbを引いて三回目にeを引く確率は?
- 一回目にb引いた後
- 二回目にe以外を引いて
- 三回目にeを引く
引き方は1×3×1通り。

これを、くじの引かれ方の総数(5×4×3通り)
で割り算して求める確率は
$$ \frac{1 \times 3 \times 1}{5 \times 4 \times 3 } = \frac{1}{20 } \hspace{20cm}$$
です。
引かれ方の総数
順列の記号Pを用いるなら
くじ箱の中身がn個のくじ引きをr回する際の、
引かれ方の総数は
\( {}_n \mathrm{P}_r \)
と書かれます。
大事な説明は以上です。
求めたい確率についての根元事象を数え上げて、
引かれ方の総数nPrで割り算することが
くじ引きの確率の求め方の基本であり、全てです。
数えれば良いとはいえ、
一個ずつ数えると時間がかかります。
ここからは、頻出の問題を通して
数え上げのテクニックを深めたいと思います。
ab、を当たり、cde、を、はずれ、とします。
みんなで引く確率

2人で引く

Aさんが一回目に、はずれを引き、
Bさんが二回目に当たりを引く確率は?
くじの引かれ方の総数は5×4通り。
Aさんのはずれの引き方はcdeの3通り。
はずれcdeの後には、
どれも当たりabが用意されているので
続くBさんの当りの引き方は2通り。

$$ \frac{3 \times 2 }{5 \times 4 } = \frac{3 }{10 } \hspace{20cm}$$
が答えです。
3人で引く

A、B、Cさんの3人で順番に引くとき
A、Bさんは、はずれを引き、
Cさんは当りを引く確率は?
くじの引かれ方の総数は5×4×3通り。
Aさんのはずれの引き方はcdeの3通り。
続くBさんの、はずれの引き方は、
Aさんの引いた、はずれ以外の2通り。
その後、Cさんには、
2つの当りabが残されているので
注目している根元事象は

3×2×2通り。
$$ \frac{3 \times 2 \times 2 }{5 \times 4 \times 3 } = \frac{1 }{5 } \hspace{20cm}$$
が答えです。
4人で引く

A、B、C、Dさんの4人で順番に引くとき
A、Dさんは当り
B、Cさんは、はずれを引く確率は?
くじの引かれ方の総数は5×4×3×2通り。
- Aさんの当りの引き方は2通り。
- Bさんのはずれの引き方は3通り。
- Cさんのはずれの引き方は、
Bさんの引いたはずれ以外の2通り。 - Dさんの当りの引き方は、
Aさんの引いた当り以外の1通り。
なので根元事象の数は
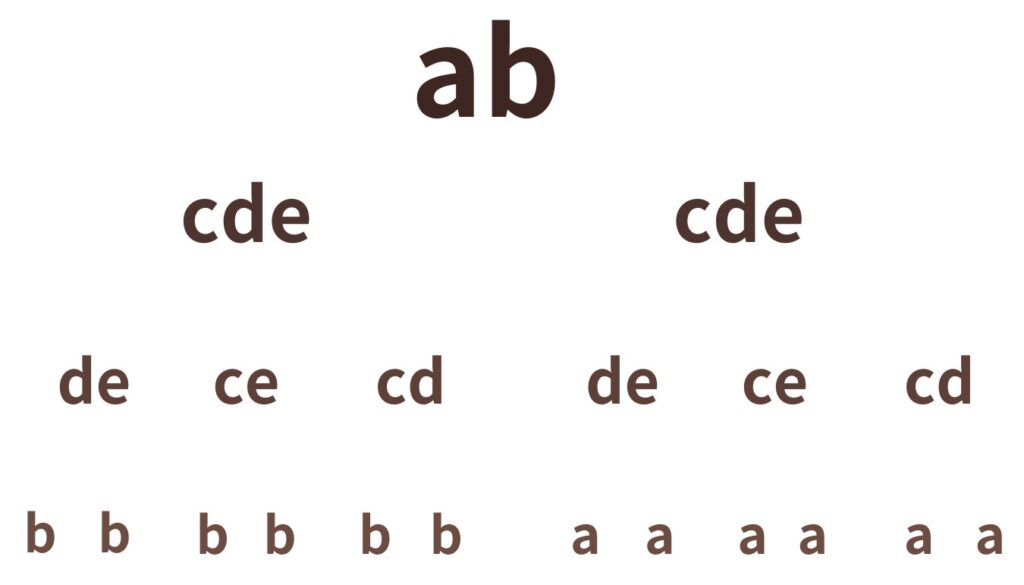
2×3×2×1通り。
$$ \frac{2 \times 3 \times 2 \times 1 }{5 \times 4 \times 3 \times 2 } = \frac{1 }{10 } \hspace{20cm}$$
が答えです。
m人で引くときの公式
ここまでの問題を振り返ると公式が見えてきます。
すなわち全部でn個入っているくじを、
m人で順番に引くとき
当りを引いた人、はずれを引いた人が
指定されているなら求める確率は
m人で引く確率
$$ \frac{ \{x (x-1) (x-2) \cdots \} \{ y (y-1) (y-2) \cdots \} }{ {}_{n} \mathrm{P}_{m} } \hspace{20cm}$$
- x:当りの個数
- y:はずれの個数
です。
…の部分は当りを引いた人の数、
はずれを引いた人の数だけ続きます。
1人で引く


Aさん1人だけで3回くじを引いたとき
当りを引く確率は?
1人で繰り返し、くじを引いて行って
当りを引けるかは気になると思います。
そのまま数えても良いのですが、楽をするために
反対の全てはずれる引き方を数えます。
すなわち
- 一回目にはずれcdeの、どれかを引き
- 二回目に一回目に引いたはずれ以外の
2つのはずれの、どれかを引き - 三回目に余った一つのはずれを引く
引き方は3×2×1通り。
くじの引かれ方の総数は5×4×3通りなので
当りを引く引き方は
(5×4×3)-(3×2×1)通りあります。
$$ \frac{(5 \times 4 \times 3) -(3 \times 2 \times 1 ) }{ 5 \times 4 \times 3} = \frac{54 }{60 } = \frac{9 }{10 } \hspace{20cm}$$
が答えです。
一般の当たる確率
一般にn個のくじの中の当りをx個とし、
くじをr回引くなら全てはずれる引き方は
\( {}_{n-x} \mathrm{P}_{r} \)
通りです。
くじの引かれ方の総数はnPr通りなので、
当る引き方は
$$ {}_n \mathrm{P}_{r} - ({}_{n-x} \mathrm{P}_{r} ) \hspace{20cm}$$
通り、
当たる確率は
当たる確率
$$ \frac{ {}_n \mathrm{P}_{r} - ({}_{n-x} \mathrm{P}_{r} ) }{ {}_n \mathrm{P}_{r}} = 1 - \frac{ {}_{n-x} \mathrm{P}_{r} }{ {}_n \mathrm{P}_{r}} \hspace{20cm}$$
です。
総積記号Πを用いて
$$1 - \prod_{i=0}^{r-1} \frac{ n-x-i }{ n-i} \hspace{20cm}$$
と書けます。
丁度k個当たる確率
先程の当たる確率は、
少なくとも一つ当たりを引く確率と同義です。
丁度一つ当たる確率、丁度二つ当たる確率、…
は次の公式で求まります。
丁度k個当たる確率
$$\frac{ {}_r \mathrm{C}_{k} \, ( {}_{x} \mathrm{P}_{k} \times {}_{n-x} \mathrm{P}_{r-k} ) } { {}_n \mathrm{P}_{r}} \hspace{20cm}$$
総積記号で書くと
$$={}_r \mathrm{C}_{k} \, \left( \prod_{i=0}^{i=k-1} \frac{x-i }{n-i} \right) \left( \prod_{j=0}^{j=r-k-1} \frac{n-x-j }{n-k-j } \right) \hspace{20cm}$$
証明
丁度k個当たる、ということは
引く回数r回のどこかk箇所で当り、
残りのr-k箇所ではずれを引くことを意味します。
そのk箇所の指定の仕方がrCk通り、
指定された引かれ方は、
かけ算の順番を入れ換えることで
共通して各々xPk・n-xPr-k通り
なので、丁度k個当たる引き方は、
rCk(xPk・n-xPr-k)通りあります。\( \square \)
かけ算の順番を入れ換えるテクニックは、
m人で引く確率でも使いました。
少なくともℓ個当たる確率
少なくとも一つ当たる確率(当たる確率)から
丁度1個当たる確率を引き算すると、
少なくとも二つ当たる確率を求められます。
$$ \left( 1 - \frac{ {}_{n-x} \mathrm{P}_{r} }{ {}_n \mathrm{P}_{r}} \right) - \frac{ {}_r \mathrm{C}_{1} \, ( {}_{x} \mathrm{P}_{1} \times {}_{n-x} \mathrm{P}_{r-1} ) } { {}_n \mathrm{P}_{r}} \hspace{20cm}$$
続けて、少なくとも三つ当たる確率
$$ \left( 1 - \frac{ {}_{n-x} \mathrm{P}_{r} }{ {}_n \mathrm{P}_{r}} \right) - \frac{ {}_r \mathrm{C}_{1} \, ( {}_{x} \mathrm{P}_{1} \times {}_{n-x} \mathrm{P}_{r-1} ) } { {}_n \mathrm{P}_{r}} - \frac{ {}_r \mathrm{C}_{2} \, ( {}_{x} \mathrm{P}_{2} \times {}_{n-x} \mathrm{P}_{r-2} ) } { {}_n \mathrm{P}_{r}} \hspace{20cm}$$
も求まります。
一般に、少なくともℓ個当たる確率は
$$ \left( 1 - \frac{ {}_{n-x} \mathrm{P}_{r} }{ {}_n \mathrm{P}_{r}} \right) -\sum_{k=1}^{l-1} \frac{ {}_r \mathrm{C}_{k} \, ( {}_{x} \mathrm{P}_{k} \times {}_{n-x} \mathrm{P}_{r-k} ) } { {}_n \mathrm{P}_{r}} \hspace{20cm}$$
これは
少なくともℓ個当たる確率
$$1 -\sum_{k=0}^{l-1} \frac{ {}_r \mathrm{C}_{k} \, ( {}_{x} \mathrm{P}_{k} \times {}_{n-x} \mathrm{P}_{r-k} ) } { {}_n \mathrm{P}_{r}} \hspace{20cm}$$
と書けます。
\( ( {}_r \mathrm{C}_{0} = {}_x \mathrm{P}_{0} = 1 ) \)
何個以上当たれば満足かを考える時に便利です。
余談
関連して純粋数学の綺麗な公式があるので紹介します。
n個のくじの中の当りの個数をxとし
くじをr回引くなら結果は明らかに、
引いた当りの個数が丁度0~r個のいずれかです。
起きうるすべての事象の確率の総和は1なので、
n, x, r(n≧x, r)を自然数として
純粋数学の公式
$$\sum_{k=0}^{r} \frac{ {}_r \mathrm{C}_{k} \, ( {}_{x} \mathrm{P}_{k} \times {}_{n-x} \mathrm{P}_{r-k} ) } { {}_n \mathrm{P}_{r}} = 1 \hspace{20cm}$$
が成り立ちます。
複雑な左辺をすべて足すと必ず1になる、
という純粋数学的に綺麗な公式です。
順列Pの定義
ここまでの公式を扱う際は順列
\( {}_\alpha \mathrm{P}_\beta \)
の定義を
- α=β=0の時は1
- α<βの時は0
により拡張すると都合が良いです。
一つ目の定義はくじの中身がすべて当りの時
二つ目の定義は当りk個、はずれr-k個の引き方が
くじの中の当り、はずれの個数不足で不可能な時、
計算結果を合わせてくれます。
まとめ
くじ引きの確率計算には樹形図を書きます。
基本は注目している根元事象を数えて、
くじの引かれ方の総数nPrで割り算すること。
数え上げのテクニックは色々あるものの
引いたくじが一つずつ減って行くのに合わせた
かけ算で大体の問題は解けます。
