
高校で勉強する正弦定理と余弦定理は、
sinとcosの複雑な式で
日常生活の何の役に立つのか疑問だと思います。
実はこの二つの定理は測量という形で
とても身近に使われています。
私たちの便利な暮らしは
距離、角度を正確に測ることの上に成り立っているので、
重要な定理と言えます。
この記事では、正弦定理と余弦定理が
三角測量と呼ばれる技法の要であること、
具体的にどのような仕事に利用されているか、まで説明します。
正弦定理と余弦定理の使い道
私たちの生活における、
正弦定理と余弦定理の使い道は三角測量です。
三角測量とは三角形を描いて、
特に、直接測定が難しい大規模な地形の距離や、
天体の位置を算出する技法のことです。

東京から大阪までの距離は?
地球から月までの距離は?

手作業で測れるのは、
数kmあたりが限界なので工夫が要ります。
三角測量の応用
三角測量は近代から現代に至るまで、
例えば以下の仕事に利用されて来ました。
- 地図作成
- 建設
- 天文学
- GPS技術
三角測量の基本原理
なぜ、三角測量で長距離を測れるかと言うと、
角度の測定が距離の測定より容易なためです。
具体的には次の原理によります。
基線の測定
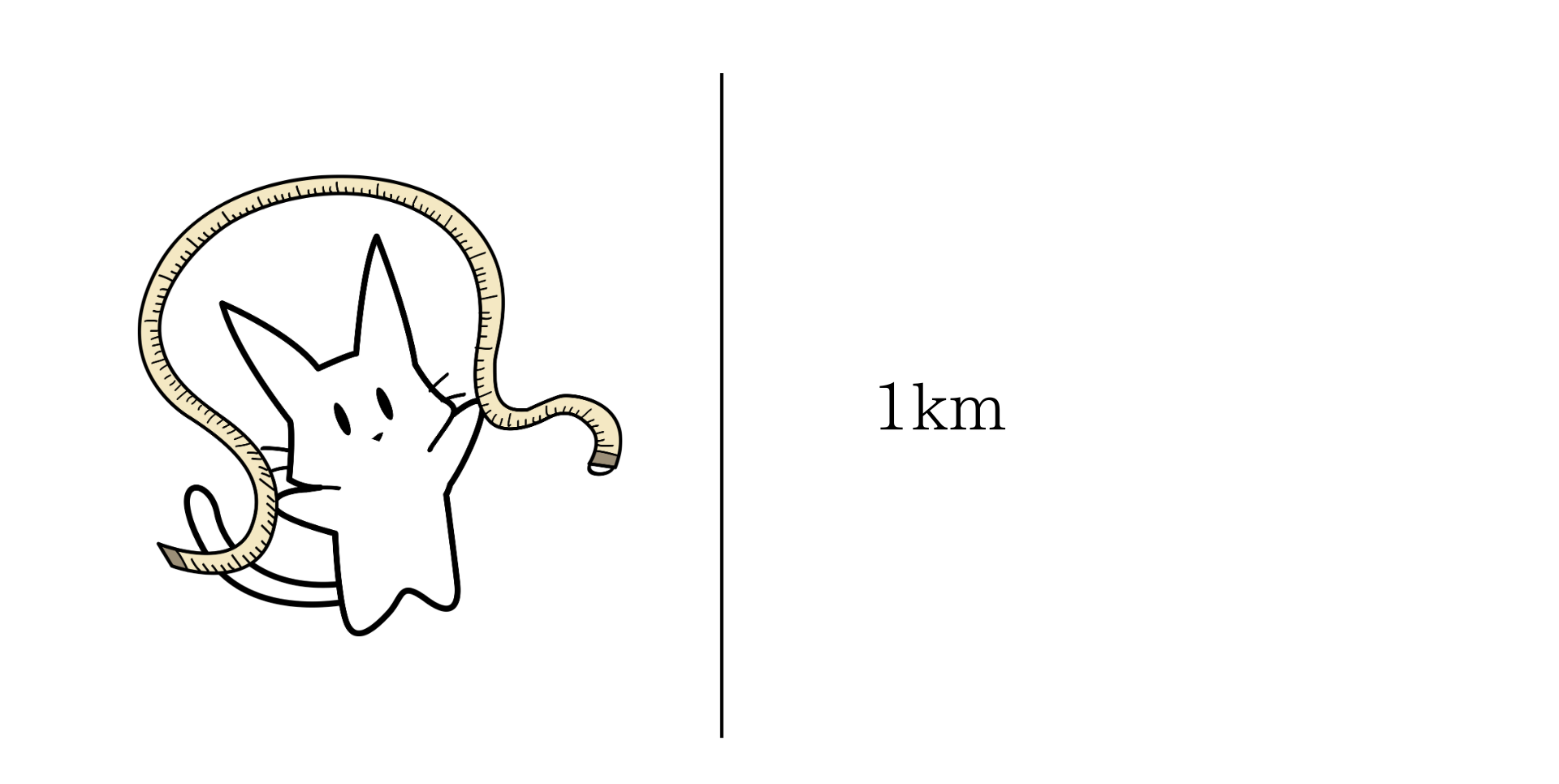
始めに、計算の基となる線(基線)を直接測定します。
これが三角形の底辺となります。
角度の測定
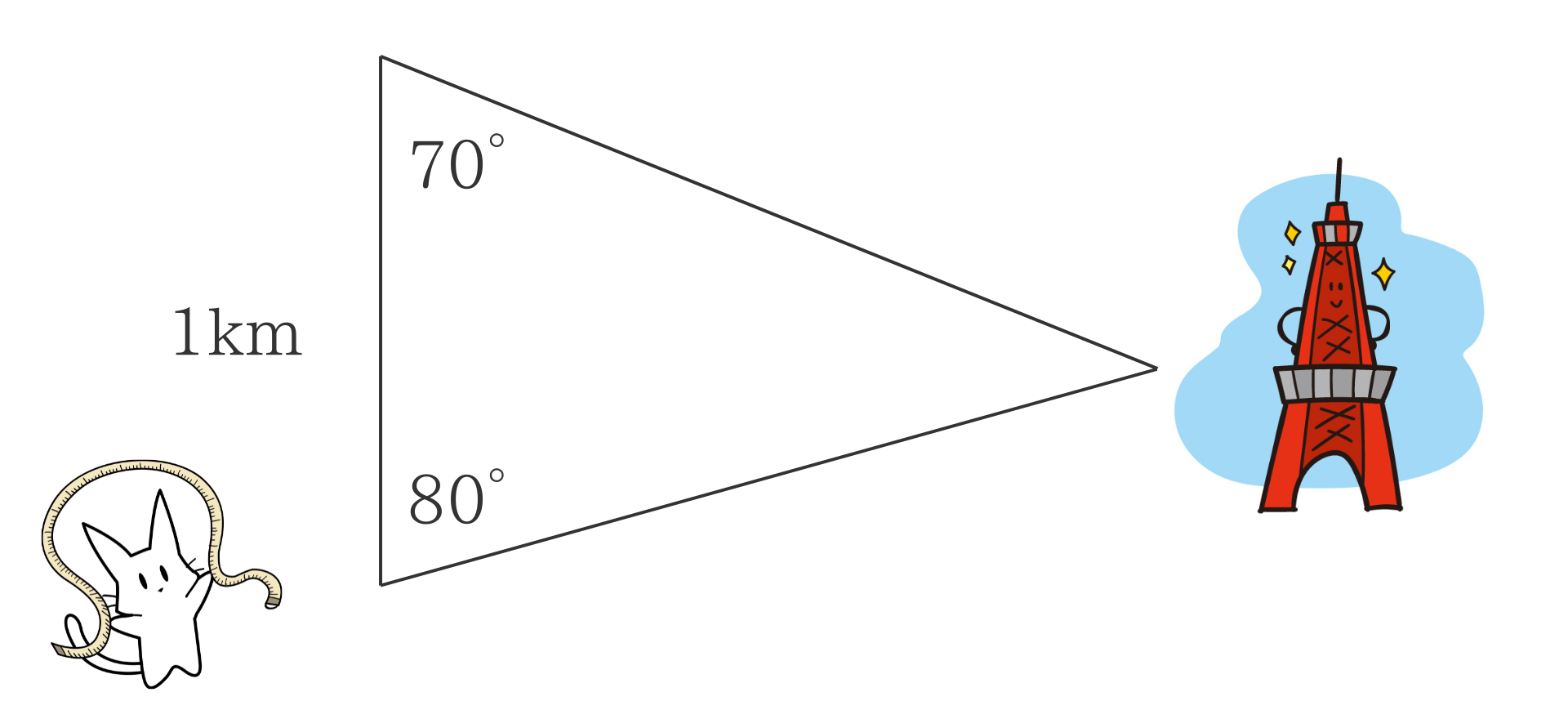
次に、基線の両端から目的地への角度を測定します。
この角度をどれだけ正確に測れるかが大事です。
三角形の計算
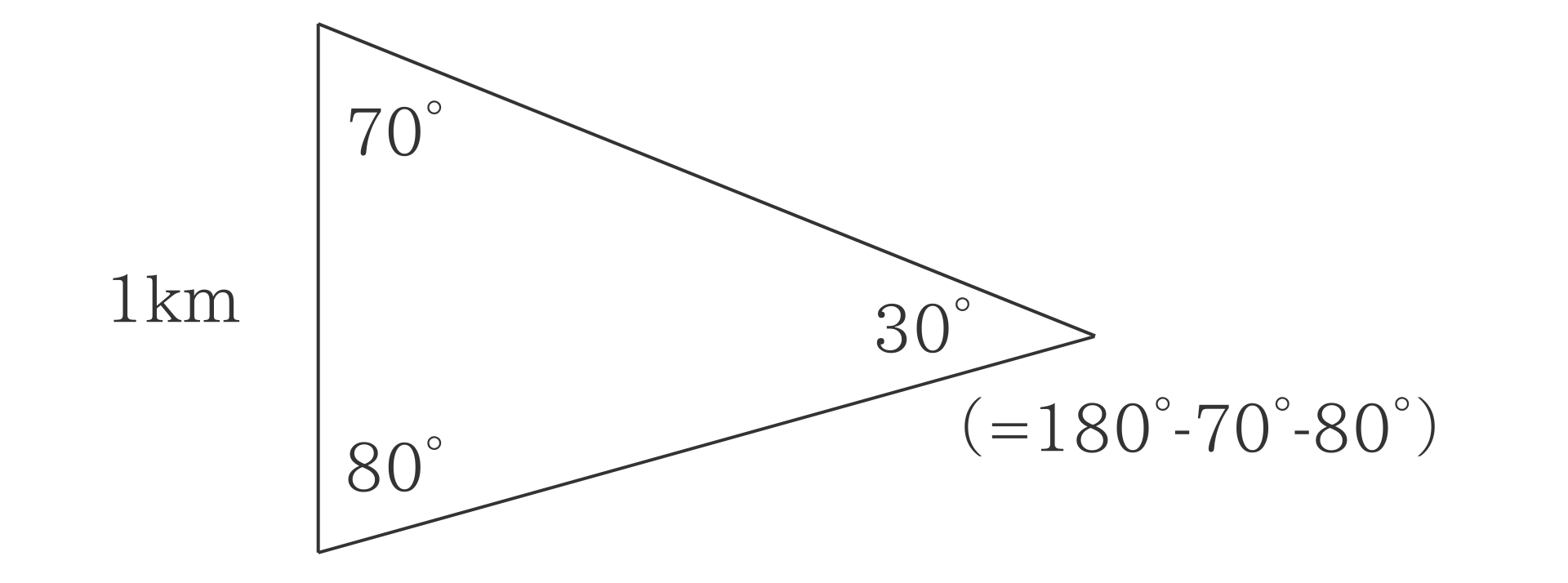
基線と測定した角度を用いて、正弦定理を適用します。
基線よりずっと長い三角形の斜辺の長さが求まりました。
地図作成
広範囲にわたる地図を正確に描けます。
明治時代の日本地図は三角測量で作られました。
建設

大規模な建設計画において、建物の構造、地形を
正確に把握するため使用されます。
特に、橋梁や高層ビルの建設において重要です。
天文学
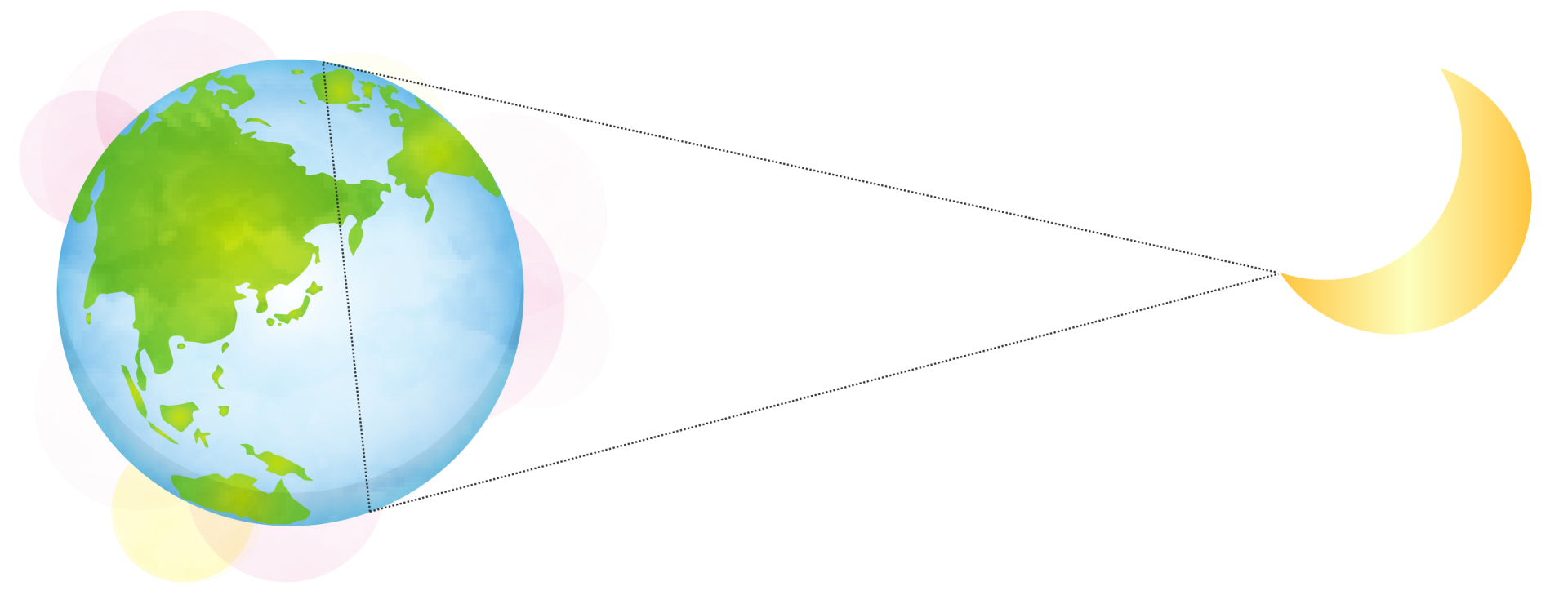
天体の位置を直接測定することは不可能です。
例えば地球から月までの距離を測定するには、
地球上の異なる2点から同時に観測を行います。
三角法
三角測量に用いられる理論を、まとめて三角法と呼びます。
三角法と聞くと難しく感じますが、
要は正弦定理と余弦定理のことです。
復習すると、
正弦定理
$$ \frac{a}{\sin \mathrm{A} } = \frac{b}{\sin \mathrm{B} } = \frac{c}{\sin \mathrm{C} } \hspace{20cm}$$
三角形の2辺と、2角の内、
3つが求まっていれば残りの1つも求まります。
例題
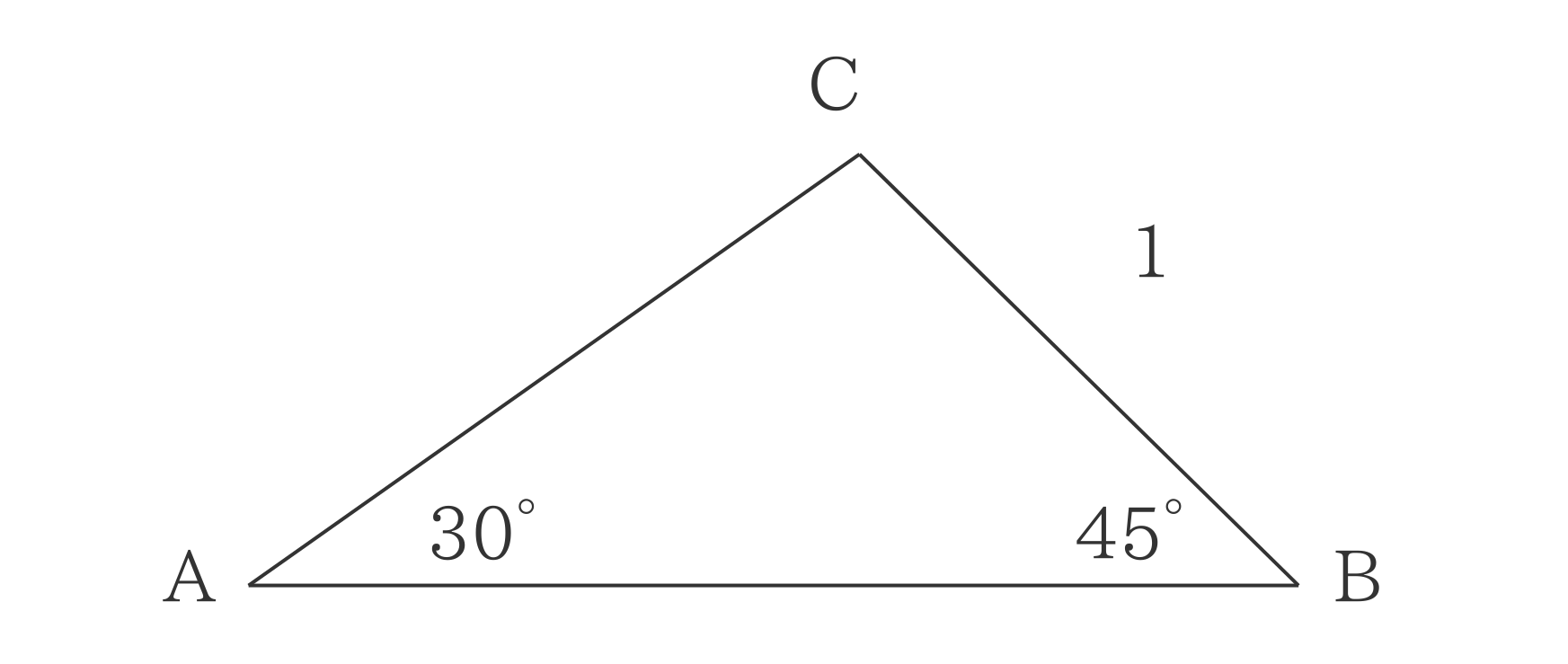
∠A=30°、∠B=45°、a=1、と測定できているなら
$$ \frac{a}{\sin \mathrm{A} } = \frac{b}{\sin \mathrm{B} } \hspace{20cm}$$
$$ 1 \cdot 2 = b \cdot \sqrt{2} \hspace{20cm}$$
よりb=√2と求まります。
余弦定理
$$ c^2 = a^2 +b^2 -2ab \cos \mathrm{C} \hspace{20cm}$$
三角形の3辺と、1角の内、
3つが求まっていれば残りの1つも求まります。
例題
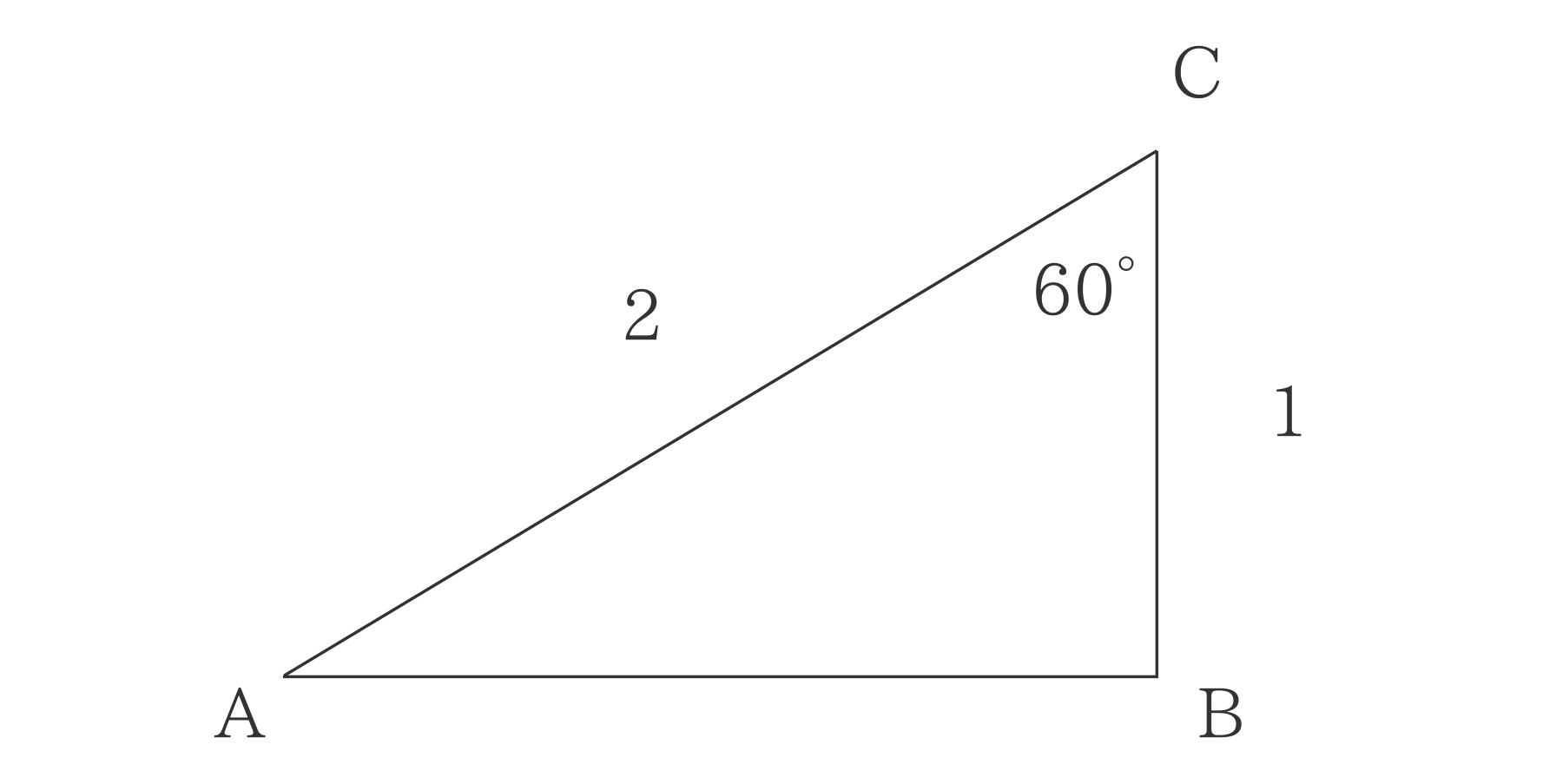
a=1、b=2、∠C=60°、と測定できているなら
$$ c^2 = 1^2 +2^2 -2 \cdot 1 \cdot 2 \cdot \frac{1}{2} \hspace{20cm}$$
$$ c^2 = 1 +4 -2 \hspace{20cm}$$
よりc=√3と求まります。
三角形は3つの辺と、3つの角度を持つので、
合計で6つ測定すべき箇所があります。
これらの内の3つが測定できていれば
正弦定理と余弦定理を繰り返し用いることで、
残りの4つ目、5つ目、6つ目も
芋づる式に求められる、そんな理論となってます。
GPS技術
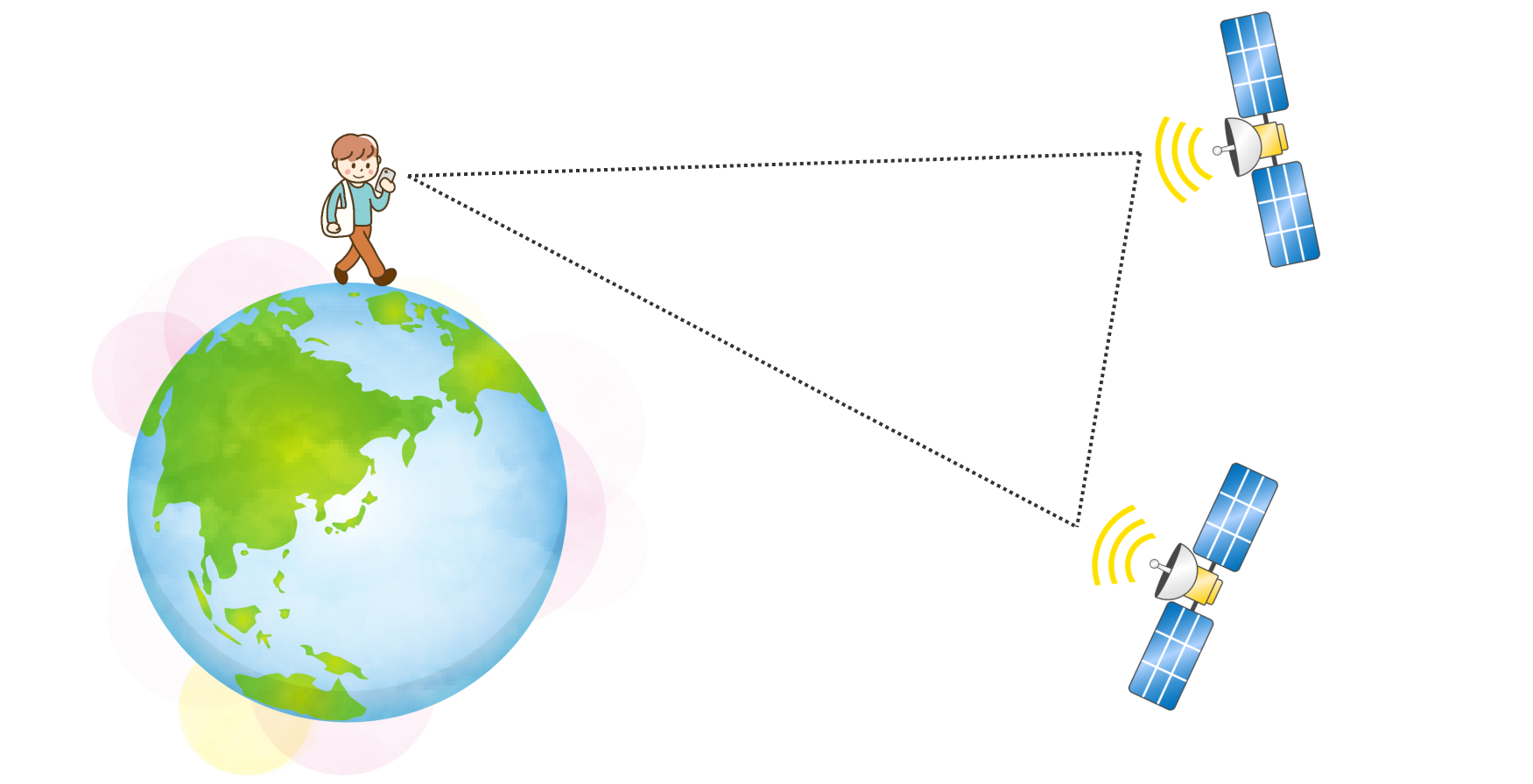
三角測量の現代における極めつけは、
位置情報サービスのGPSです。
歩行者、車、船、飛行機の道案内。
果ては遭難救助まで幅広く用いられる重要な技術です。
位置の分かっている衛星から、端末まで電波を飛ばして、
電波が届くまでの時間から距離を測ります。
これは、3辺の長さが求まっている場合の三角法になります。
まとめ
正弦定理と余弦定理は、三角測量として、
私たちの便利な暮らしを支えてくれています。
三角測量とは測定したい3地点を結んで、三角形を描いて、
知りたい距離、角度の情報を計算で求める手法です。
三角測量の基本原理を理解することで、
これらの技術の背後にある
科学的な原理をより深く理解することができます。
