
指数関数的に増加、の反対の意味の
指数関数的に減少(減衰)を
理系院卒の私がわかりやすく説明します。
指数関数的に減少(減衰)とは
指数関数的に減少(減衰)とは
指数関数
$$ y = \left( \frac{1}{2} \right)^x \hspace{20cm} $$
のグラフのように
最初は勢いよく、次第にじりじりと
0に向かい減って行くことを意味します。
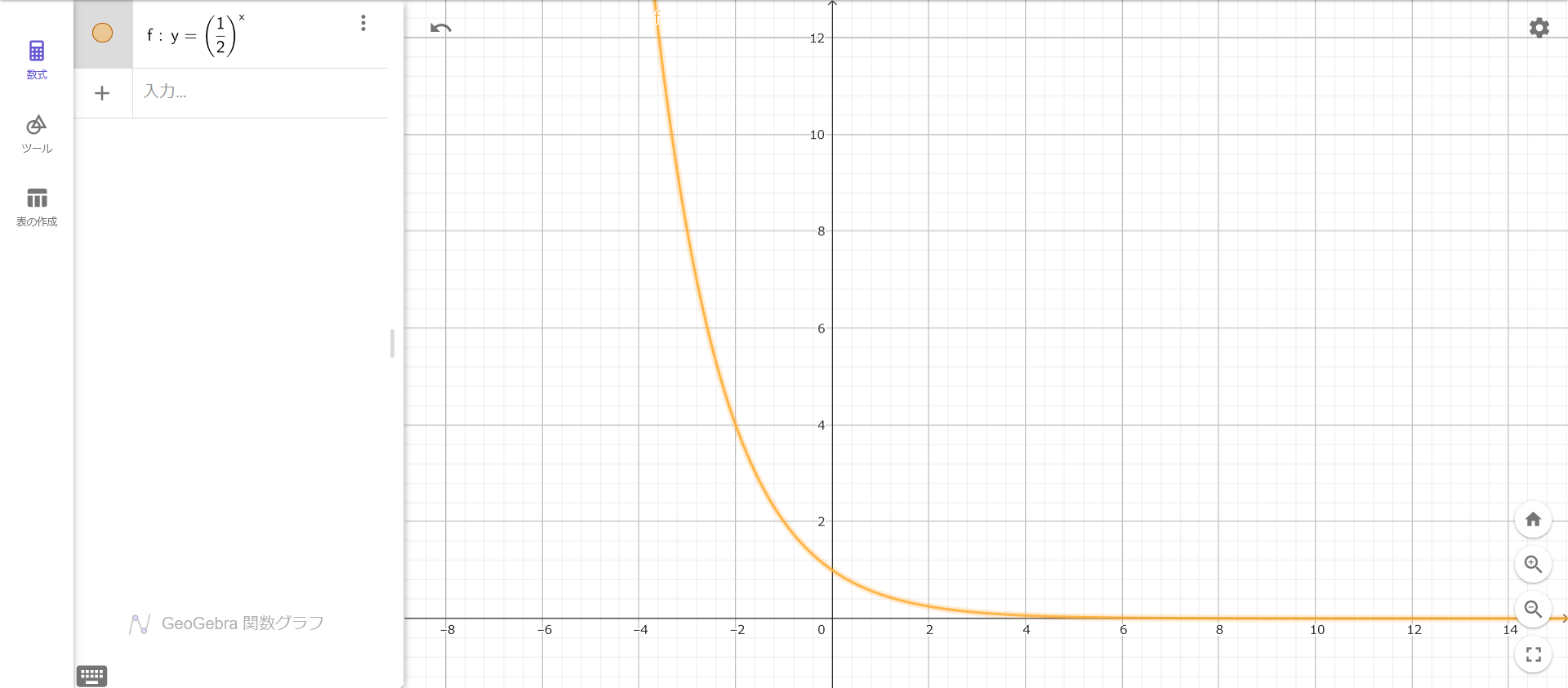
略して指数的減衰とも言われます。
数式で定義するなら、0<a<1として
\( y = a^x \)
のグラフがこの言葉を表します。
具体例はこちら
減少vs減衰
科学者の間では指数関数的に減衰の方がよく使われます。
これは0に限りなく近づくけど
0にはならない様に対し
減り衰えるがより精確な表現のためです。
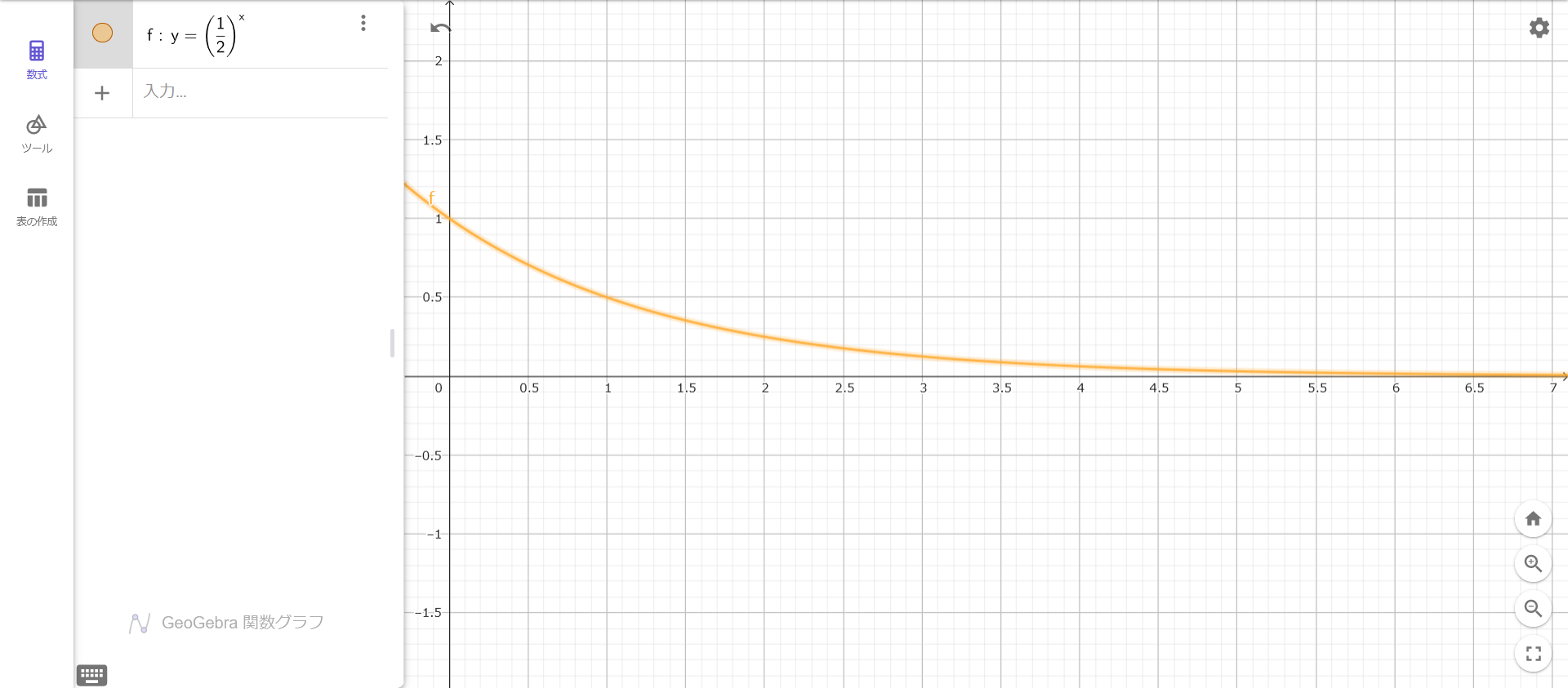
指数関数的に減少でも意味は通じます。
減少には
\( y = -x \)
のように
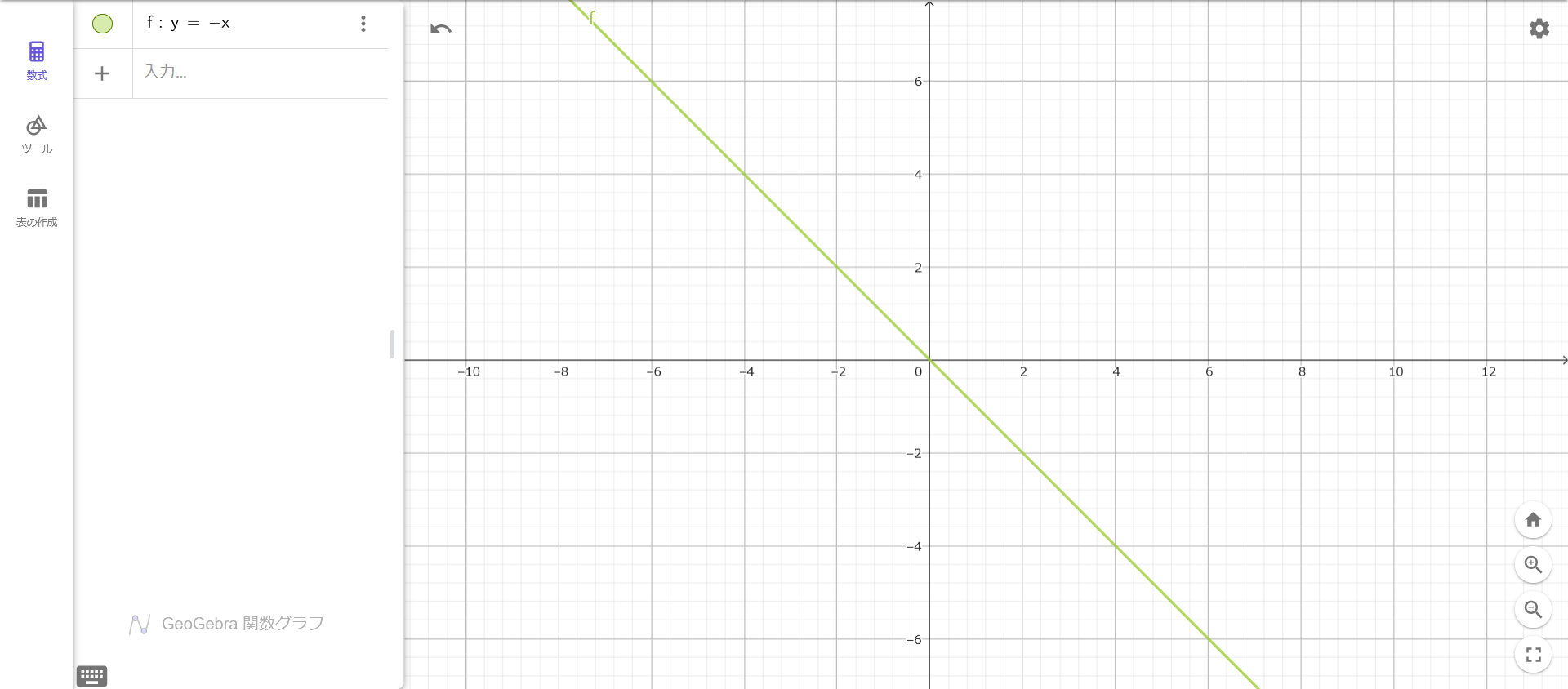
0を通り越して負の数まで行くイメージがあります。
余談
微分方程式による理解
微分方程式という分野から
見た場合の定義を載せておきます。
意味する所は同じです。
定義
時間によって変化する数N(t)の変化量が
常に自身N(t)の負の定数-λ倍
すなわち方程式
$$ \frac{dN(t) }{dt } = -\lambda N(t) \hspace{20cm} $$
を満たすときN(t)は
指数関数的に減少(減衰)していると言う。
指数関数的に増加

ちなみに
\( y = a^x \)
において1<aの時が指数関数的に増加です。
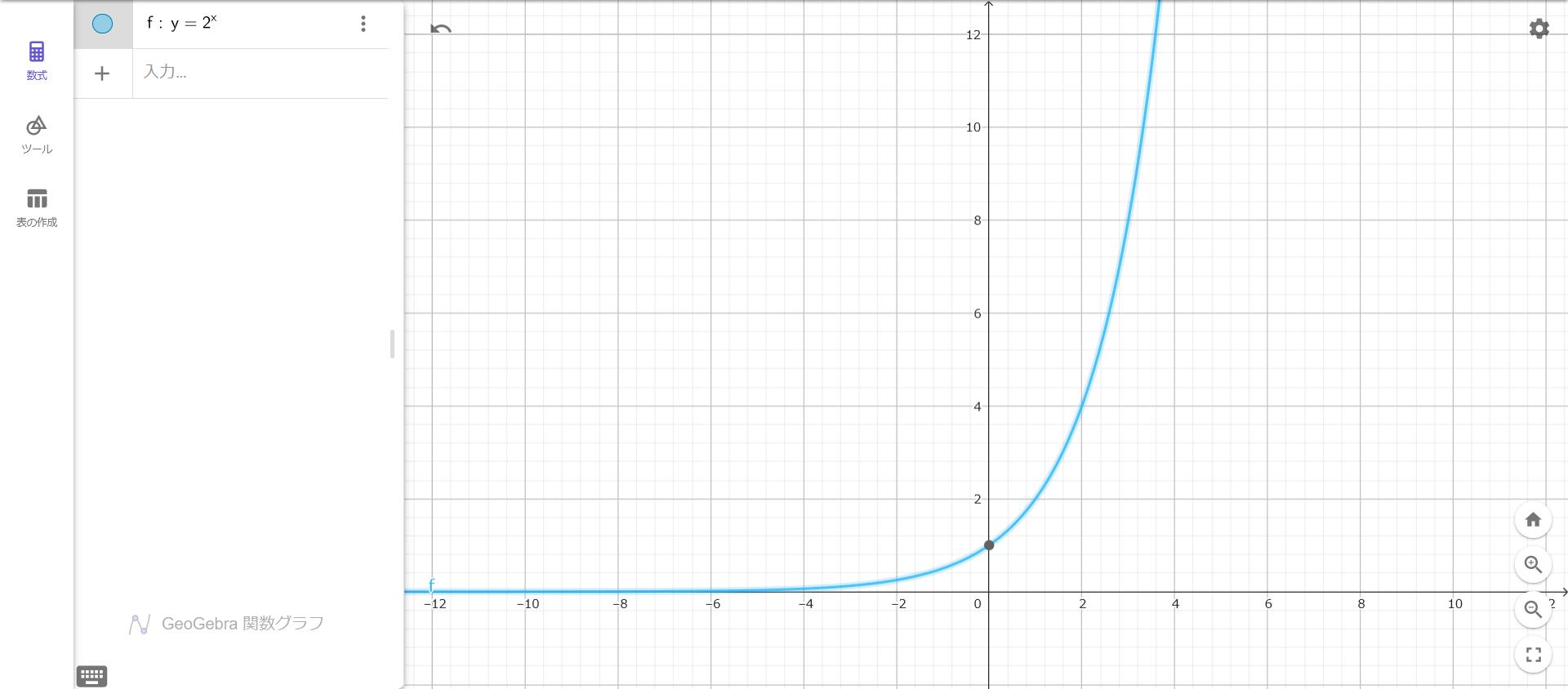
まとめ
指数関数的に減少(減衰)とは
最初は勢いよく、次第にじりじりと
0に向かい減って行くことを意味します。
減少より減衰の方が学術的に好まれます。

