x2、sinx、等を見ていると
関数が実数全体を定義域に持つ事は
当然に感じられると思います。
指数関数axは特殊で、始めは
xが自然数の時のみ値を持ちます。
この記事では
xが自然数でない時について
累乗の定義のされ方と理由、
指数関数の逆として対数関数が生まれ
最終的に指数が複素数まで拡張し得る所まで。
指数関数の導出過程をまとめます。
指数関数の出発点
指数関数は累乗(べき乗)から始まります。
累乗とは何かと言うと、
同じ数aを自然数n回
掛け合わせる計算の事です。
$$\underbrace{ a \times a \times \cdots \times a}_{n個} \hspace{20cm}$$
をanと書きaのn乗、nはその指数と呼ばれます。
指数nが自然数以外の時にも累乗を定義して
実数上の関数を作ろう、
というのが出発点です。
定義の要は指数法則
実数a、bと自然数m、nについて
累乗は3つの指数法則を満たします。
指数法則
- \( a^m a^n = a^{m+n} \)
- \( (a^m)^n = a^{mn} \)
- \( (ab)^n = a^n b^n \)
nが0や負の数の時を定義するに当たり、

aを0回掛ける。
aをマイナス回掛ける。

は意味が良く分かりません。
そこで昔の数学者たちは、
指数法則が保たれる
適当な値を定義として採用しました。
指数の拡張
0乗
一番目の指数法則においてn=0とすれば
$$\quad \, a^m a^0 = a^{m+0} \hspace{20cm}$$
$$\Leftrightarrow a^m a^0 = a^m \hspace{20cm} $$
なので等式を満たすため
0乗の定義
\( a^0 := 1 \)
と定めます。
マイナス乗
自然数nについて一番目の指数法則は
$$\quad \, a^n a^{-n} = a^{n-n} \hspace{20cm} $$
$$\Leftrightarrow a^n a^{-n} = a^0 \hspace{20cm}$$
$$\Leftrightarrow a^n a^{-n} = 1 \hspace{20cm}$$
なので等式を満たすため
マイナス乗の定義
$$ a^{-n} := \frac{1}{a^n} \hspace{20cm} $$
と定めます。
分母にanを使うのでa=0だと都合が悪いです。
この時点でa≠0が仮定に追加されます。
整数乗まで定義
\( a \neq 0 \)
に対して整数まで指数を拡張できました。
この定義は一番目のみならず、
指数法則をすべて満たします。
1/n乗
自然数nについて二番目の指数法則は
\(\quad \, (a^{1/n})^n = a^{(1/n)\times n} \)
\(\Leftrightarrow (a^{1/n})^n = a^1 \)
\(\Leftrightarrow (a^{1/n})^n = a \)
なので
\( x^n = a \)
を満たす数xでaの1/n乗を定めて行きます。
xはn乗根と呼ばれ、
複素数を含めn個存在します。
nが奇数
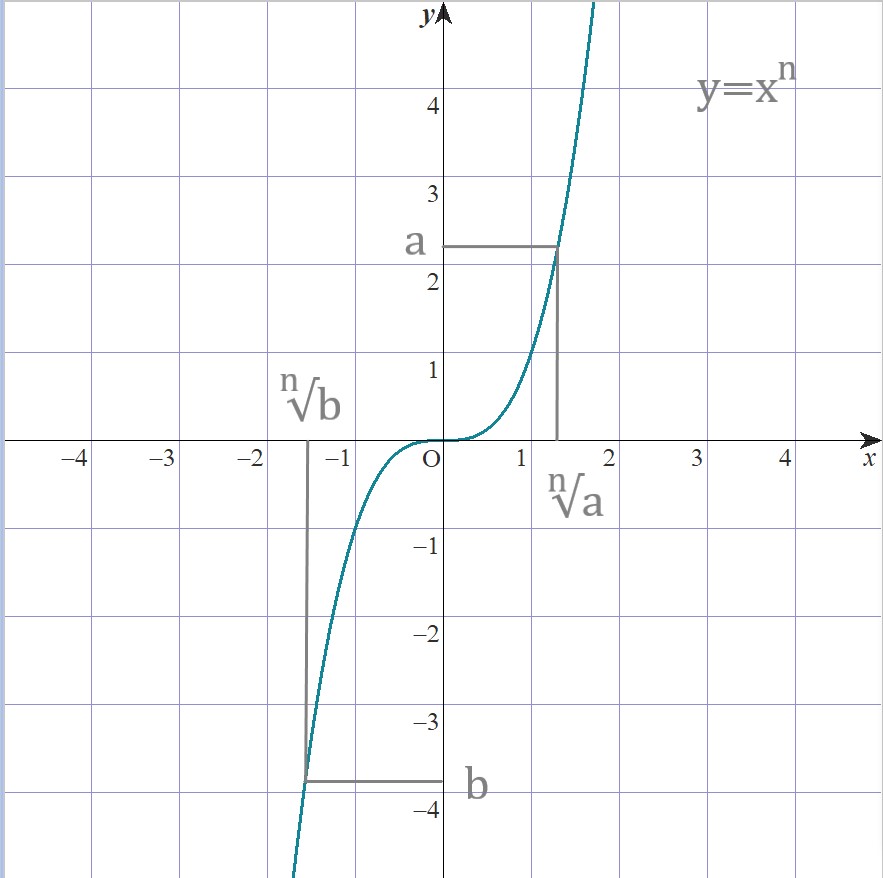
nを奇数とするなら関数y=xnは
-∞から+∞まで単調増加するので、
すべての正の数a、負の数bについて
実数のn乗根は唯一つです。
nが偶数
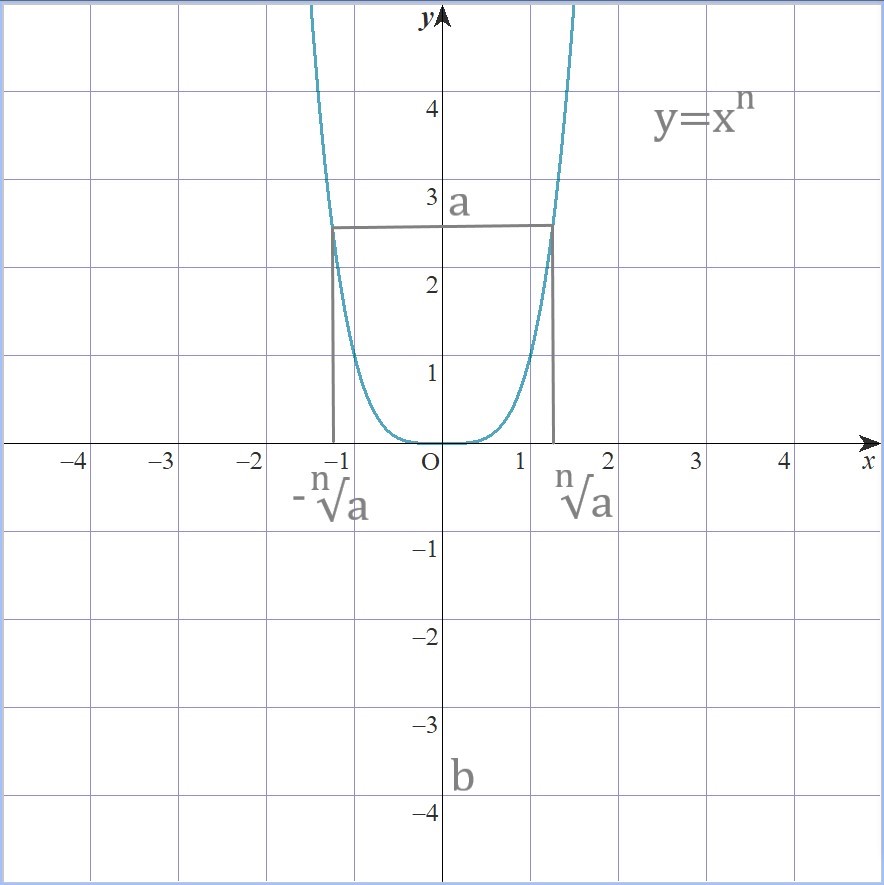
一方、nが偶数ならy=xnは
常に0以上の値をとる偶関数なので
正の数aのn乗根は二つある傍ら、
負の数bのn乗根は実数において存在しません。
従いa>0についてのみ定義します。
aのn乗根の内、
正の値をaの1/n乗に採用します。
1/n乗の定義
\( a^{1/n} := x \)
\( ( x^n = a, \quad x > 0) \)
\( \sqrt[n]{a} \quad (= a^{1/n} ) \)
とも書かれます。
有理数乗
自然数m、nについて二番目の指数法則は
\(\quad \, (a^{m/n})^n = a^{(m/n)\times n} \)
\(\Leftrightarrow (a^{m/n})^n = a^m \)
なので等式を満たすためam/nをamの1/n乗と定めます。
正の有理数乗の定義
\( a^{m/n} := (a^m)^{1/n} \quad (=\sqrt[n]{a^m}) \)
また一番目の指数法則は
\( \quad \, a^{m/n} a^{-m/n} = a^{(m/n) -(m/n)} \)
\( \Leftrightarrow a^{m/n} a^{-m/n} = a^0 \)
\( \Leftrightarrow a^{m/n} a^{-m/n} = 1 \)
なので等式を満たすため
負の有理数乗の定義
$$ a^{-m/n} := \frac{1}{a^{m/n}} \quad (=\sqrt[n]{a^{-m}}) \hspace{20cm} $$
と定めます。
有理数乗の指数法則の証明
\( a>0 \)
に対して有理数まで指数を拡張できました。
この定義は指数法則をすべて満たします。
無理数乗
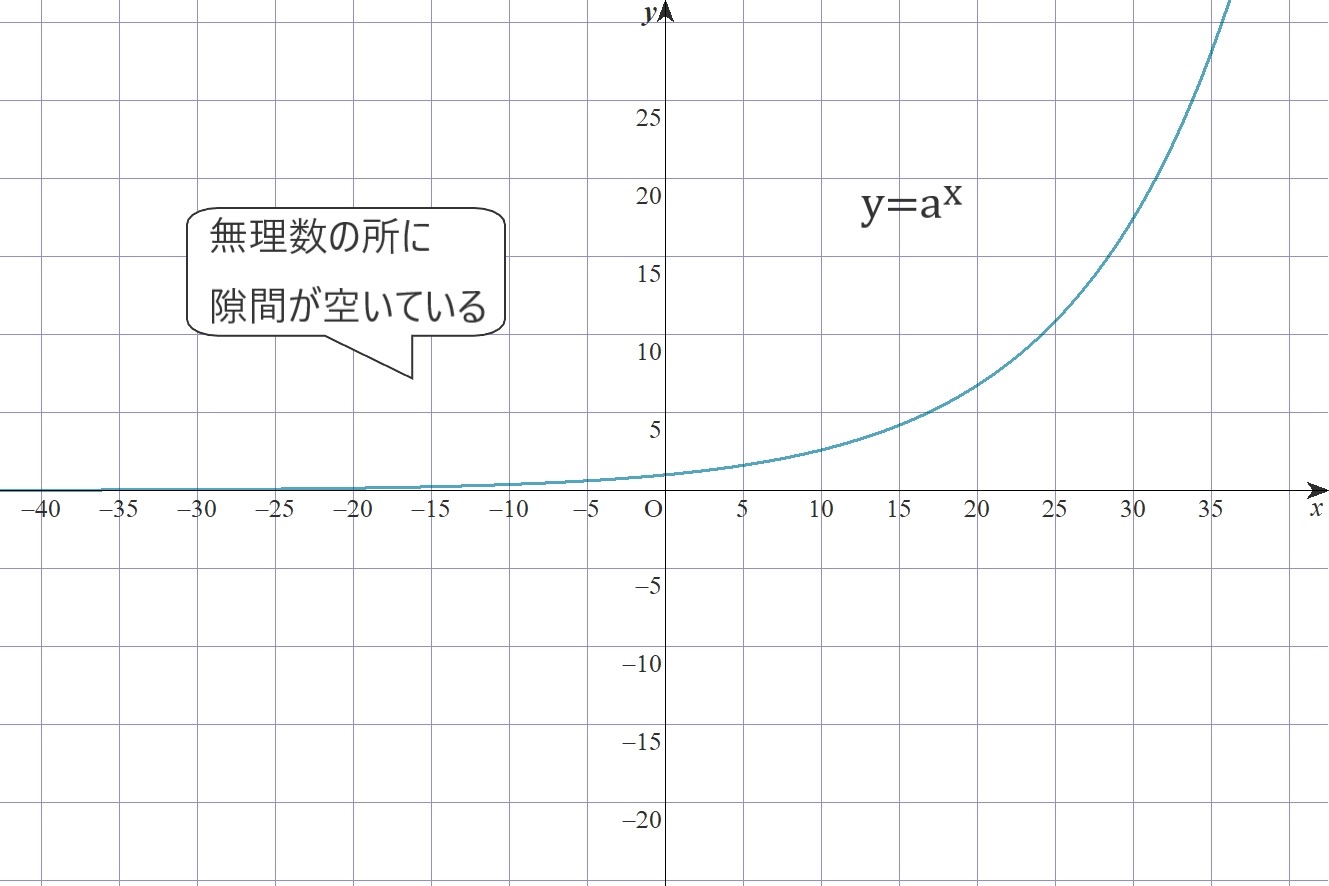
xが有理数の点だけ
y=axのグラフを書いてみると、
少しずつ増えて行く
滑らかな関数に見えます。
なので隙間を埋める様に無理数x乗を定義します。
実数a>0について
無理数乗の定義(高校数学)
\( a^x := \lim_{n \to \infty} a^{r_n} \)
ここで{rn}は
\( \lim_{n \to \infty} r_n = x \)
を満たす任意の有理数列。
大学数学の定義
上の定義は数列が収束する事を
前提にしているので曖昧さがあります。
数列は収束しない事もあります。

大学の講義では、より正確に定義して
指数関数の連続性を示します。
実数乗の指数法則の証明
無理数乗の定義を以って
\( a>0 \)
に対して実数全体で累乗を定義できました。
指数法則が満たされます。
対数関数
指数関数の逆関数もあると便利です。
a>1の場合
axは単調増加かつ連続、
$$\left\{ \begin{eqnarray} \lim_{n \to \infty} a^n &=& \infty \\ \lim_{n \to \infty} a^{-n} &=& \lim_{n \to \infty} \frac{1}{a^n} = \frac{1}{\infty} = 0 \end{eqnarray} \right. \hspace{20cm}$$
より値域は(0, ∞)なので
定義域x>0の逆関数が存在します。
これを対数関数と呼びます。
\( y = \log_a x \quad (x>0) \)
0<a<1の場合
axは単調減少で連続、
$$\left\{ \begin{eqnarray} \lim_{n \to \infty} a^n &=& 0 \\ \lim_{n \to \infty} a^{-n} &=& \lim_{n \to \infty} \frac{1}{a^n} = \frac{1}{0} = \infty \end{eqnarray} \right. \hspace{20cm}$$
より値域は(0, ∞)、 同様に存在します。
a≠1を付ける理由
a=1の場合は逆関数を作れません。
指数関数の底の条件a≠1は
\( y = 1^x \)
が自明な事もありますが
対数関数を持つ際に必要だからです。
実数の指数関数
\( a>0, \quad a \neq 1 \)
に対して逆関数込みで指数関数を定義できました。
複素数の指数関数
実数から足を伸ばして
複素数の指数関数も考えられています。
複素数の指数関数には
一価と多価の物があり、各々
複素数a≠0、任意の複素数zに対し
複素数の指数関数(一価)
$$ a^z := e^{z(\log |a| +i\, \mathrm{Arg} \, a)} \hspace{20cm}$$
複素数の指数関数(多価)
$$ a^z := e^{z(\log |a| +i\, \mathrm{arg} \, a)} \hspace{20cm}$$
の様に定義されます。
Arg a、arg a、で異なります。
指数法則の限界
複素数を使える代わりに
指数法則が崩れてしまいます。
すなわち
一価の複素数の指数関数は
一番目の指数法則のみを満たし、
多価の複素数の指数関数は
三番目の指数法則のみ満たします。
残りの法則は、
部分的に成立したり
完全に不成立と込み入ってます。
まとめ
指数関数axは
始めはxが自然数の時のみ値を持ちます。
残りの値を指数法則を守る様に定めると、
実数全体で連続(実は微分可能)な
綺麗な関数が出来上がります。
これは物理学においては微分方程式、
生物学においては細菌の個体数を
研究するのに便利な物です。
加えて単調増加な事もあり
逆関数として対数関数も作れ、
実数内では大成功と言えます。
複素数まで欲張ってしまうと、
指数法則が崩れてしまい
多価関数だったりで
上手く行かなくなって来ます…。
複素数でも綺麗な
指数関数の新しい定義があれば、と思います。





