
円周角
扇形OABとOCDは中心角が等しい時、
回転させると重なり合う。
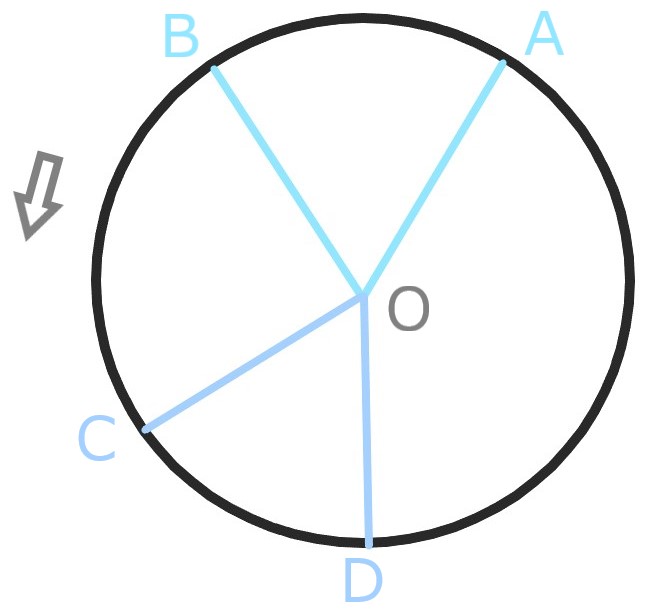
また弧ABとCDの長さが等しくても
同様に重なるので、
さらに
長さの等しい弧に対する弦の長さは等しい。
逆に弦ABの垂直二等分線は円の中心Oを通る。
証明
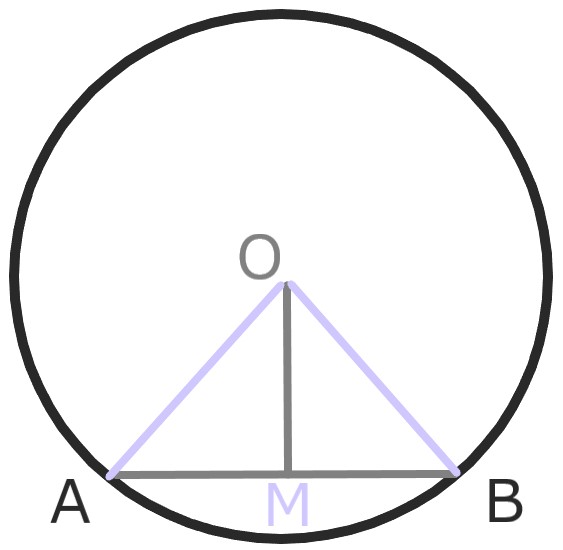
中心Oから弦ABに垂線OMを降ろす。
OAとOBは共に円Oの半径なので、
OA=OB
2組の辺の等しい直角三角形なので
△OMA≡△OMB
となり、AM=BM
OMは弦ABを二等分する。
逆に弦ABの垂直二等分線は
OMと一致するので中心Oを通る。\(\square\)
異なる3点A、B、Pについて次は同値
- ∠APB=90°
- 点PはABを直径とする円周上にある
証明
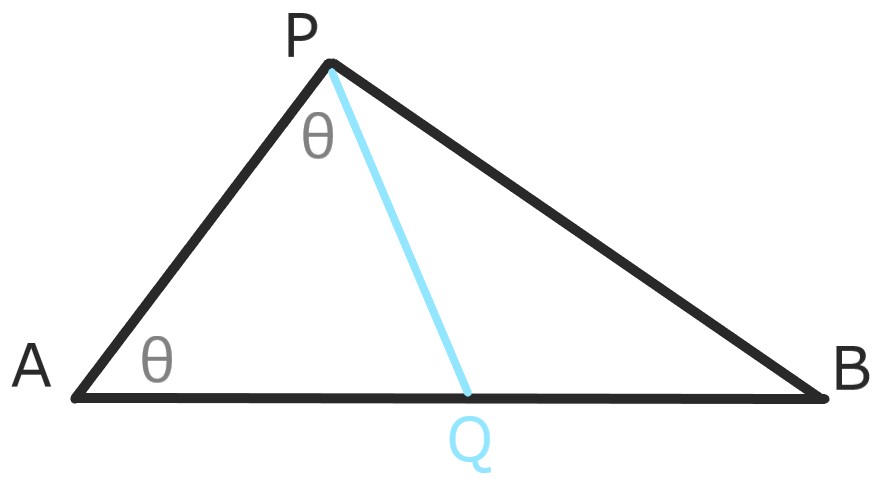
△ABPにおいて∠APB=90°とする。
∠PAB=θとして、
点Pから辺ABに∠APQ=θ
となる様に補助線PQを引く。
△APQは二等辺三角形なのでQA=QP
また、
∠QPB=90-θ
∠QBP=180-90-θ=90-θ
より△QPBも二等辺三角形。
QP=QBであり、まとめると
QA=QP=QB
点Pは点Qを中心とする直径ABの円周上にある。
逆に点PがABを直径とする円周上にあるなら
円周角の定理より∠APB=90° \(\square\)
円の弧と中心角の関係、と円周角の定理より
円の内部と外部の点
3点A、Q、Bは円の周上にあるとする。
点Pが直線ABに関してQと同じ側にある時
- 点Pは円の内部にある⇒∠APB>∠AQB
- 点Pは円の周上にある⇒∠APB=∠AQB
- 点Pは円の外部にある⇒∠APB<∠AQB
また逆も成り立つ。
証明
点Pは円の内部
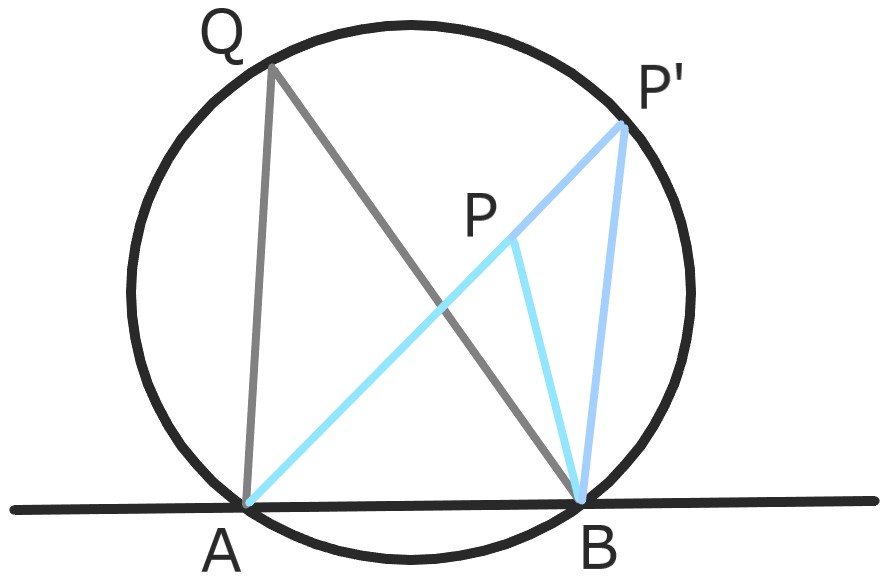
直線APと円の交点をP'とおく。
円周角の定理より∠AQB=∠AP'B
∠APBは△P'BPの外角なので、
∠APB=∠AP'B+∠P'BP
∠APBは∠P'BPだけ∠AP'Bより大きい。
よって∠APB>∠AP'B=∠AQB
点Pは円の周上
円周角の定理より明らか。
点Pは円の外部
こちらの記事で解説します。
逆側の証明
反対方向の証明は背理法より明らか。
すなわち∠APB>∠AQBであって、
点Pが円の内部に無いとする。
この時Pは円周上または円の外部にあるので
∠APB=∠AQBまたは∠APB<∠AQB
これは∠APB>∠AQBに矛盾する。
残りの二つの証明も同様。\(\square\)
が示された。
円に内接する図形
多角形のすべての頂点が一つの円周上にある時、
この多角形は円に
”内接する”という。
また、その円を多角形の
”外接円”という。
円に内接する四角形
特に四角形の場合、
内角αと向かい合う内角βを
内角αの
”対角”といい
次が成り立つ。
証明
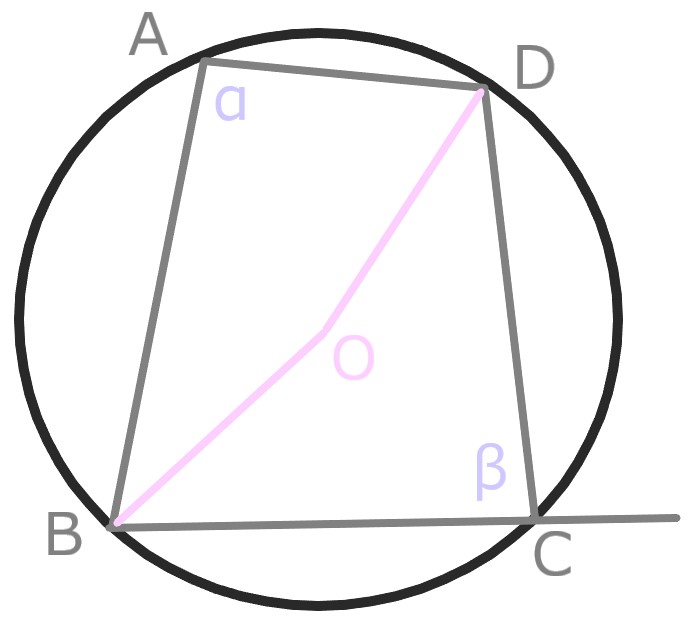
内角αとβは向かい合っているとする。
円周角の定理より、
弧BCDに対する中心角は2α
弧BADに対する中心角は2β
一周は360°なので2α+2β=360
対角の和はα+β=180
またα=180-βでもある。
180-βは∠BCDの外角に等しい。\(\square\)
また逆も成り立つ。
証明

外角が隣り合う内角の対角に等しいなら
対角の和は180°、
四角形ABCDにおいて
∠ABC+∠ADC=180とする。
△ABCの外接円を書き
線分ACについて
点Dと同じ側にある周上に点Eをとる。
四角形ABCEは円に内接するので
∠ABC+∠AEC=180
先の式と見比べて
∠ADC=∠AEC
円周角の定理の逆より点Dも外接円上にある。\(\square\)
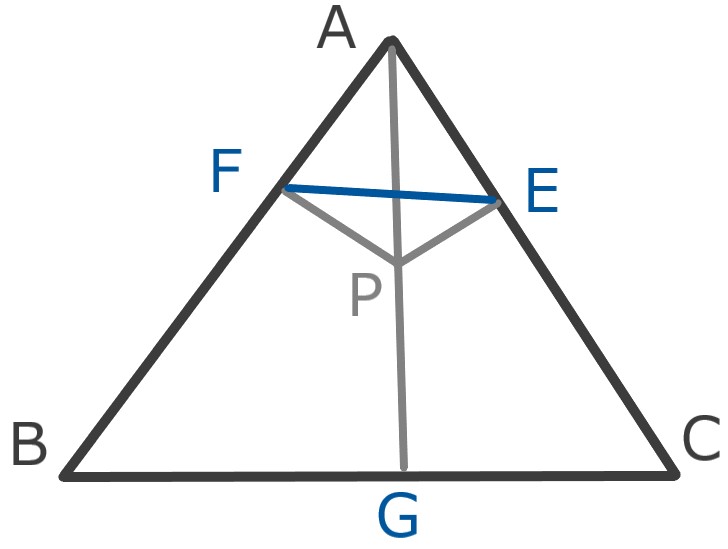
証明
∠AFP+∠AEP=90+90=180なので、
四角形AFPEは円に内接する。
円周角の定理より∠FAP=∠FEP
直角三角形BAGに注目すると
180=∠ABG+∠FAP+90
=∠ABG+(∠FEP+90)=∠FBG+∠FEC
対角の和が180になったので
四角形BCEFは円に内接する。\(\square\)
トレミーの定理
円に内接する四角形において次の等式が成り立つ。
$$ \mathrm{AB} \cdot \mathrm{CD} + \mathrm{AD} \cdot \mathrm{BC} = \mathrm{AC} \cdot \mathrm{BD} \hspace{20cm}$$
証明
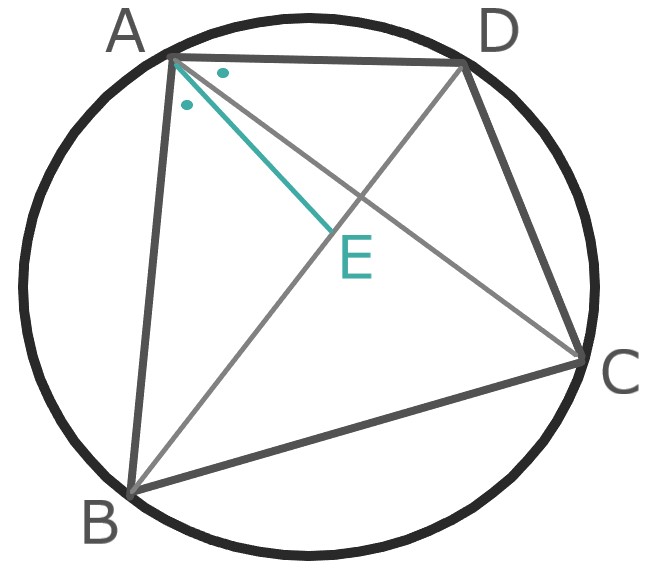
BD上に∠BAE=∠DACとなる様に点Eをとる。
円周角の定理より∠ABE=∠ACDなので、
△ABEと△ACDは相似
$$ \mathrm{AB} : \mathrm{AC} = \mathrm{BE} : \mathrm{CD} \hspace{20cm} $$
よって
$$ \mathrm{AC} \cdot \mathrm{BE} = \mathrm{AB} \cdot \mathrm{CD} \hspace{20cm}$$
また△ABCと△AEDも相似になっている、
$$ \mathrm{AC} : \mathrm{AD} = \mathrm{BC} : \mathrm{ED} \hspace{20cm}$$
から
$$ \mathrm{AD} \cdot \mathrm{BC} = \mathrm{AC} \cdot \mathrm{ED} \hspace{20cm}$$
が言える。
上の二つの式を用いて
$$ \mathrm{AB} \cdot \mathrm{CD} + \mathrm{AD} \cdot \mathrm{BC} = \mathrm{AC} \cdot \mathrm{BE} +\mathrm{AC} \cdot \mathrm{ED} = \mathrm{AC} \cdot \mathrm{BD} \quad \square \hspace{20cm}$$
シムソンの定理
△ABCの外接円上の点Pから
直線AB、BC、CAに垂線PD、PE、PFを降ろす。
この時3点D、E、Fは一直線上にある。
証明
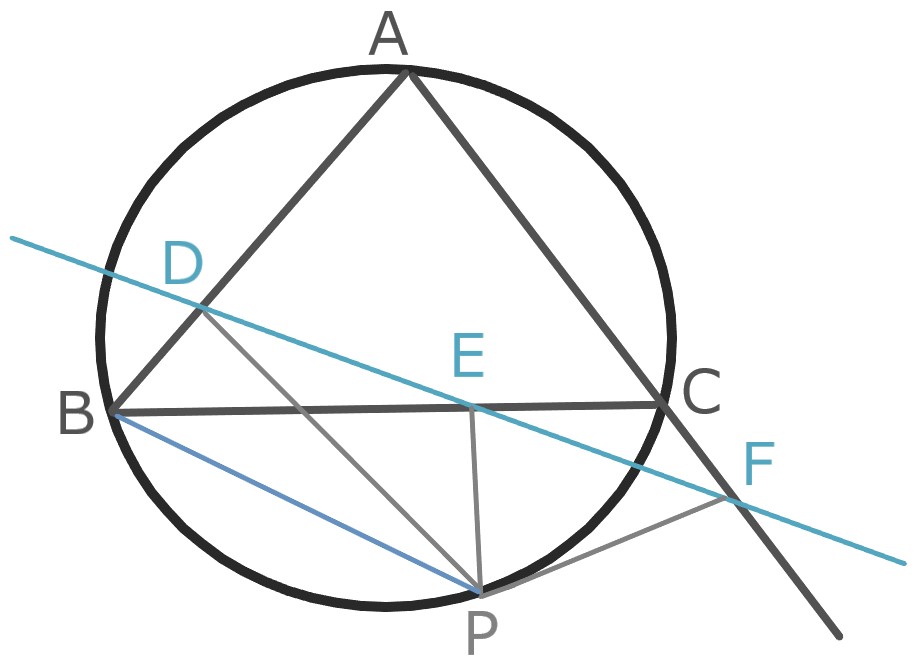
△ABCの内角を∠A、∠B、∠Cと略記する。
∠BDP=∠BEP=90なので、
円周角の定理の逆から
4点B、P、E、Dは一つの円周上にある。
円周角は等しいので∠B=∠DPE
また∠PEC+∠PFC=90+90=180より、
四角形PFCEは円に内接する。
外角は隣り合う内角の対角に等しいので
∠C=∠EPF
∠B+∠C=∠DPE+∠EPF=∠DPF
△PFDに注目すると∠A=∠PDE+∠PFE
円周角は等しいので∠PDE=∠PBE
となり、∠A=∠PBE+∠PFE
補題
ここで∠PBD=∠PEFになっている。
なぜなら、
∠PBD=∠B+∠PBE
∠PEF=180-∠EPF-∠PFE=180-∠C-∠PFE
より
∠PEF-∠PBD=180-∠C-∠B-(∠PFE+∠PBE)=180-∠C-∠B-∠A=0
だからである。
最後に対角の和は180なので
∠PED=180-∠PBD
折れ線DEFは点Eにおいて、
∠PED+∠PEF=180-∠PBD+∠PEF=180
を満たす。
3点D、E、Fは直線上に並んでいる。\(\square\)



