
負の数の累乗(べき乗)は
整数乗までは正の数と同じ計算方法で大丈夫です。
すなわち、
自然数乗は
\( (-1)^n =\underbrace{ (-1) \times (-1) \times \cdots \times (-1) }_{n個} \)
の様に自然数n個分を掛け合わせれば良く
0乗は
\( (-1)^0 = 1 \)
定義より常に1、
マイナス乗は
$$ (-1)^{-n} = \frac{1}{(-1)^n } \hspace{20cm} $$
分母に持って行ってn乗します。
変わって来るのは分数乗を考えた時で
\( (-1)^{1/2} = i \)
負の数の1/2乗の答えは実数の外にあります。
なので高校数学において
負の数の累乗は整数乗に留まり、
実数の範囲に収められる
正の数の累乗に限定して授業が進みます。
この記事は

そもそも累乗とは何?
から始めて定義の土台の指数法則、
負の数の累乗についての曖昧な部分を
学び直せる事を目標にしています。
累乗とは
そもそも累乗(べき乗)とは、
同じ数aを自然数回
掛け合わせることです。
特にaをn回掛け合わせたもの
$$\underbrace{ a \times a \times \cdots \times a}_{n個} \hspace{20cm}$$
をanと書き、aのn乗と呼び
nをその指数と言います。
aを自然数回掛けることは
aが0でも負の数でも可能なので
この時点では、
全ての実数aについて累乗は定義されます。
指数法則
累乗は指数法則という3つの等式を満たします。
- \( a^m a^n = a^{m+n} \)
- \( (a^m)^n = a^{mn} \)
- \( (ab)^n = a^n b^n \)
証明
m、nは自然数とする。
1
$$ a^m a^n = \underbrace{ (a \times \cdots \times a) }_{m個} \times \underbrace{ (a \times \cdots \times a) }_{n個} \hspace{20cm}$$
$$\quad \quad\;\; = \underbrace{ a \times \cdots \times a }_{m+n個}\hspace{20cm}$$
$$ \quad \quad\;\;= a^{m+n} \hspace{20cm}$$
2
$$ (a^m)^n = (\underbrace{ a \times \cdots \times a }_{m個})^n \hspace{20cm}$$
$$ \quad \quad\;\;\;= \underbrace { (\underbrace{ a \times \cdots \times a ) }_{m個} \times \cdots \times \underbrace{ (a \times \cdots \times a) }_{m個} }_{n個} \hspace{20cm}$$
$$ \quad \quad\;\;\; = \underbrace{ a \times \cdots \times a }_{mn個} \hspace{20cm}$$
$$ \quad \quad\;\;\; = a^{mn}\hspace{20cm} $$
3
$$ (ab)^n =\underbrace{ ab \times ab \times \cdots \times ab }_{n個} \hspace{20cm}$$
$$\quad \quad\;\; = \underbrace{(a \times \cdots \times a)}_{n個} \times \underbrace{(b \times \cdots \times b)}_{n個} \hspace{20cm}$$
$$\quad \quad\;\;= a^n b^n \hspace{20cm}$$
この指数法則が成り立つように
0乗、マイナス乗、1/n乗、m/n乗(有理数乗)、実数乗、
まで指数のとれる値が拡張されて行きます。
0乗

aを0回掛ける
は本来なら意味を成さない文章です。
この様な時に数学では、
計算法則が保たれる値を定義として採用します。
すなわち指数法則が成立する値でaの0乗を定義します。
一番目の指数法則においてn=0とすれば
$$\quad \, a^m a^0 = a^{m+0} \hspace{20cm}$$
$$\Leftrightarrow a^m a^0 = a^m \hspace{20cm} $$
なので
\( a^0 := 1 \)
と定めます。
この定義は残りの二つの指数法則も満たします。
証明
m、nは0以上の整数とする。
2-1
$$\left\{ \begin{eqnarray} (a^m)^0 &=& 1 \\ a^{m \times 0} &=& a^0 = 1 \end{eqnarray} \right. \hspace{20cm}$$
2-2
$$\left\{ \begin{eqnarray} (a^0)^n &=& 1^n = 1 \\ a^{0 \times n} &=& a^0 = 1 \end{eqnarray} \right. \hspace{20cm}$$
3
$$\left\{ \begin{eqnarray} (ab)^0 &=& 1 \\ a^0 b^0 &=& 1 \times 1 = 1 \end{eqnarray} \right. \hspace{20cm}$$
マイナス乗

aをマイナス回掛ける
も意味を成さない文章です。
同様に指数法則を保つよう値を定めます。
自然数nについて一番目の指数法則は
$$\quad \, a^n a^{-n} = a^{n-n} \hspace{20cm} $$
$$\Leftrightarrow a^n a^{-n} = a^0 \hspace{20cm}$$
$$\Leftrightarrow a^n a^{-n} = 1 \hspace{20cm}$$
なので等式を満たすため
$$ a^{-n} := \frac{1}{a^n} $$
と定義します。
この定義には分数を使うので、
aが0だと分母も0になってしまい都合が悪いです。
この時点でa≠0が仮定に追加されます。
指数法則を3つとも満たします。
負の数の1/n乗
\( x^n = a \)
を満たす数xをaのn乗根と言い
2乗根、3乗根、4乗根、…をまとめて累乗根と呼びます。
nが奇数
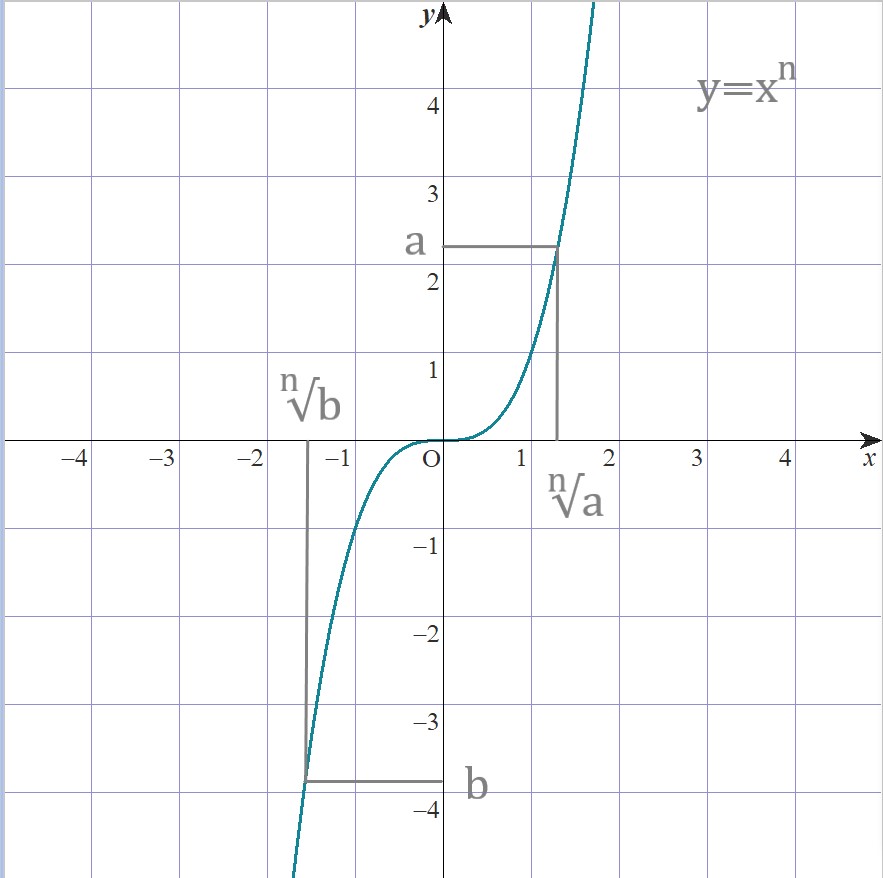
nが奇数の時、関数y=xnは
-∞から+∞まで単調増加するので、
すべての正の数a、負の数bについて
実数のn乗根は唯一つです。
これを
\( \sqrt[n]{a} \quad (= a^{1/n} ) \)
と書きます。
nが偶数
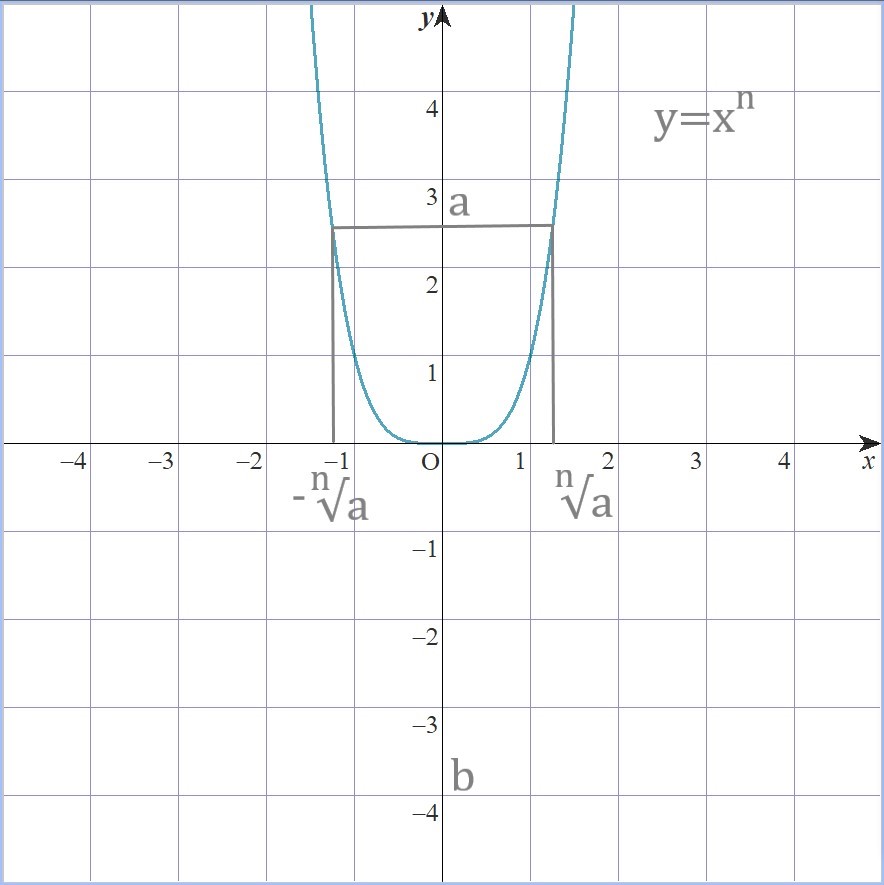
一方、nが偶数の時y=xnは
常に0以上の値をとる偶関数なので
正の数aのn乗根は二つある傍ら、
負の数bのn乗根は実数において存在しません。
\( (-1)^{1/2} = i \)
の様に複素数を許すなら
負の数もn乗根を持ちますが
高校数学では実数までです。
よってa>0が仮定に追加されます。
以降、二つあるaのn乗根の
正の値をaの1/n乗に採用して
次いで有理数乗と実数乗が定義されて指数関数、
\( y = a^x \quad (a>0) \)
が作られます。
まとめ
負の数の累乗は
整数乗まで正の数と区別なく定義され、
計算の仕方、指数法則を満たす事も
正の数の累乗と一緒になります。
負の数のn乗根は複素数になってしまうので
実数の指数関数を作るべく、
底を正の数に限定して進んで行きます。
参考文献
大学数学ですが底が負の場合の記事です。

