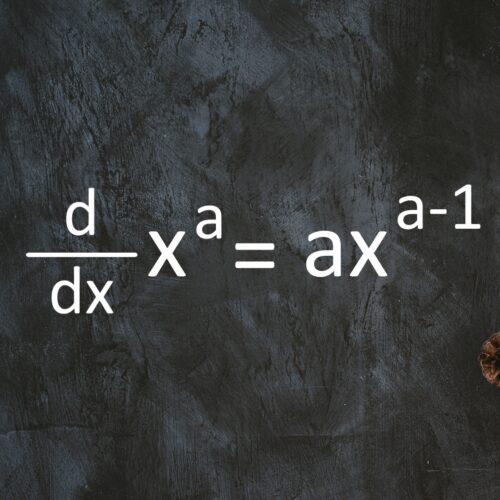べき関数は高校数学において
一次関数、二次関数や
分数関数、無理関数など
色々な名前で登場し
気付いたらべき関数と知らずに
勉強が済んでいる、という代物です。
べき関数の定義と諸性質を
グラフを描きつつ、
わかりやすく説明したいと思います。
べき関数の定義
aを実数として
\( y = x^a \)
の様に書かれる関数をべき関数と呼びます。
漢字だと巾関数、または冪関数です。
aを自然数nに限れば
\( y = x^n \)
お馴染みの一次関数や二次関数になります。
例えばy=xは最も良く知られたべき関数です。
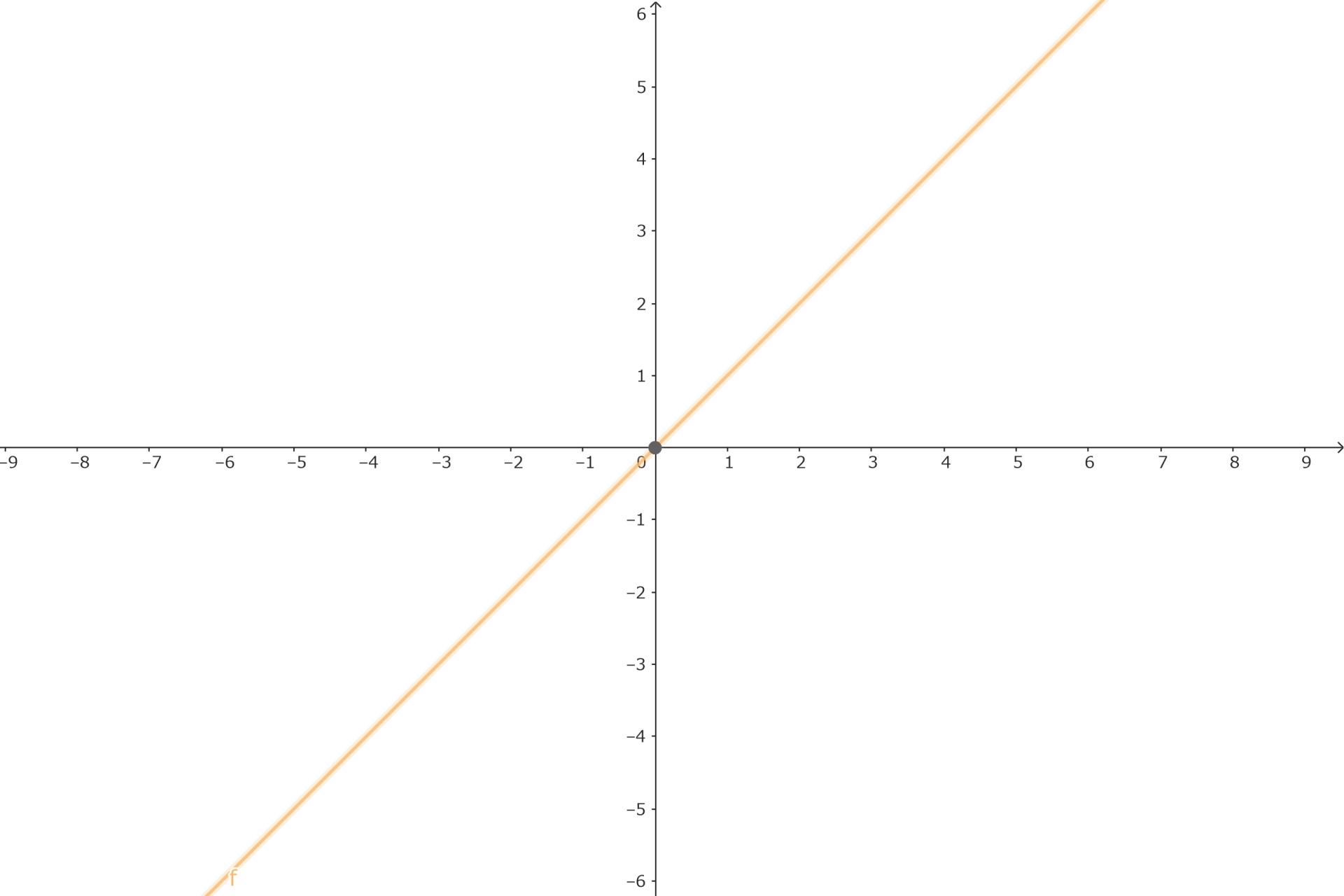
指数関数との違い
べき関数と混同されやすいのが指数関数です。
aを実数として
指数関数
\( y = a^x \)
べき関数
\( y = x^a \)
です。
aとxを入れ換えただけ、なので似ています。
両者には密接な関係があり
学校では、
- 自然数乗のべき関数(y=x2、1~n次関数)
- 指数関数
- 整数乗のべき関数(y=1/x、分数関数)
- 有理数乗のべき関数(y=√x、無理関数)
- 実数乗のべき関数
の順番で勉強します。
n次関数から始まり指数関数に寄り道、
指数の拡張を通じて
累乗の定義を実数まで広げ
再びべき関数に帰って来ます。
べき関数→指数関数→べき関数
なのも頭の中で混ざる原因です。
↓累乗の定義はこちら。

べき関数の性質
定義域と極限
べき関数y=xaの定義域はaの値によって変わります。
自然数乗
aが自然数nの時
\( y = x^n \)
であり定義域は実数全体です。
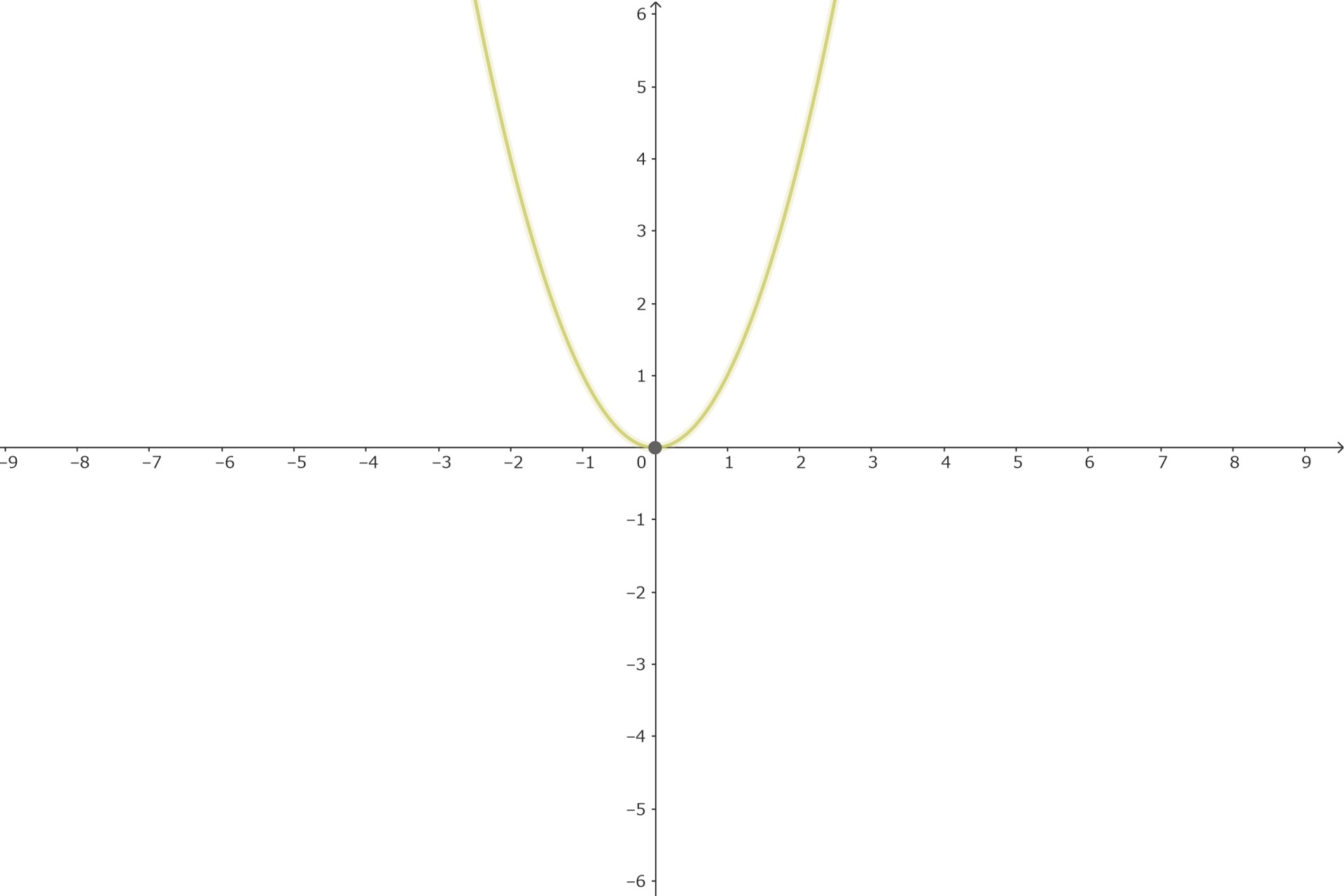
n=偶数
nを偶数とすると
$$\left\{ \begin{eqnarray} \lim_{x \to -\infty} x^n = \infty \\ \lim_{x \to \infty} x^n = \infty \end{eqnarray} \right. \hspace{20cm}$$
を極限に持つ偶関数です。
n=奇数
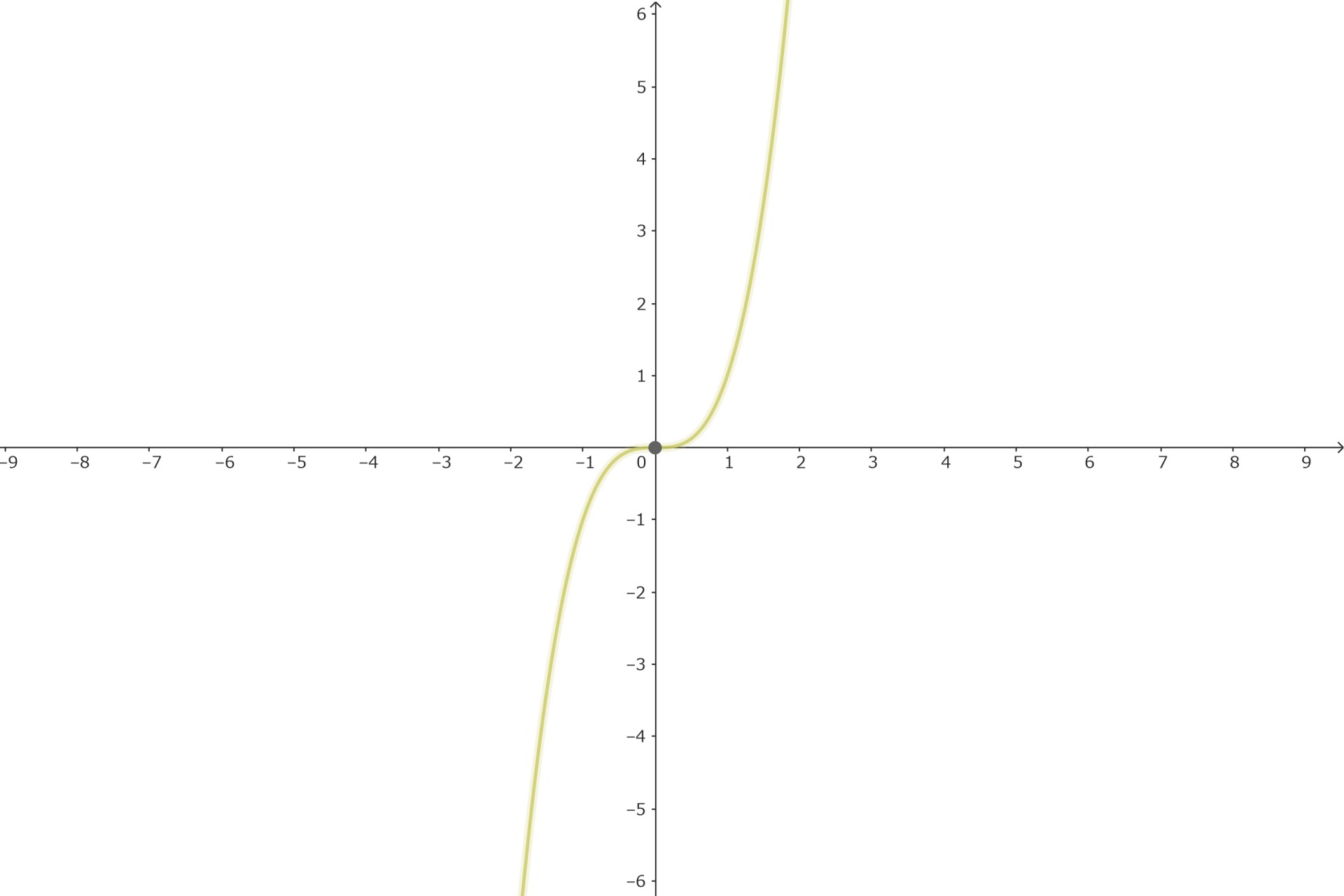
またnを奇数とすると
$$\left\{ \begin{eqnarray} \lim_{x \to -\infty} x^n &=& -\infty \\ \lim_{x \to \infty} x^n &=& \infty \end{eqnarray} \right. \hspace{20cm}$$
を極限に持つ奇関数かつ単調増加です。
a=0
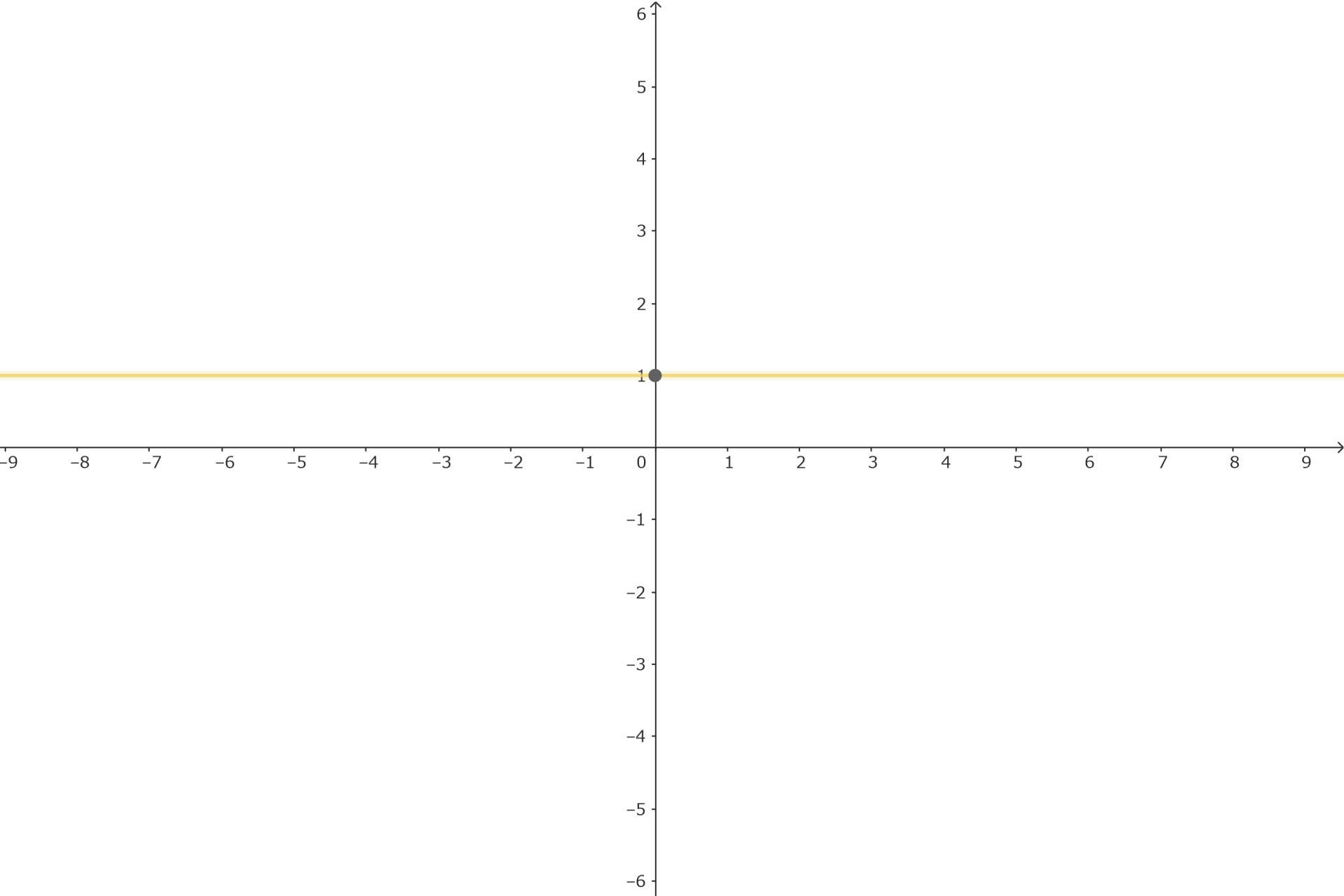
aが0の時は
\( y = x^0 = 1 \)
常に1の定数関数になります。
負の数乗
aが負の数-nの時
$$ y = x^{-n} = \frac{1}{x^n} \hspace{20cm}$$
であり定義域は
\( x \neq 0 \)
です。
分母を0にする点を除きます。
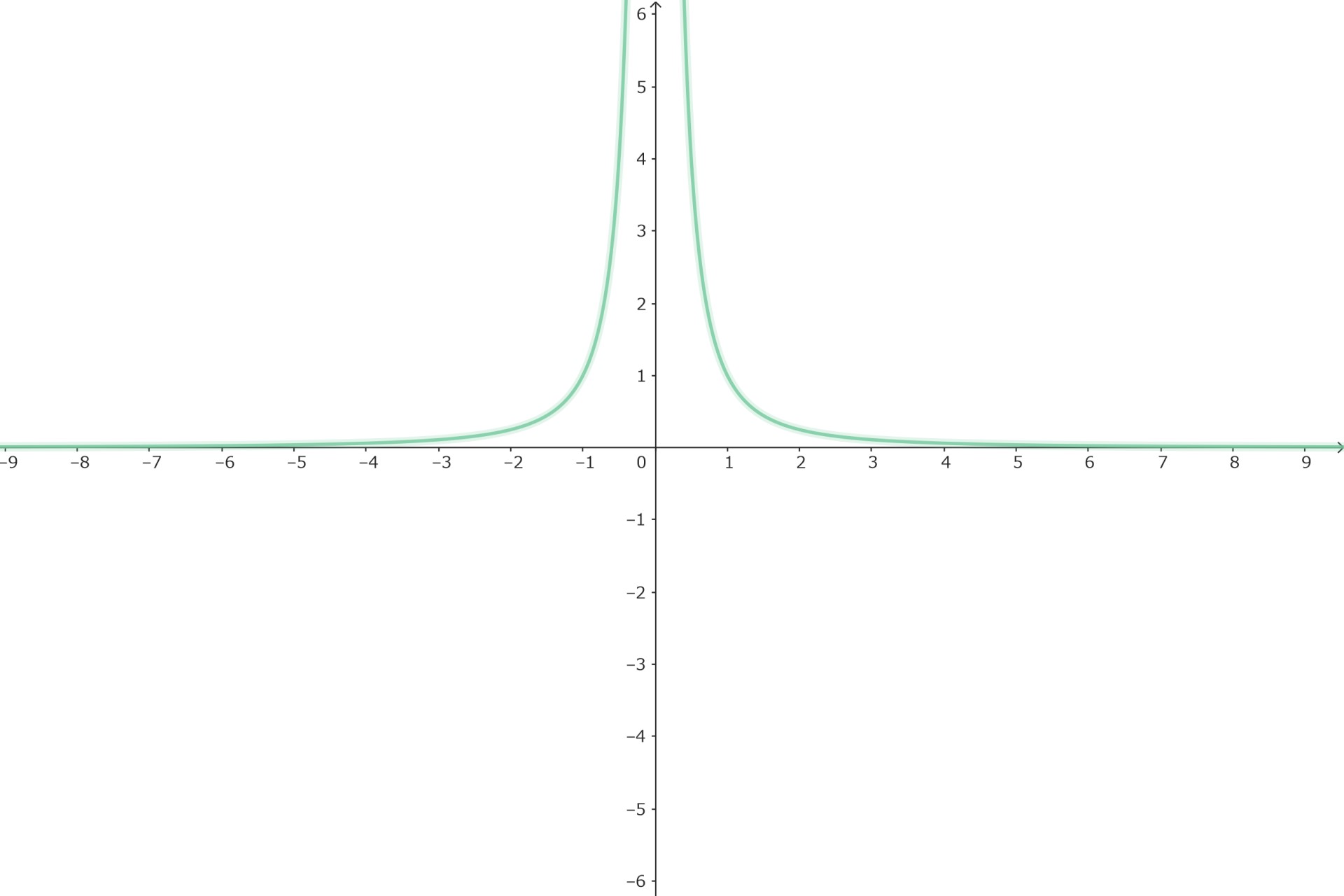
n=偶数
nを偶数とすると
$$\left\{ \begin{eqnarray} \lim_{x \to -\infty} x^{-n} = 0 \\ \lim_{x \to \infty} x^{-n} = 0 \end{eqnarray} \right. \quad \quad \quad \quad \quad \quad\quad$$
$$\left\{ \begin{eqnarray} \lim_{x \to -0} x^{-n} = \infty \\ \lim_{x \to +0} x^{-n} = \infty \end{eqnarray} \right. \hspace{20cm}$$
を極限に持つ偶関数です。
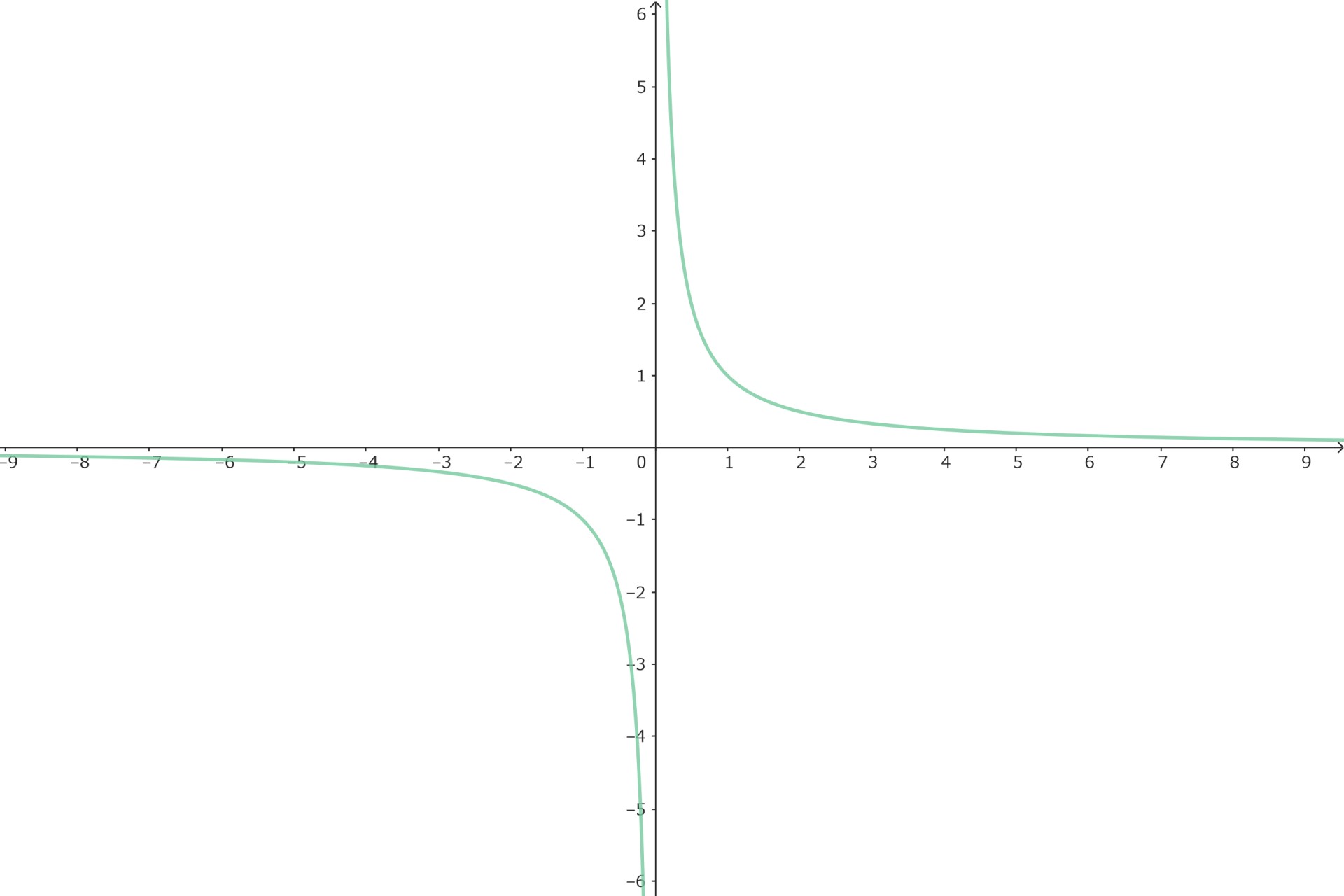
n=奇数
またnを奇数とすると
$$\left\{ \begin{eqnarray} \lim_{x \to -\infty} x^{-n} = 0 \\ \lim_{x \to \infty} x^{-n} = 0 \end{eqnarray} \right. \quad \quad \quad \quad \quad \quad\quad$$
$$\left\{ \begin{eqnarray} \lim_{x \to -0} x^{-n} &=& -\infty \\ \lim_{x \to +0} x^{-n} &=& \infty \end{eqnarray} \right. \hspace{20cm}$$
を極限に持つ奇関数です。
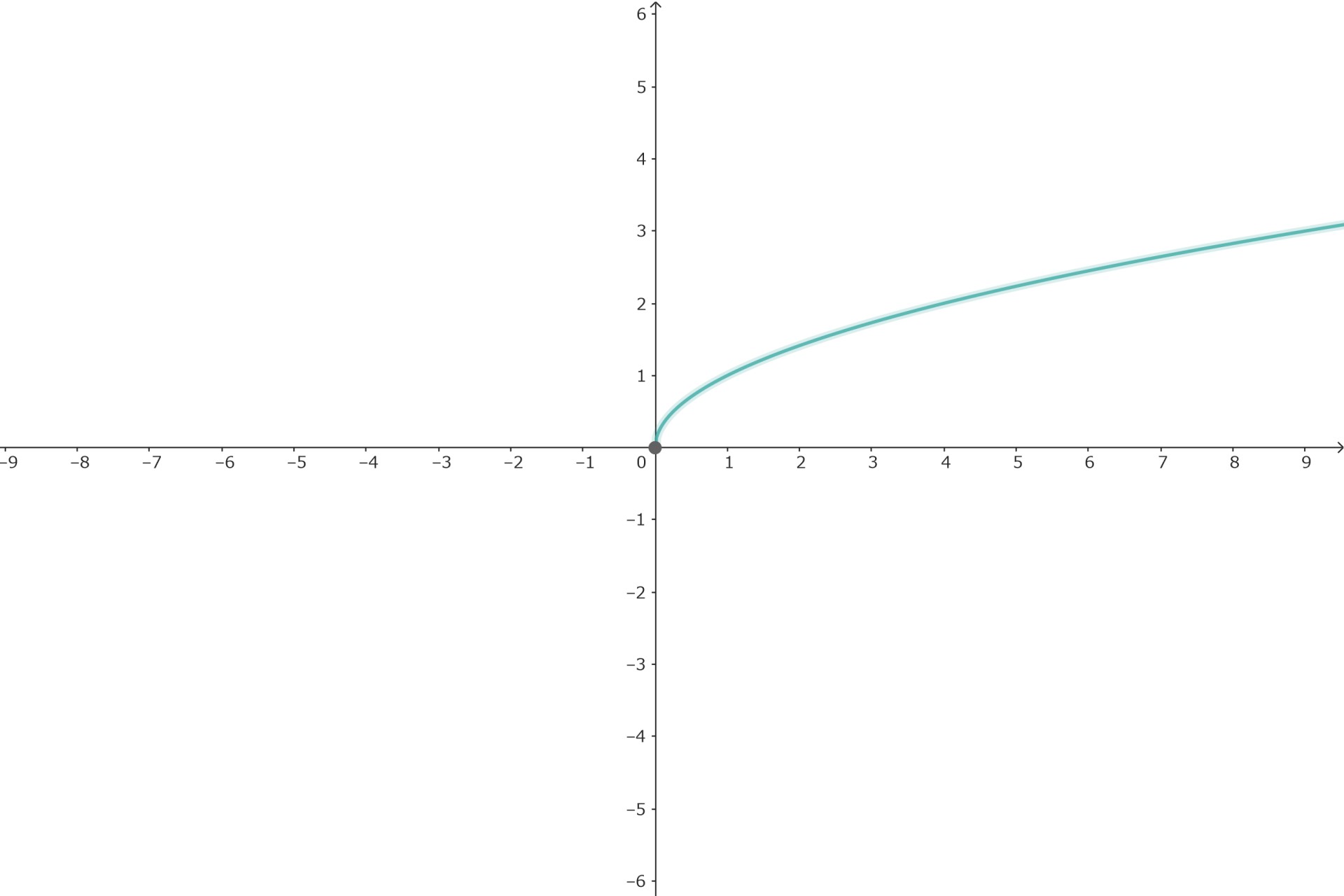
1/n乗
aが自然数nの逆数1/nの時は
\( x \geq 0 \)
を定義域に持ちます。
点0における値は0、極限は
\( \lim_{x \to \infty} x^{1/n} = \infty \)
です。
有理数乗
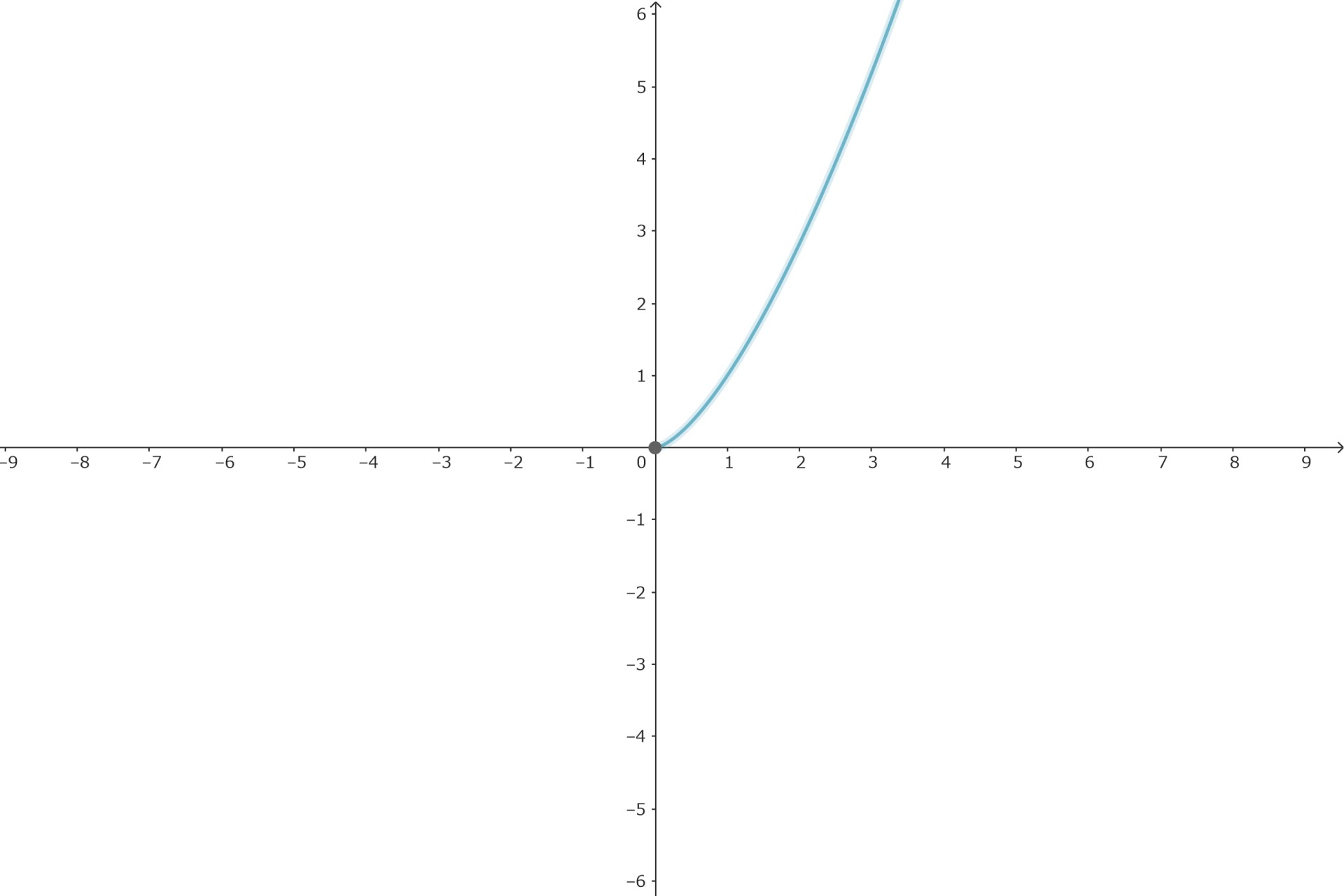
正の有理数乗
aが正の有理数m/nの時は、
指数法則より
\( y = x^{m/n} = (x^{1/n})^m \)
なので、1/n乗のグラフをm乗した物になります。
定義域は等しくx≧0
点0の値は0、極限はプラスの無限大です。
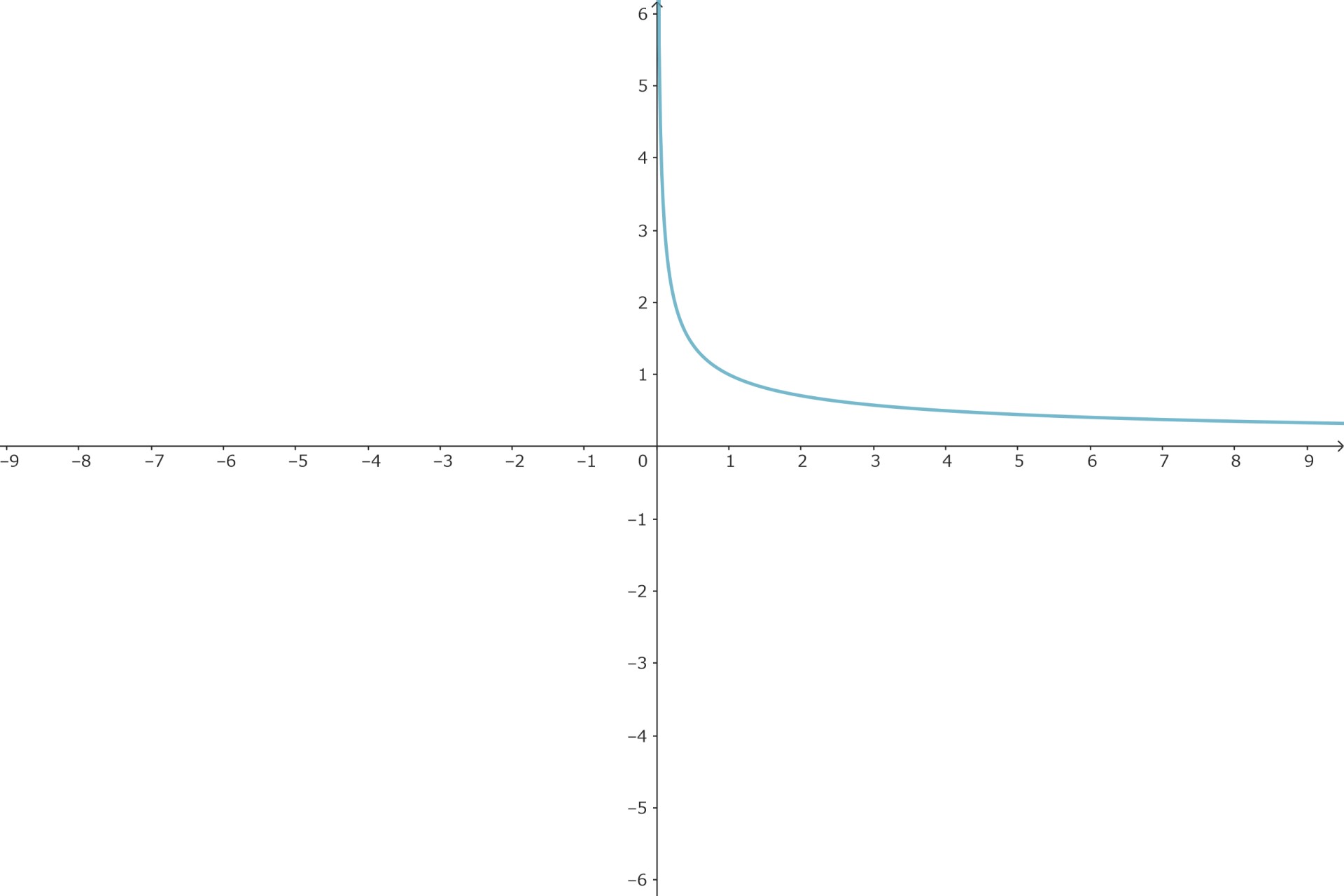
負の有理数乗
aが負の有理数-m/nの時は、
指数法則より
$$y = x^{-m/n} = (x^{m/n})^{-1} = \frac{1}{x^{m/n}} \hspace{20cm} $$
なので正の有理数乗のグラフの逆数をとります。
定義域は
\( x>0 \)
に変わります。
分母0の点を避けます。
$$\left\{ \begin{eqnarray} \lim_{x \to 0} x^{-m/n} &=& \infty \\ \lim_{x \to \infty} x^{-m/n} &=& 0 \end{eqnarray} \right. \hspace{20cm}$$
を極限に持ちます。
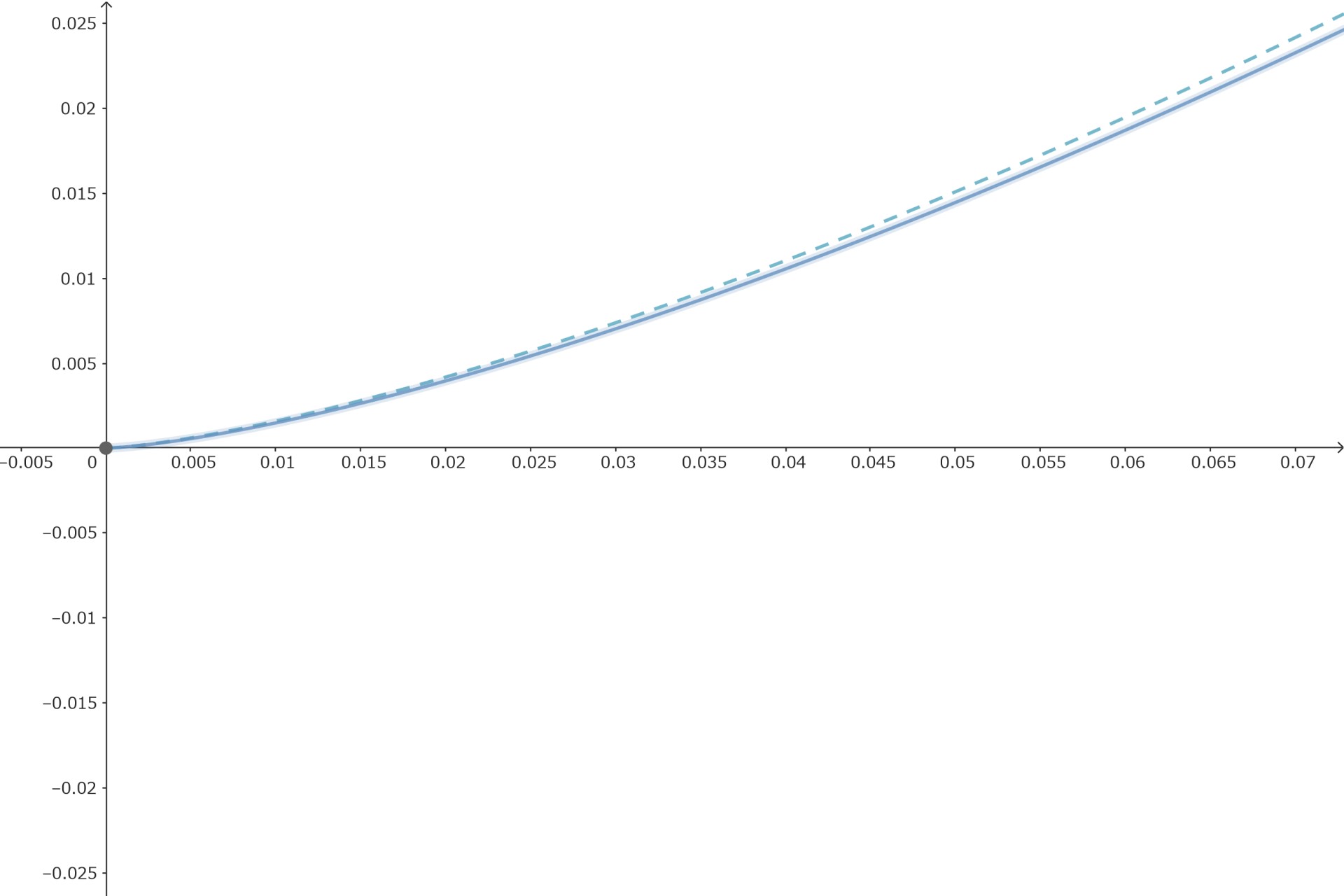
無理数乗
無理数乗のべき関数は
有理数乗の極限として与えられます。
\( y = x^\sqrt{2} = \lim_{n \to \infty} x^{r_n} \)
ここで{rn}は$$ \lim_{n \to \infty} r_n = \sqrt{2} $$を満たす有理数列。
有理数乗のべき関数で近似できるので
グラフの形、極限も同じになります。
逆関数
べき関数は逆関数もべき関数です。
a≠0として
$$\left\{ \begin{eqnarray} f(x) &=& x^a \\ g(x) &=& x^{1/a} \end{eqnarray} \right. \hspace{20cm}$$
と置くと指数法則より
\( f(g(x)) = (x^{1/a})^a = x^{a/a} = x \)
また
\( g(f(x)) = (x^a)^{1/a} = x^{a/a} = x \)
も成り立つので
xaの逆関数はx1/aになります。
この際、定義域が変わる事があり要注意です。
連続性
べき関数は連続で
\( y' = a x^{a-1} \)
を導関数に持ちます。
まとめ
べき関数、と聞くと

何それ?
と思いますが種を明かせば
\( y = x^a \)
の事です。
ここまで見覚えのあるグラフも多かったと思います。
基本的な関数なので
しっかり押さえておきましょう。