【(x^a)'=ax^a-1】
べき関数の微分公式を厳密に証明します

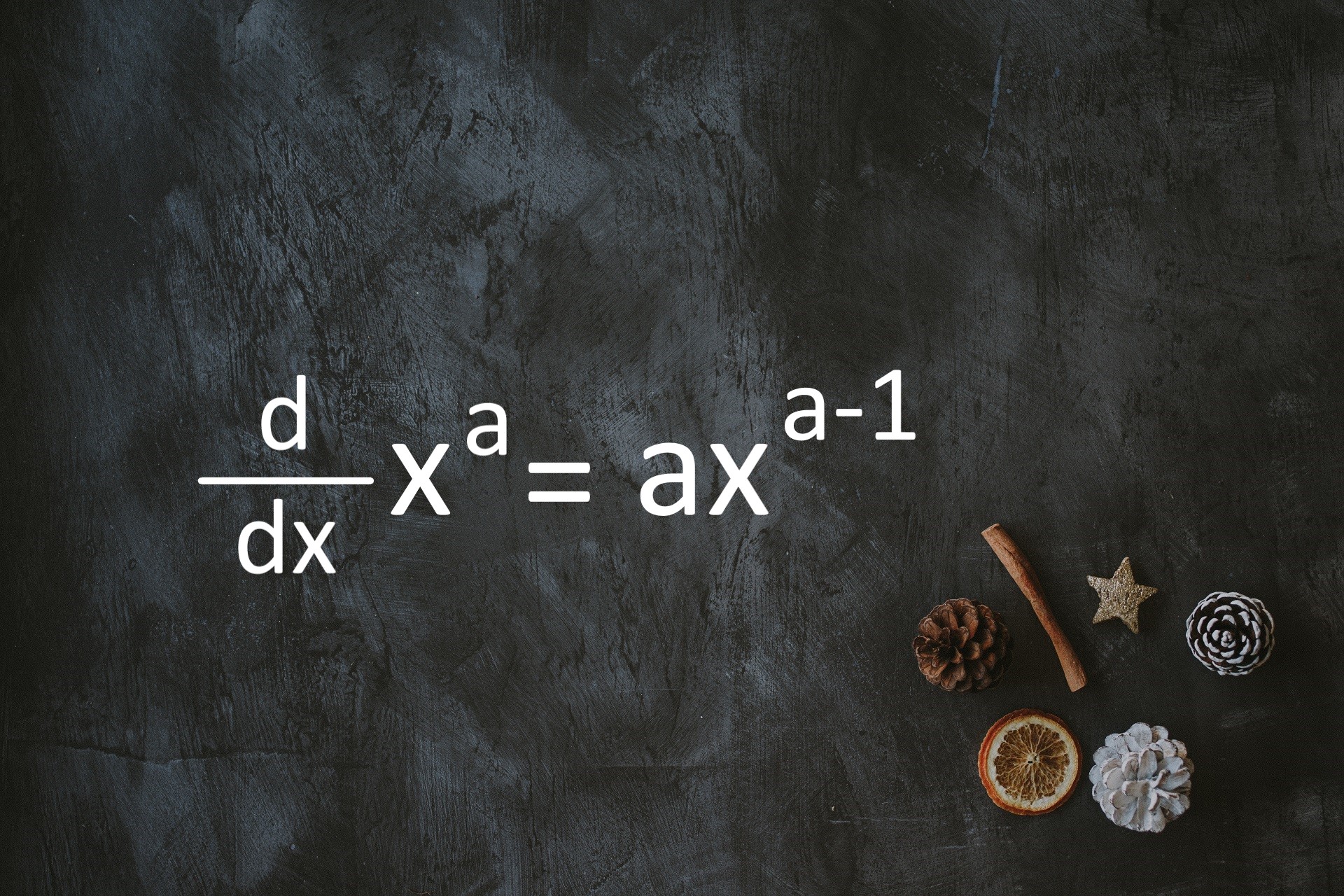
べき関数y=x^aの微分はax^a-1で

微分可能だから連続、
という事を知っている人は多いと思います。

難しいのは証明の道筋で

• 整数乗のべき関数の微分
• 有理数乗のべき関数の連続性
• 実数乗の指数法則
• 指数関数・対数関数の微分
• 実数乗のべき関数の微分

この順番で示さないと
循環論法に陥ってしまいます。

良くある罠としては、

対数微分法を用いて
有理数乗のべき関数の微分は求まりますが

連続性は示されません。

根拠と結論を明白にしつつ

べき関数の連続性と導関数を証明して行きます。

べき関数の連続性と微分

自然数乗のべき関数

自然数nについて
べき関数y=xⁿは実数全体で定義され、

導関数

$(x^n)' = n x^{n-1}$

を持つ。

証明

二項定理より

$(x+h)^n = x^n +n x^{n-1} h + {}_n \mathrm{C}_2 x^{n-2} h^2 +$

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\; \cdots + {}_n \mathrm{C}_{n-2} x^2 h^{n-2} +n x h^{n-1} +h^n$

なので

$$\quad \lim_{h \to 0} \frac{(x+h)^n -x^n }{h} \hspace{20cm}$$

$$= \lim_{h \to 0} \frac{n x^{n-1} h + {}_n \mathrm{C}_2 x^{n-2} h^2 + \cdots + n x h^{n-1} +h^n}{h} \hspace{20cm}$$

$$= \lim_{h \to 0} ( n x^{n-1} + {}_n \mathrm{C}_2 x^{n-2} h + \cdots +n x h^{n-2} +h^{n-1} )\hspace{20cm}$$

$=n x^{n-1} \quad \square$

０乗のべき関数

y=x⁰は常に１の定数関数である。

導関数

$(x^0)' = (1)' = 0$

を持つ。

負の数乗のべき関数

自然数nについて

べき関数

$$x^{-n} = \frac{1}{x^n} \hspace{20cm}$$

はx≠0において定義され、

導関数

$(x^{-n})' = -n x^{-n-1}$

を持つ。

証明

を用いる。

xⁿは微分可能かつ導関数はnx^n-1、

$$\left(\frac{1}{x^n} \right)' = -\frac{(x^n)' }{(x^n)^2 } \hspace{20cm}$$

$$\quad\quad\quad\;\,= -\frac{n x^{n-1}}{x^{2n} } = -n\frac{1}{x^{n+1} } = -n x^{-n-1} \quad \square \hspace{20cm}$$

有理数乗のべき関数連続性

微分可能ならば連続なので
整数乗のべき関数は連続です。

逆関数と合成関数の連続性を利用して、

有理数乗のべき関数の連続性を示します。

狭義単調減少な場合も同様に成り立つ。

x≧0において

y=xⁿは狭義単調増加な連続関数、

逆関数x^1/nもx≧0で連続。

x>0において

y=x^-nは狭義単調減少な連続関数、

逆関数x^-1/nもx>0で連続。

正の有理数乗のべき関数

べき関数x^1/nはx≧0、

x^mは実数全体で連続性を持つ。

合成関数

$y = (x^{1/n})^m = x^{m/n}$

はx≧0において連続。

負の有理数乗のべき関数

べき関数x^-1/nはx>0、

x^mは実数全体で連続性を持つ。

合成関数

$y = (x^{-1/n})^m = x^{-m/n}$

はx>0において連続。

指数法則へ

実数乗のべき関数を微分するには
指数関数、対数関数の力を借りる必要あります。

始めに、

有理数乗のべき関数の連続性を用いて
実数乗の指数法則を示します。

【大学数学】
実数乗の指数法則の証明（解析学）

高校数学で習う指数法則は有理数乗までで、 実数乗において成り立っているかは厳密な説明を避けています。 この記事では、実数の無理数乗の定義から始めて 指数法則が実数乗の場合も含め成り立つことを証明します ...

指数関数と対数関数

実数乗の指数法則が使えると

が求まります。

この公式で
指数関数と対数関数の導関数は計算され、

それぞれ

$$\left\{ \begin{eqnarray} (e^x)' &=& e^x \\ ( \log x)' &=& \frac{1}{x} \end{eqnarray} \right. \hspace{20cm}$$

です。

実数乗のべき関数

最後に合成関数の微分を利用して
実数乗のべき関数の微分を求めます。

定理

任意の実数aについて

べき関数y=x^aはx>0において定義され、

導関数

$(x^a)' = a x^{a-1}$

を持つ。

証明

べき関数を

$$x^a = e^{\log x^a } =e^{a \log x} \hspace{20cm}$$

の様にy=a log(x)とz=e^yの合成関数として見る。

x>0を区間Iにとれば公式の仮定を満たす。

$$(x^a)'= e^{a \log x} (a \log x )' \hspace{20cm}$$

$$\quad\quad\;= e^{ \log x^a} a \times \frac{1}{x} = x^a \times a \times \frac{1}{x} = a x^{a-1} \quad \square \hspace{20cm}$$

まとめ

二項定理、商の導関数、逆関数、合成関数
指数に合わせて道具を用意しました。

最後の実数乗の場合は主に、

合成関数の微分の応用にあたる
対数微分法が利用されます。

今回は証明の正しさを確認しやすい様
そのまま、

指数関数と対数関数の
合成関数と見て計算しました。

参考文献

証明に用いた諸定理