三角形の性質
三角形において次が成り立つ。
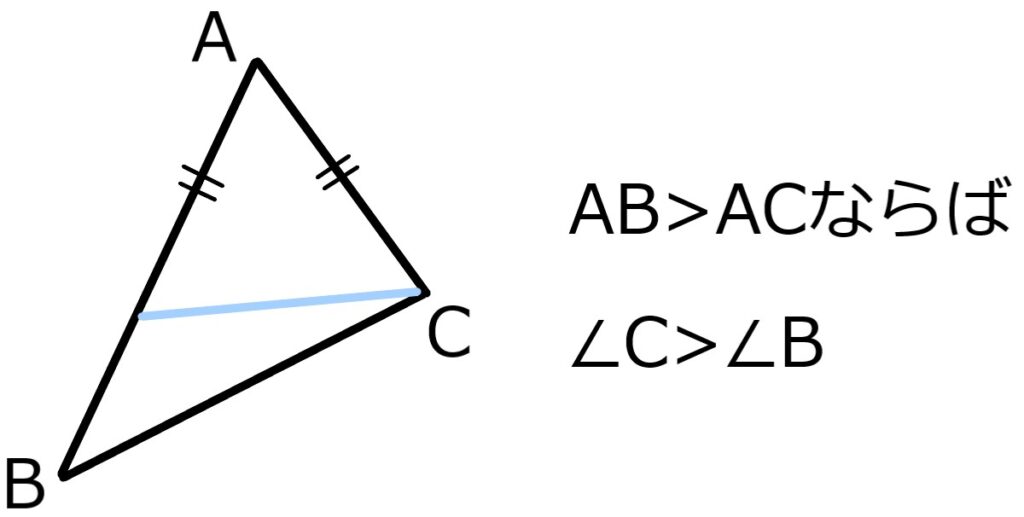
辺と角の大小
定理１
大きい辺に対する角は、小さい辺に対する角より大きい。
角と辺を入れ換えた主張も正しい。
定理２
大きい角に対する辺は、小さい角に対する辺より大きい。
証明
AB>ACとする。
補助線を引き、
ACを一辺に持つ二等辺三角形を作れば自明。
定理２は背理法で示される。
すなわち∠C>∠Bであるのに、
AB≦ACであった時を考える。
AB<ACなら定理１に矛盾し、
AB=ACであれば二等辺三角形より∠C=∠B \(\square\)
２辺の和と差
定理３
２辺の長さの和は、他の１辺の長さより大きい。
また、
定理４
２辺の長さの差は、他の１辺の長さより小さい。
証明
辺BAの延長上に点Dをとり、二等辺三角形ACDを作る。
定理２を使うとBD>BC
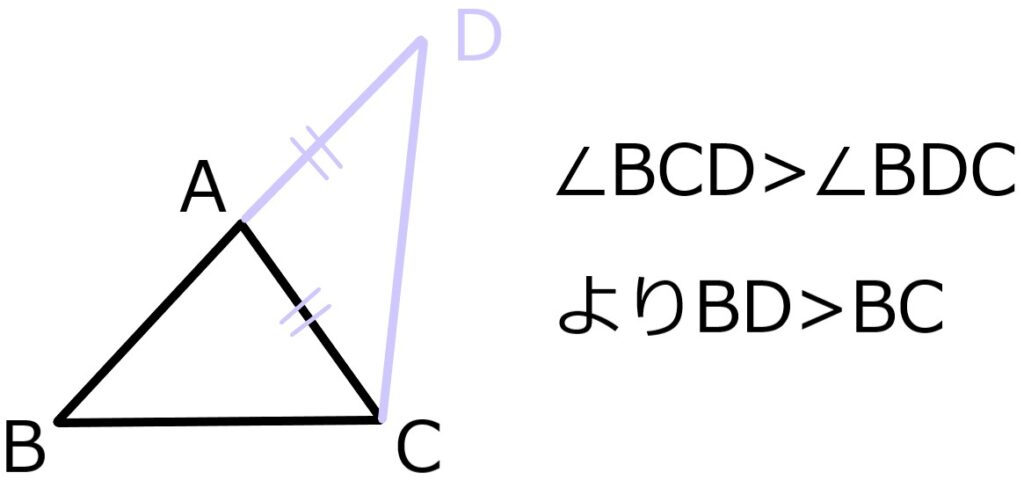
ここでBD=AB+ACなので示された。
定理４は背理法から、
すなわちAB-AC≧BCを仮定し矛盾を導く。
両辺にACを足すと
AB≧BC+ACなので定理３に反する。\(\square\)
Pを三角形ABCの内部の点とすれば
AB+AC>PB+PCである。
証明
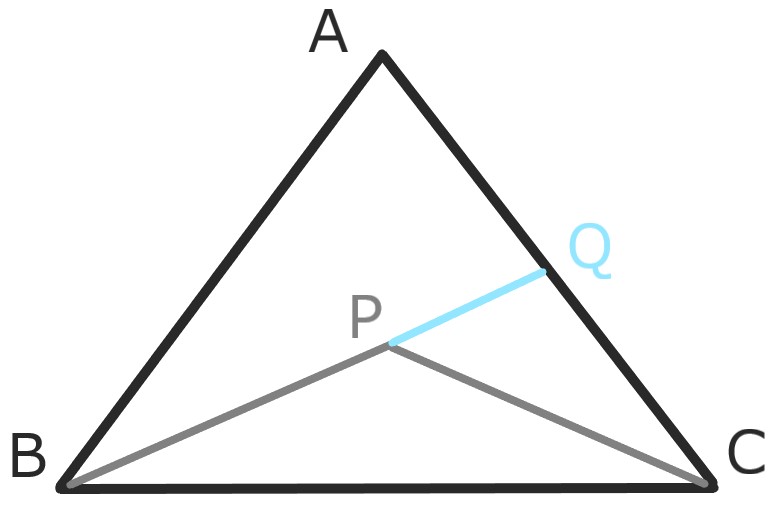
BPの延長と辺ACの交点をQとする。
定理３より
PQ+QC>PC
と
AB+AQ>BQ
を得る。
両辺を足して
AB+(AQ+QC)+PQ>BQ+PC
AB+AC+PQ>(PB+PQ)+PC
両辺からPQを引いて示される。\(\square\)
三角形の存在条件
先の定理より、
三角形の３辺の長さa、b、cは次を満たす。
\( |b-c| < a < b+c \)
逆に正の数a、b、cが上の不等式を満たすなら
これらを３辺の長さに持つ三角形が存在する。
証明
０<θ<180について、
２辺の長さがb、cで
その間の角度がθの三角形は存在する。
三角形の残りの１辺の長さaは、
θに応じて|b-c|からb+cまでの値をとる。\(\square\)
反射の最短距離
直線l上の点PでAP+PBを最小にするものを求めたい。
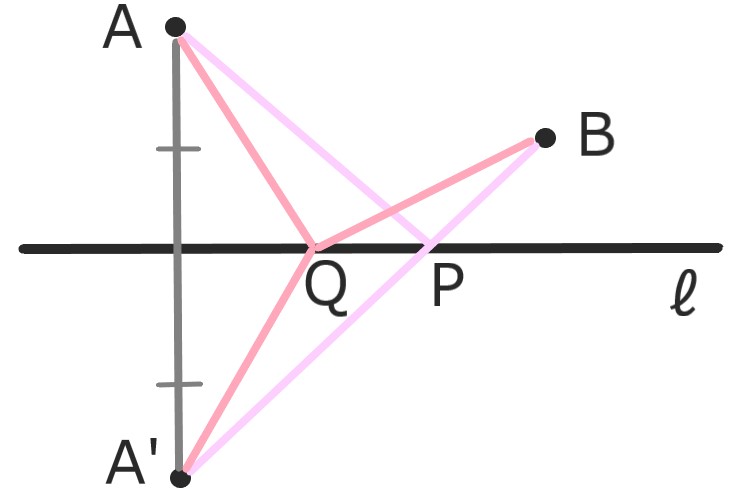
lを軸に点Aと対称の位置に点A’をとる。
A'Bとlの交点が求める点Pである。
証明
l上に点Pでない点Qをとる。
△QA'Bに定理３を適用すればA'Q+QB>A'B
対称性より
A'Q+QB=AQ+QB
A'B=AP+PB
なので示される。\(\square\)
領域内最小の三角形
鋭角XOYの間に点Pがある時、
△PQRの周PQ＋QR＋RPが
最小となる様に点Q、RをOX、OY上にとりたい。
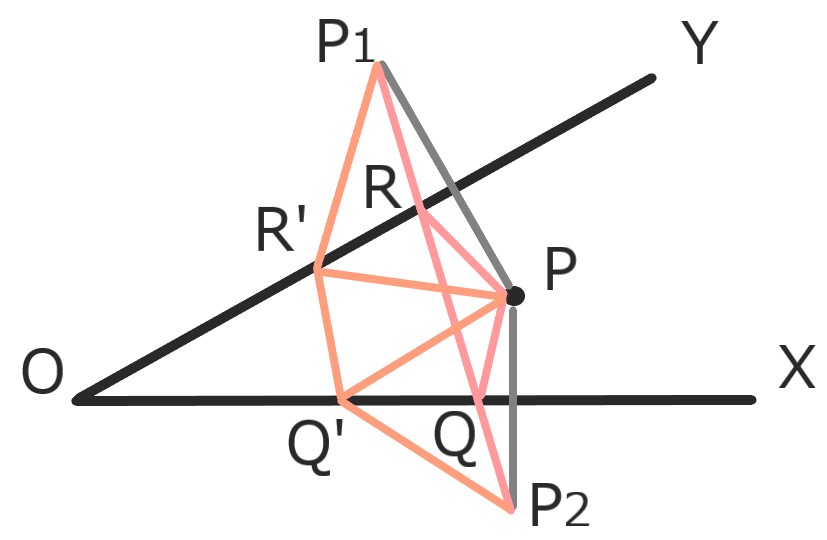
OXとOYについてPと対象の点をP2、P1とし
P2P1とOX、OYとの交点をQ、Rにすれば良い。
証明
点Q'、R'をQ、Rとは異なる点とする。
対称性より
PQ+QR+RP=P2Q+QR+RP1
PQ'+Q'R'+R'P=P2Q'+Q'R'+R'P1
Q'とR'からP2P1に垂線を降ろして考えれば
P2Q+QR+RP1<P2Q'+Q'R'+R'P1 \(\square\)
平行線と線分の比
三角形ABCにおいて
BA、CAの延長上に点B'、C'をとる。
P、Qを半直線AB、AC上または
AB'、AC'上の点とした時、次が成り立つ。
定理５-１
$$ \mathrm{PQ} /\!/ \mathrm{BC} \Leftrightarrow \frac{\mathrm{AP}}{\mathrm{AB}} = \frac{\mathrm{AQ}}{\mathrm{AC}} $$
定理５-２
$$ \mathrm{PQ} /\!/ \mathrm{BC} \Leftrightarrow \frac{\mathrm{AP}}{\mathrm{PB}} = \frac{\mathrm{AQ}}{\mathrm{QC}} $$
定理５-３
$$ \mathrm{PQ} /\!/ \mathrm{BC} \Rightarrow \frac{\mathrm{AP}}{\mathrm{AB}} = \frac{\mathrm{PQ}}{\mathrm{BC}} $$
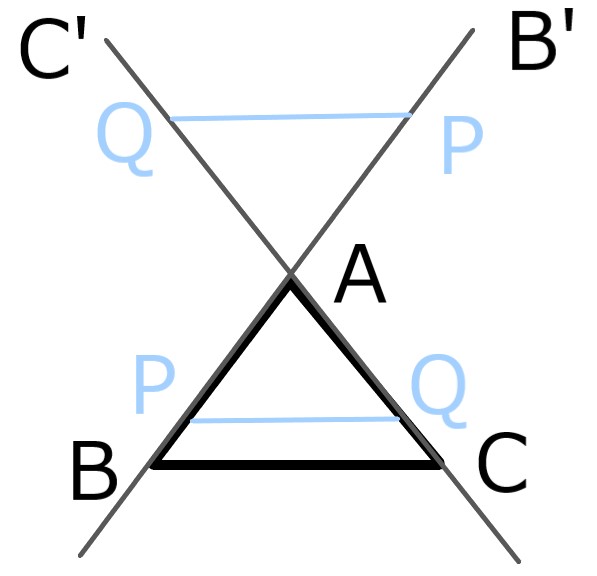
これらは、PQがBCと平行であれば
長さの比が等しくなることを言っている。
ただし定理5-3だけ逆は成り立たない。
反例
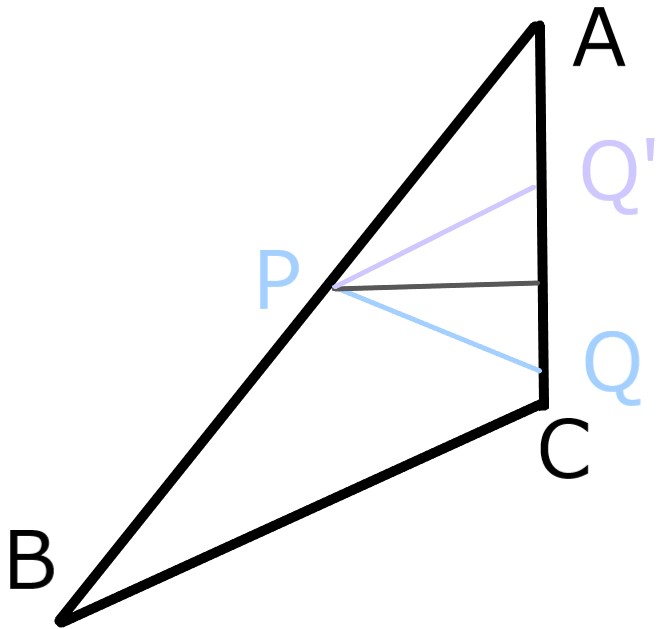
PQ'//BCである様に点P、Q'をとり
PからACに降ろした垂線
について対象の位置に点Qをとる。
この時PQ=PQ'である。
定理5-3よりAP/AB=PQ'/BCなので
AP/AB=PQ/BC
しかしPQ//BCでない。\(\square\)
線分
m、nを正の数とする。
内分点
線分AB上の点Pが
\( \mathrm{AP} : \mathrm{PB} = m : n \)
を満たす時、
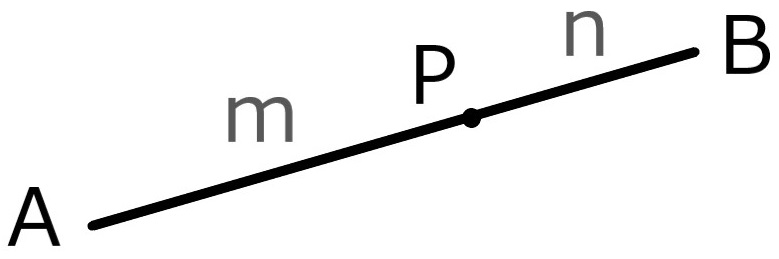
PはABをm:nに
”内分”するといい、
Pを
”内分点”という。
外分点
ABの延長上の点Qが
\( \mathrm{AQ} : \mathrm{QB} = m : n \)
を満たす時、QはABをm:nに
”外分”するといい、
Qを
”外分点”という。
ただしm≠nとする。
外分点の位置は
mとnの大小関係に次の通り従う。
m>nの場合
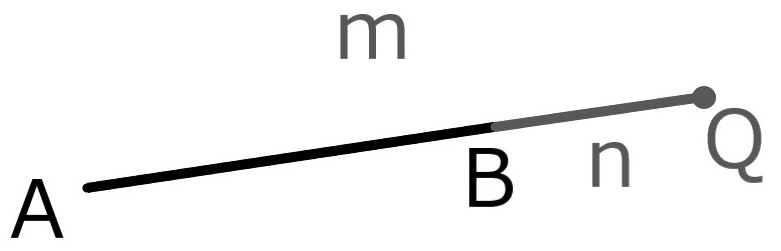
m<nの場合
角の二等分線と比
三角形ABCの角の二等分線について次が成り立つ。
定理６-１
∠Aの二等分線とBCとの交点Pは、BCをAB:ACに内分する。
証明
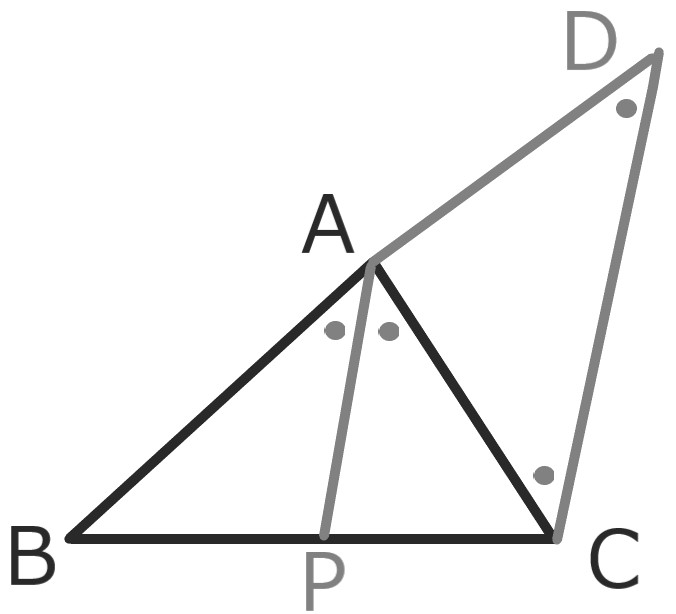
ABの延長上に点DをAP//DCである様とれば、
△ADCは二等辺三角形である。
よってAD=AC
また△BPAと△BCDは相似なので
BP:PC=AB:AD=AB:AC \(\square\)
さらにAB≠ACならば
定理６-２
∠Aの外角の二等分線とBCの延長との交点Qは、
BCをAB:ACに外分する。
証明
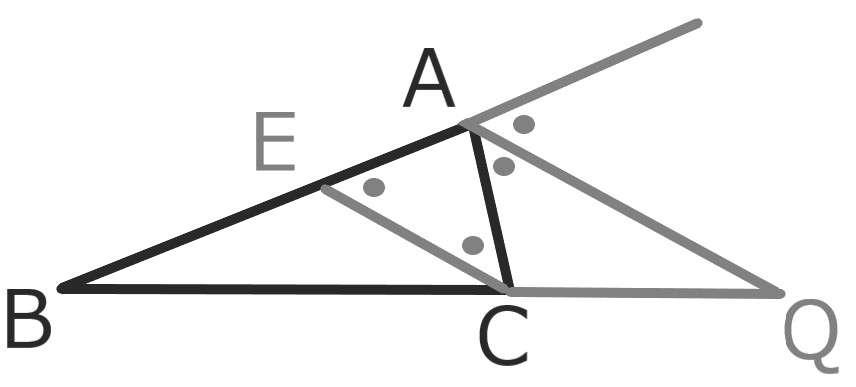
AB上に点EをEC//AQである様とれば、
△AECは二等辺三角形である。
よってAE=AC
EC//AQより△BCEと△BQAは相似なので
BQ:QC=AB:AE=AB:AC \(\square\)
