
三角形の五心
三角形は中心となる点を五つ持つ。
重心
中線
三角形において
頂点と対辺の中点を結ぶ線分を
”中線”という。
この交点を
”重心”という。
証明
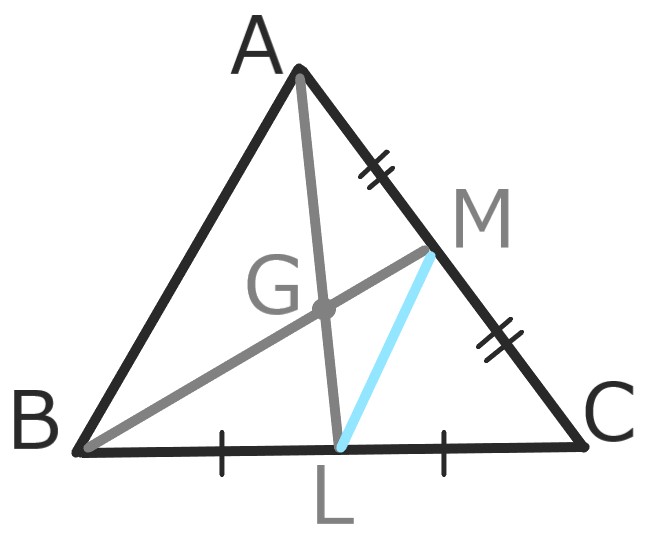
中線ALとBMの交点をGとする。
中点連結定理より
△AGBと△LGMは2:1で相似。
AG:GL=BG:GM=2:1になる。
頂点Cの中線とALの交点をG'とし、
同様に進めれば点GとG'は一致する。\(\square\)
内心
この交点を
”内心”という。
内心を中心とした3つの辺に接する円を
”内接円”という。
証明
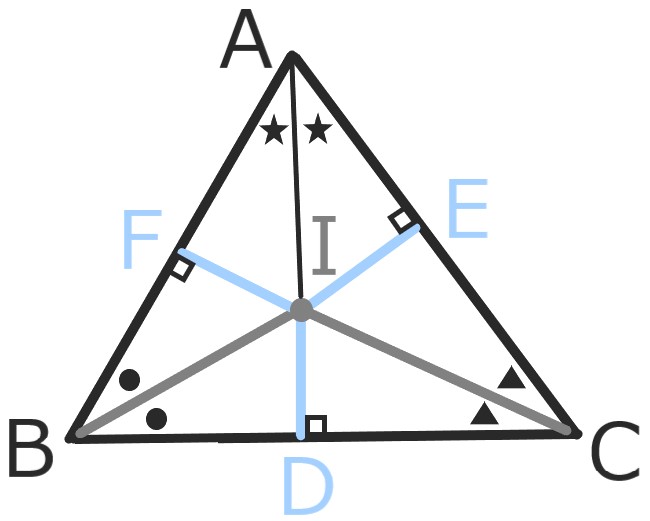
∠Bと∠Cの二等分線の交点をIとし
Iから各辺に垂線を降ろして点D、E、Fをとる。
角度と斜辺が等しいので
△BIF≡△BID、△CID≡△CIE
よってIF=ID=IE
2組の辺の等しい直角三角形なので
△AIE≡△AIF
AIは∠Aの二等分線である。\(\square\)
傍心
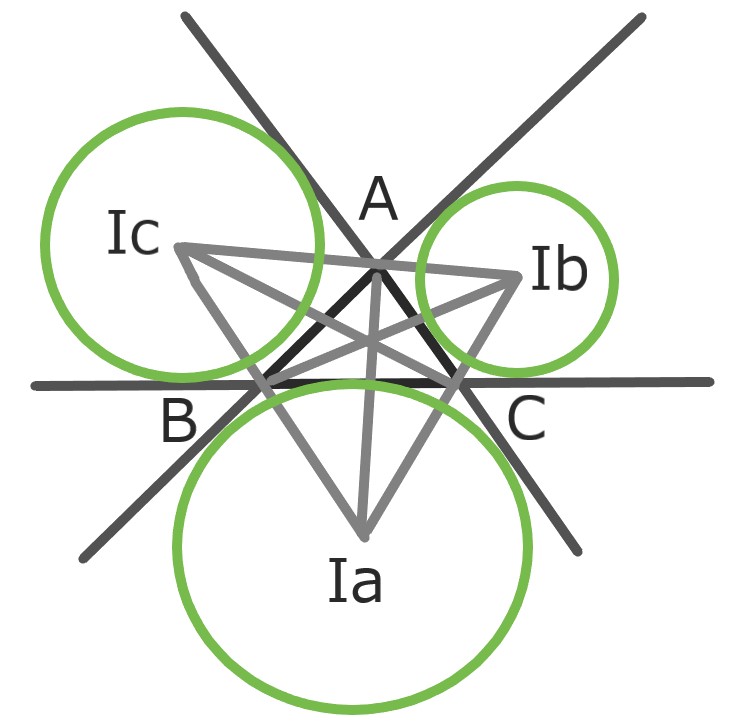
この交点Iaを∠Aの内部における
”傍心”という。
Iaを中心に辺BCと接する様に円を書くと
辺AB、ACの延長とも接する。
この円を
”傍接円”という。
傍心はIa、Ib、Icの全部で3つあります。
△IaIbIcの垂心は△ABCの内心と一致します。
証明
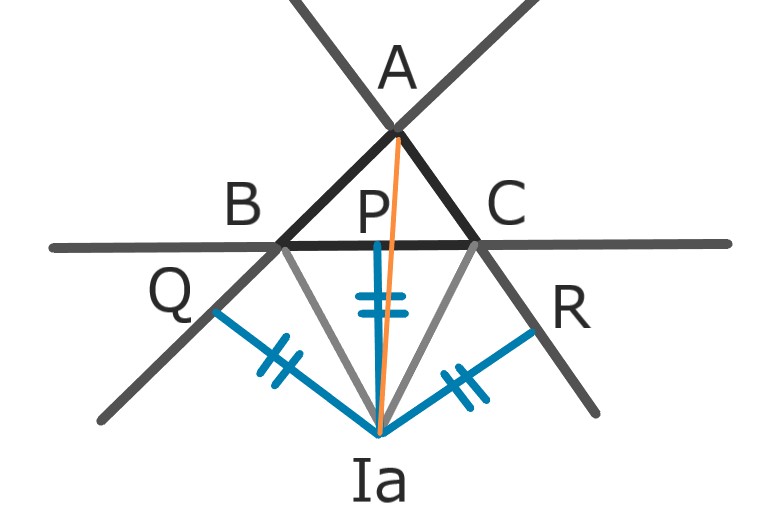
∠Bの外角の二等分線と、
∠Cの外角の二等分線との交点をIaとする。
Iaから辺BCおよび
辺AB、ACの延長上に垂線を降ろして
点P、Q、Rをとる。
角度と斜辺が等しいので
△IaBQ≡△IaBP
△IaCP≡△IaCR
よってIaQ=IaP=IaR
(傍接円を書ける)
また2組の辺の等しい直角三角形なので
△IaAQ≡△IaAR
線分AIaは∠Aの内角の二等分線である。\(\square\)
外心
この交点を
”外心”という。
外心を中心とし、3つの頂点を通る円を
”外接円”という。
証明
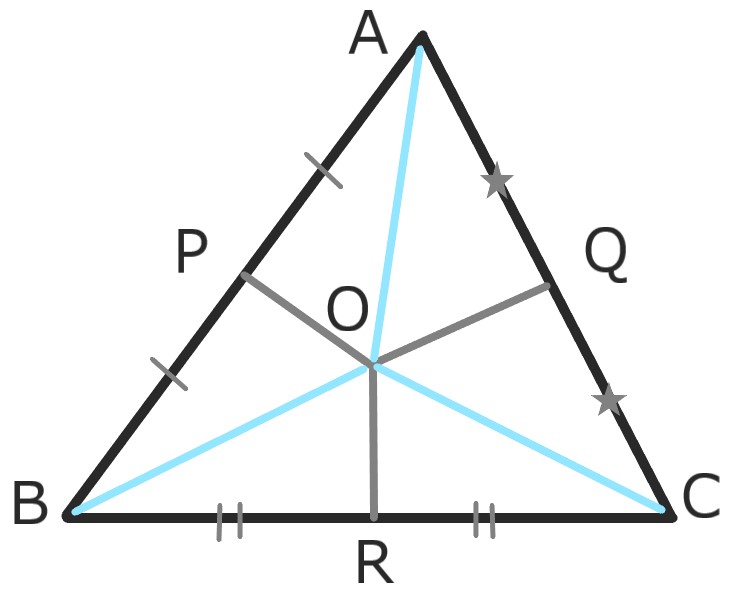
辺ABの垂直二等分線と、
辺ACの垂直二等分線との交点をOとする。
2組の辺の等しい直角三角形なので
△OPA≡△OPB
よってOA=OB
同様にOA=OCであり、
まとめるとOA=OB=OC
点Oから辺BCに垂線をORを引くと
2組の辺の等しい直角三角形なので
△ORB≡△ORC
BR=CRとなり
ORは辺BCの垂直二等分線である。\(\square\)
外心の位置
外心は、
- 鋭角三角形なら内部
- 直角三角形なら斜辺
- 鈍角三角形なら外部
に位置する。
垂心
この交点を
”垂心”という。
証明
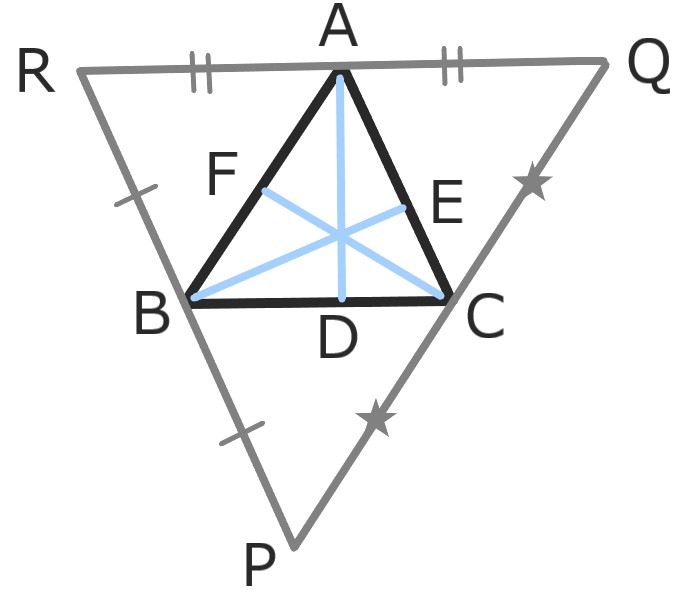
- 点Aを通り辺BCに平行な直線
- 点Bを通り辺CAに平行な直線
- 点Cを通り辺ABに平行な直線
を引いて、三角形PQRを作る。
四角形ABCQとACBRは平行四辺形なので
AQ=BC、RA=BC
RA=AQとなる。
同様に考えてPB=BR、QC=CP
- 垂線ADは辺RQの垂直二等分線
- 垂線BEは辺PRの垂直二等分線
- 垂線CFは辺QPの垂直二等分線
である。
△PQRに外心の定理を用いれば、これらは1点で交わる。\(\square\)
△ABCの垂心は△PQRの外心です。
五心
重心、内心、傍心、外心、垂心を合わせて三角形の
”五心”という。
五心に関する定理
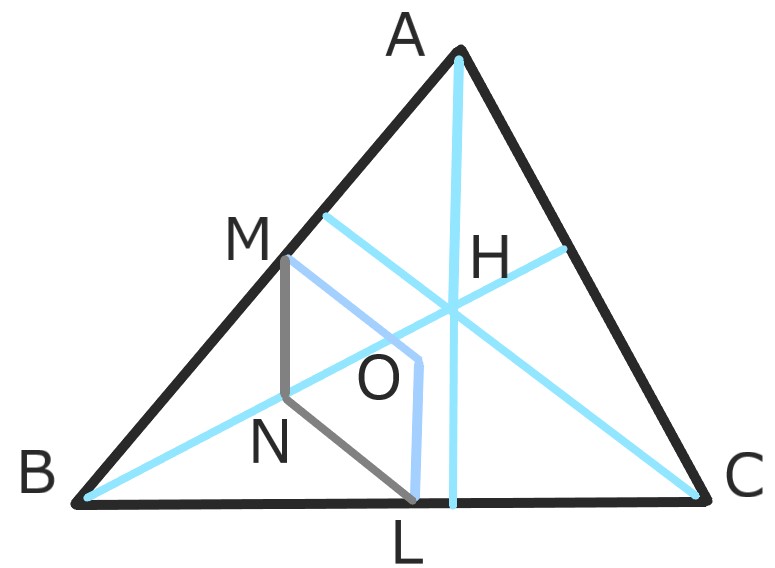
証明
Oから辺ABへの垂線をOM、BHの中点をNとする。
Oは外心なのでMもABの中点よって
中点連結定理よりMN//AH
△BMNと△BAHは1:2で相似である。
同じ辺への垂線なのでAH//OL
MN//OLとなる。
同様に考えてLN//OM
四角形OMNLは平行四辺形になる。
平行四辺形の対辺は等しいので
OL=MN
先程の相似比より2MN=AH
結局、AH=2OL \(\square\)
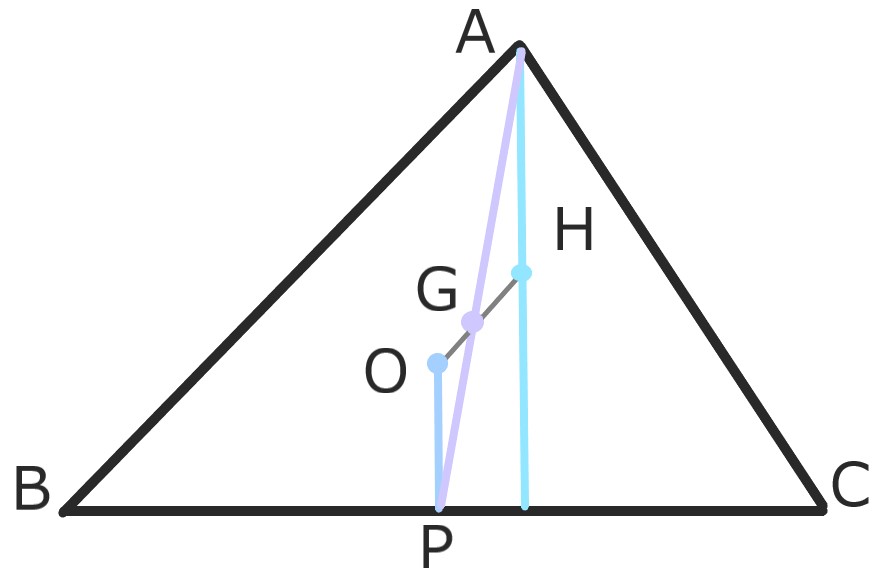
証明
外心O、垂心Hをとり
Oから辺BCに垂線OPを降ろす。
Pは辺BCの中点なので重心はAP上にある。
今、APとOHの交点をGとすれば
AH//OPより
△GOPと△GHAは相似。
また定理1より、その相似比は1:2
重心は中線APを2:1に内分する位置にあるので
Gが重心である。\(\square\)
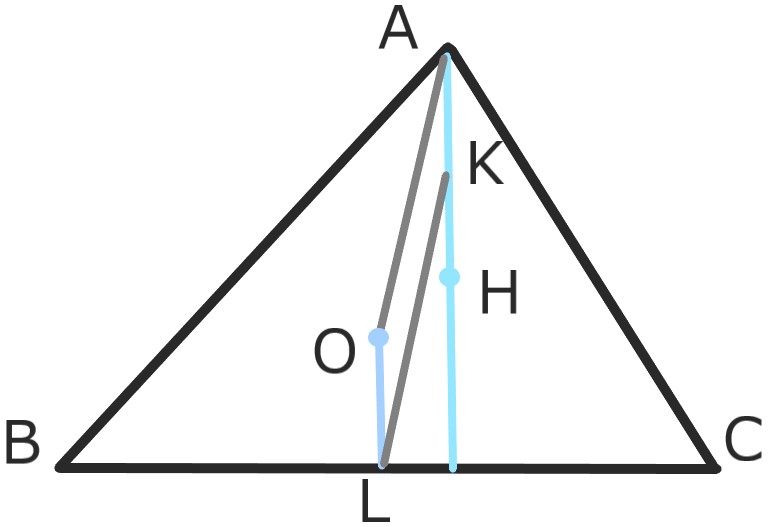
証明
点Oを外心とすればOLは辺BCの垂直二等分線。
定理1よりAH=2OL
またKは中点なのでAH=2AK
よってAK=OLとなり
四角形AOLKは平行四辺形である。
AO=KLともなり
KLは外接円の半径と等しい長さ。\(\square\)
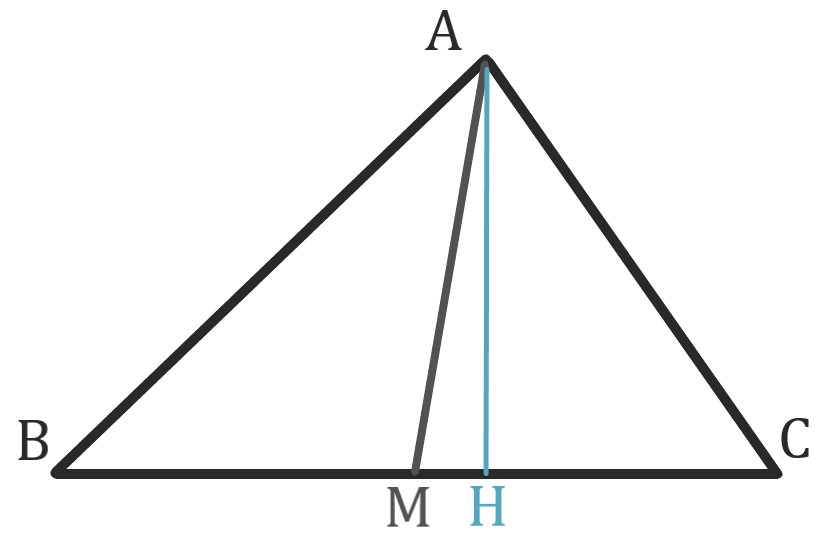
証明
頂点Aから辺BCに垂線AHを降ろす。
この時
\( \mathrm{BH}^2 +\mathrm{CH}^2 = (\mathrm{BM} +\mathrm{MH})^2 +(\mathrm{CM}-\mathrm{MH})^2 \)
右辺はBM=CMなので
\(= (\mathrm{BM} +\mathrm{MH})^2 +(\mathrm{BM}-\mathrm{MH})^2 \)
\(=2(\mathrm{BM}^2 +\mathrm{MH}^2 ) \)
である。
上の関係式より定理は、
\(\quad \mathrm{AB}^2 +\mathrm{AC}^2 \)
\( = ( \mathrm{BH}^2 +\mathrm{AH}^2 ) +(\mathrm{CH}^2 +\mathrm{AH}^2)\)
\(=2(\mathrm{BM}^2 +\mathrm{MH}^2) +2\mathrm{AH}^2 \)
\( =2(\mathrm{BM}^2 +\mathrm{MH}^2) +2(\mathrm{AM}^2 -\mathrm{MH}^2 ) \)
\( =2(\mathrm{AM}^2 +\mathrm{BM}^2 ) \)
と示される。\(\square\)



