高校数学の単語帳１巻

【数学A、C】「確率」
（基礎から条件つき確率まで）の単語帳

事象と確率

試行

同じ状態のもとで繰り返し行うことができて、

その結果が偶然に支配される実験や観察などを

”試行”という。

事象

試行の結果として起こる事柄を

”事象”という。

アルファベットを用い
事象A、事象Bの様に書く。

標本空間

ある試行において
起こり得る場合全体の集合を

その試行の”標本空間”という。

事象は標本空間の部分集合で表される。

事象と、それに対応する部分集合は同一視される。

確率

一つの試行において、

ある事象Aの起きることが期待される割合を

”事象Aの起きる確率”といい

\( P(A) \)

と書く。

同様に確からしい

何個かの事象のどれが起きることも
同じ程度に期待できる時、

これらの事象は

”同様に確からしい”という。

根元事象

標本空間の一つの要素だけからなる集合で表され、

更に細かく分解して考える事のできない事象を

”根元事象”という。

事象Aの起きる確率

各根元事象が同様に確からしい試行ならば

$$ P(A) = \frac{ \verb|事象|A\verb|の起きる場合の数|}{\verb|起き得るすべての場合の数|} \hspace{20cm}$$

であると考える。

より正確には、

標本空間Uにおいて
事象Aを表す部分集合をAとした時

$$ P(A) = \frac{n(A)}{n(U)} \hspace{20cm} $$

とする。

全事象・空事象

標本空間U全体で表される事象を

”全事象”といい

空集合Φで表される事象を

”空事象”という。

積事象・和事象

二つの事象A、Bについて、

AとBが共に起きる事象を

AとBの”積事象”といい

標本空間の部分集合A∩Bで表される。

AまたはBの起きる事象を

AとBの”和事象”といい

標本空間の部分集合A∪Bで表される。

排反

事象A、Bが決して同時に起きない時

AとBは互いに”排反”である

または

互いに”排反事象”である、という。

確率の加法定理

互いに排反な事象A、Bについて次の等式が成り立つ。

定理

\( P(A \cup B) = P(A) +P(B) \)

和事象の確率

また排反であるかに依らず、次の等式が成り立つ。

公式

\( P(A \cup B) = P(A) +P(B) -P(A \cap B) \)

余事象

事象Aに対して「Aが起きない」という事象を

Aの”余事象”という。

これは標本空間ではAの補集合に相当する。

試行と期待値

独立

二つの試行T1、T2において

一方の結果が他方の結果に影響を与えない時

試行T1、T2は”独立”である、という。

複数の試行の組T=(T1、T2、T3、…)で

どの二つの試行も独立であるならば

Tを”独立試行”という。

独立試行の確率

独立試行T=(T1、T2)において

T1では事象Aが起き、
T2では事象Bが起きる事象をCとする。

公式

\( P(C) = P(A)P(B) \)

が成り立つ。

３つ以上の試行についても同様である。

反復試行

同じ試行を、何回か繰り返し行う試行を

”反復試行”という。

反復試行の確率

ある試行において事象Aの起きる確率をpとする。

この試行をn回繰り返し行った時、
事象Aがちょうどr回起きる確率は

\( {}_n \mathrm{C}_r p^r (1-p)^{n-r} \quad (= {}_n \mathrm{C}_r p^r q^{n-r} ) \)

である。

ここでqは事象Aが起きない確率、q=1-pです。

期待値

試行の結果により値の定まる変量Xについて、

Xのとりうる値は全部で

x1、x2、…、xnであり

それぞれの起きる確率は

p1、p2、…、pnとする。
（p1+p2+…+pn=1）

この時

\( E = x_1 p_1 +x_2 p_2 + \cdots +x_n p_n \)

を

Xの”期待値”または”平均値”という。

条件つき確率

ある事象Aが起きた場合の、別の事象Bの起きる確率を

”条件つき確率”といい

\( P_A (B) \)

と書く。

公式

各根元事象が同様に確からしい試行の標本空間をUとする。

二つの事象A、Bについてn(A)≠０の時、

条件つき確率PA(B)は

Aを新たな標本空間とした場合の
A∩Bの起きる確率と考えられる。

よって、

$$ P_A(B) = \frac{n(A \cap B)}{n(A)} = \frac{P(A \cap B)}{P(A)} \hspace{20cm} $$

確率の乗法定理

上の公式の分母を払うと

定理

\( P(A \cap B) = P(A)P_A(B) \)

積事象の確率から条件つき確率が求まり、
条件つき確率から積事象の確率が求まります。

独立

事象Aの発生の有無が
事象Bの起きる確率に何も影響を与えない、

すなわち

\( P_A (B) = P(B) \)

の時、

事象Bは事象Ａに”独立”である、という。

独立事象の乗法定理

P(A)≠０かつP(B)≠０であれば

  • 事象Aと事象Bは互いに独立
  • \( P(A \cap B) = P(A)P(B) \)

は同値。

上の定理をすべての場合に成り立たせるため、

P(A)=０またはP(B)=０の時も便宜上
事象Aと事象Bは互いに独立であると見做す。

従属

二つの事象が独立でないことを

”従属”という。

余事象と独立

AとBが独立とは、

Aが起きても起きなくても
Bの起きる確率は同じ、ということである。

よってAの余事象とBも独立になる。

次はすべて同値。

  • \(A\)と\(B\)は独立
  • \(\overline{A}\)と\(B\)は独立
  • \(A\)と\(\overline{B}\)は独立
  • \(\overline{A}\)と\(\overline{B}\)は独立

３つの事象の独立

事象A、B、Cの内どの二つも互いに独立で

どの二つの事象の積事象も残りの一つと独立な時

A、B、Cは”独立”である、という。

独立ならば

\( P(A \cap B \cap C) = P(A)P(B)P(C) \)

が成り立つ。
（逆は成り立ちません）

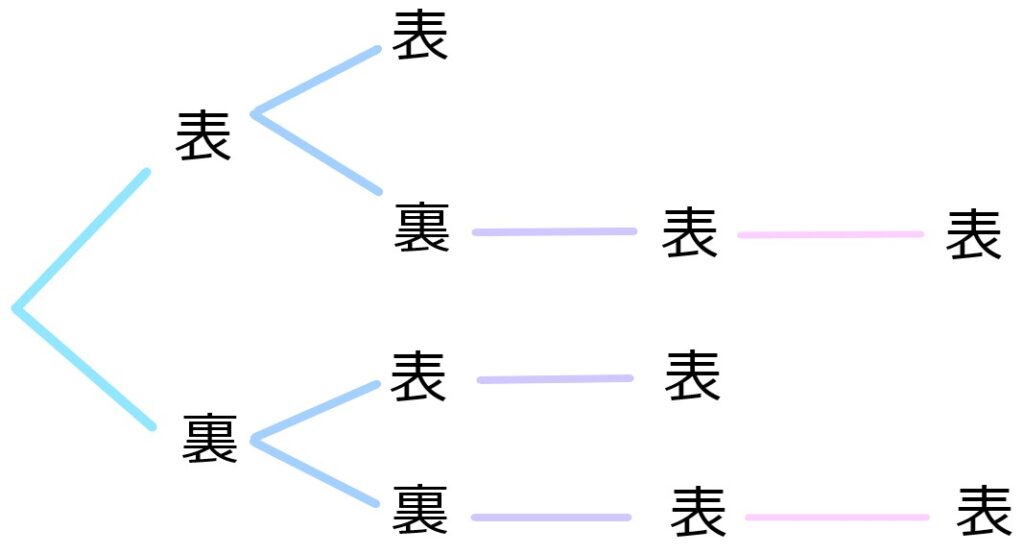
樹形図の利用

複数回に跨る試行の結果を、

樹形図を用いて整理すると
確率を計算しやすくなることがある。

（例）コインを４回投げた時、表が２回連続で出る確率。

以上で、第１巻の勉強は全てです。

前の単元

単語帳トップへ

-高校数学の単語帳１巻