
集合と場合の数
集合の要素の個数
要素の個数が有限である集合を
”有限集合”といい、
無限に多くの要素を持つ集合を
”無限集合”という。
有限集合Aの要素の個数を
\( n(A) \)
と書く。
場合の数
ある事柄の起きる場合をすべて、
もれなく、重複することなく
数え上げたものを
”場合の数”という。
樹形図
例えば、
集合U={a, b, c, d}の部分集合が
3つの要素から成る場合の数を求めたい。
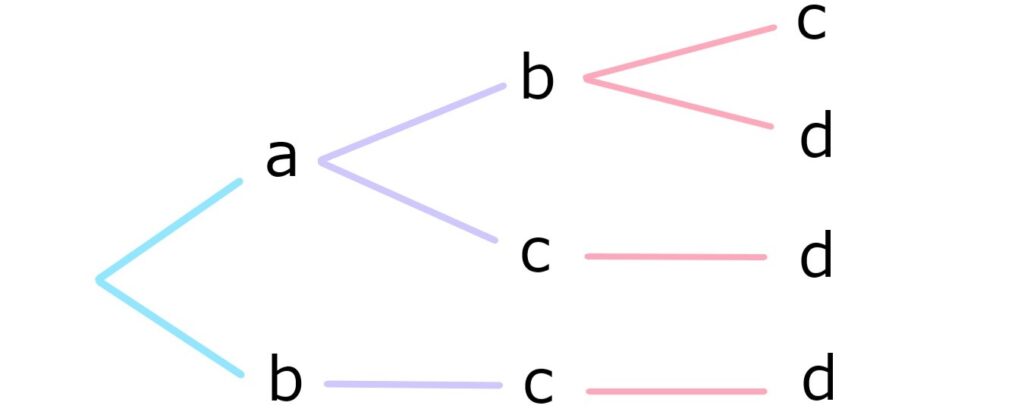
上の様なアルファベット順に
枝分かれする図を考えると数えやすい。
これを”樹形図”という。
和の法則
二つの事柄AとBは同時には起こらないとする。
Aの起こり方がp通り、
Bの起こり方がq通り、ならば
AかBのどちらかが起こる場合の数はp+q通りである。
式で表現
これは、
集合Aを事柄Aの起こる場合全体、
集合Bを事柄Bの起こる場合全体、とした時
\( A \cap B = \phi \)
ならば
\( n(A \cup B) = n(A) +n(B) \)
が成り立つことと一緒である。
積の法則
二つの事柄AとBについて
Aの起こり方はp通り、
その各々について
Bの起こり方がq通りずつあるならば
AとBが共に起こる場合の数はpq通りである。
直積(予備知識)
二つの集合AとBについて、
Aの要素aとBの要素bの
順序を考えた組(a, b)の全体が作る集合
\( \{ (a, \; b) | a \in A, \; b \in B \} \)
を
AとBの”直積”といい
\( A \times B \)
と書く。
式で表現
積の法則は特に
\(q = n(B) \)
である時
\( n(A \times B) = n(A) n(B) \)
を意味する。
順列
何個かのものを
順序を付けて一列に並べた配列を、
それらの”順列”という。
順列の個数
n個の異なるものから、
異なるr個を取って並べた順列の総数を
\( {}_n \mathrm{P}_r \)
と書く。
公式
\( {}_n \mathrm{P}_r = n(n-1)(n-2) \cdots (n-r+1) \)
階乗
異なるn個のものの順列の総数nPnを
nの”階乗”といい
n!と書く。
\( n! = n(n-1)(n-2) \cdots 3 \cdot 2 \cdot 1 \)
である。
0の取り扱い
階乗を使うとnPrは
$$ {}_n \mathrm{P}_r = \frac{n!}{(n-r)!} \hspace{20cm} $$
とも書ける。
r=nの時(0の階乗)
特にr=nならば
$$ {}_n \mathrm{P}_n = \frac{n!}{0!} \hspace{20cm} $$
左辺はn!なので、
等式を成り立たせるため
0の階乗は形式的に
\( 0! = 1 \)
と定められる。
r=0の時
また、r=0ならば
$$ {}_n \mathrm{P}_0 = \frac{n!}{n!} \hspace{20cm} $$
右辺は1なので
\( {}_n \mathrm{P}_0 = 1 \)
とも定められる。
円順列
何個かのものを円形に並べた配列を
”円順列”という。
異なるn個のものの円順列の総数は(n-1)!である。
重複順列
異なるn個のものから
重複を許してr個取り出した順列を
”重複順列”という。
その総数はnrである。



