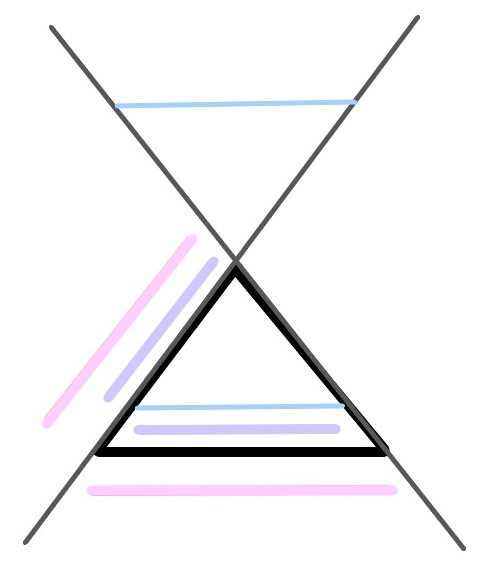高校数学の単語帳２巻

【数学A】「平面図形」三角形の性質の単語帳

三角形の性質

三角形において次が成り立つ。

辺と角の大小

定理１

大きい辺に対する角は、小さい辺に対する角より大きい。

角と辺を入れ換えた主張も正しい。

定理２

大きい角に対する辺は、小さい角に対する辺より大きい。

証明

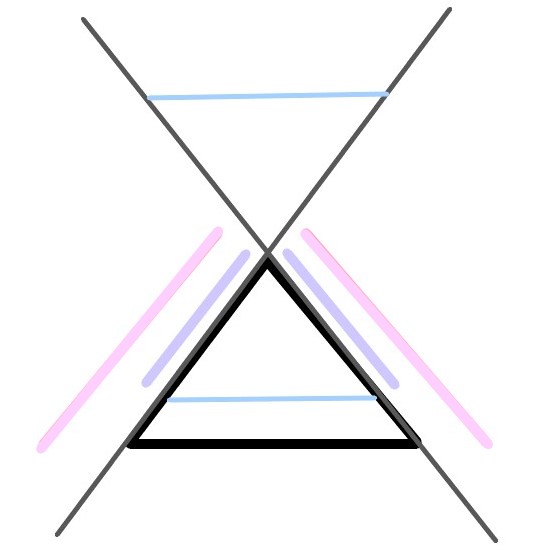
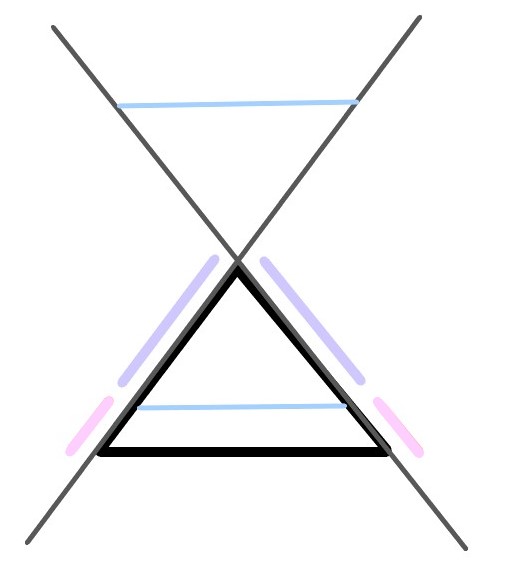
AB>ACとする。

補助線を引き、

ACを一辺に持つ二等辺三角形を作れば自明。

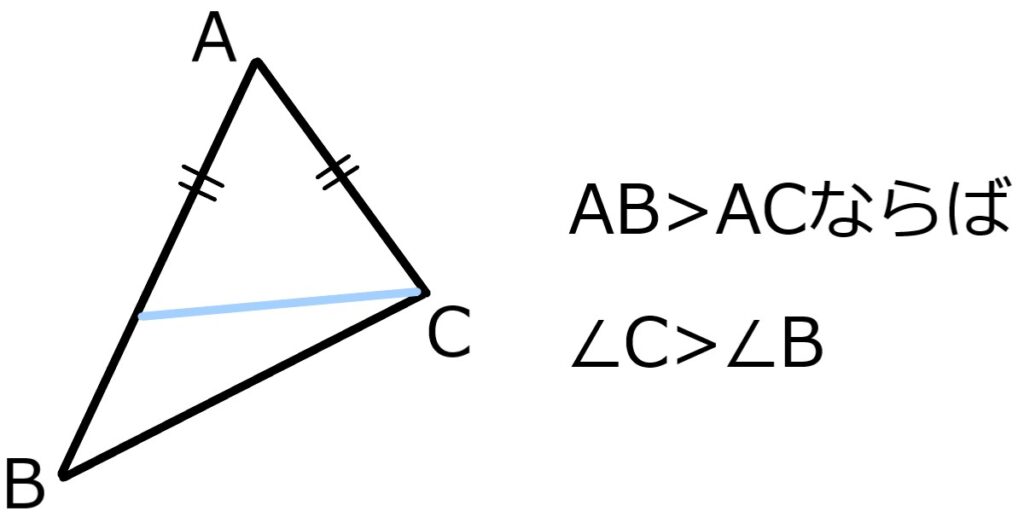
定理２は背理法で示される。

すなわち∠C>∠Bであるのに、

AB≦ACであった時を考える。

AB<ACなら定理１に矛盾し、
AB=ACであれば二等辺三角形より∠C=∠B　\(\square\)

２辺の和と差

定理３

２辺の長さの和は、他の１辺の長さより大きい。

また、

定理４

２辺の長さの差は、他の１辺の長さより小さい。

証明

辺BAの延長上に点Dをとり、二等辺三角形ACDを作る。

定理２を使うとBD>BC

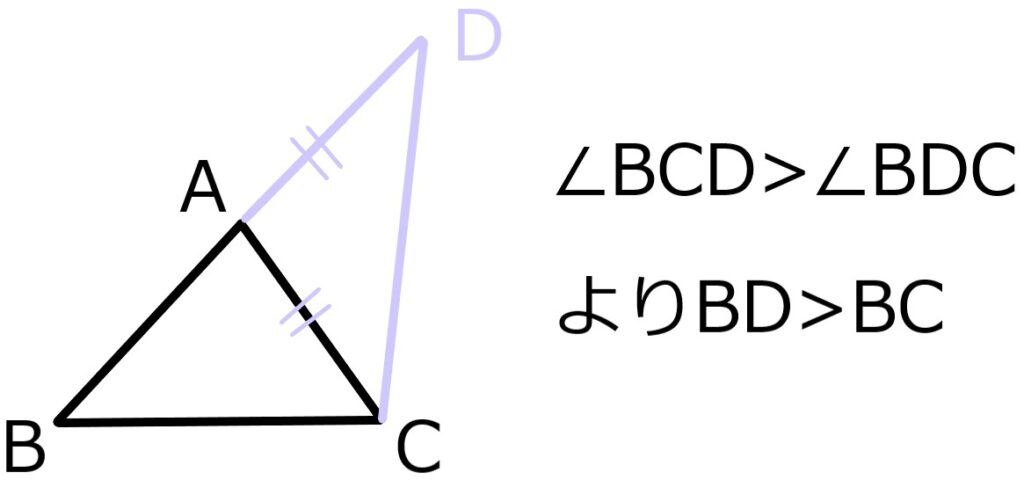
ここでBD=AB+ACなので示された。

定理４は背理法から、
すなわちAB-AC≧BCを仮定し矛盾を導く。

両辺にACを足すと
AB≧BC+ACなので定理３に反する。\(\square\)

Pを三角形ABCの内部の点とすれば
AB+AC>PB+PCである。

証明

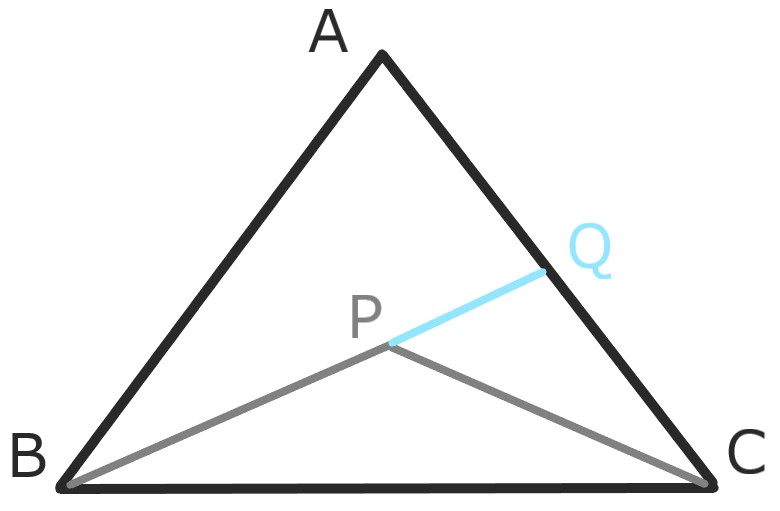
BPの延長と辺ACの交点をQとする。

定理３より

PQ+QC>PC

と

AB+AQ>BQ

を得る。

両辺を足して

AB+(AQ+QC)+PQ>BQ+PC

AB+AC+PQ>(PB+PQ)+PC

両辺からPQを引いて示される。\(\square\)

三角形の存在条件

先の定理より、
三角形の３辺の長さa、b、cは次を満たす。

\( |b-c| < a < b+c \)

逆に正の数a、b、cが上の不等式を満たすなら

これらを３辺の長さに持つ三角形が存在する。

証明

０<θ<180について、

２辺の長さがb、cで
その間の角度がθの三角形は存在する。

三角形の残りの１辺の長さaは、
θに応じて|b-c|からb+cまでの値をとる。\(\square\)

反射の最短距離

直線l上の点PでAP+PBを最小にするものを求めたい。

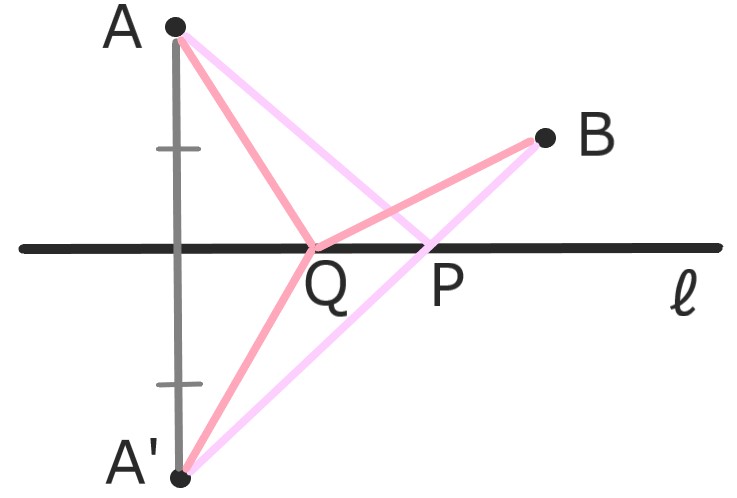
lを軸に点Aと対称の位置に点A’をとる。

A'Bとlの交点が求める点Pである。

証明

l上に点Pでない点Qをとる。

△QA'Bに定理３を適用すればA'Q+QB>A'B

対称性より

A'Q+QB=AQ+QB

A'B=AP+PB

なので示される。\(\square\)

領域内最小の三角形

鋭角XOYの間に点Pがある時、

△PQRの周PQ＋QR＋RPが
最小となる様に点Q、RをOX、OY上にとりたい。

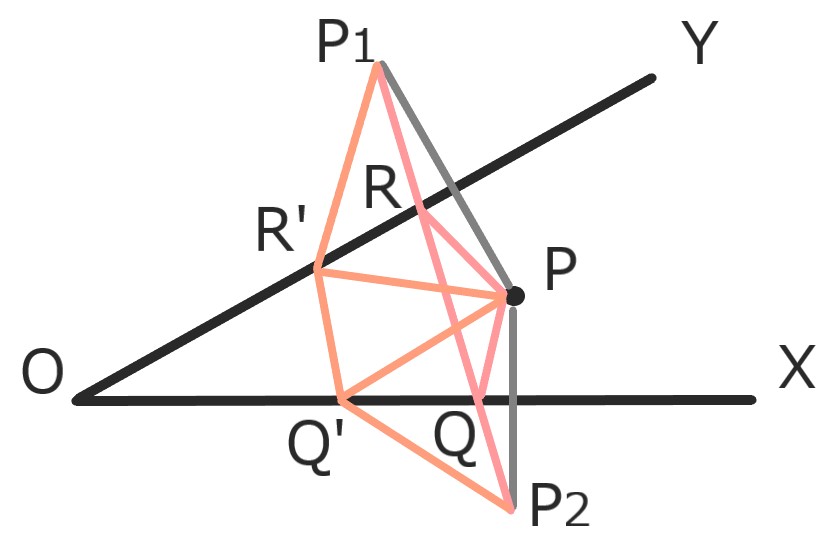
OXとOYについてPと対象の点をP2、P1とし
P2P1とOX、OYとの交点をQ、Rにすれば良い。

証明

点Q'、R'をQ、Rとは異なる点とする。

対称性より

PQ+QR+RP=P2Q+QR+RP1
PQ'+Q'R'+R'P=P2Q'+Q'R'+R'P1

Q'とR'からP2P1に垂線を降ろして考えれば

P2Q+QR+RP1<P2Q'+Q'R'+R'P1　\(\square\)

平行線と線分の比

三角形ABCにおいて
BA、CAの延長上に点B'、C'をとる。

P、Qを半直線AB、AC上または

AB'、AC'上の点とした時、次が成り立つ。

定理５-１

$$ \mathrm{PQ} /\!/ \mathrm{BC} \Leftrightarrow \frac{\mathrm{AP}}{\mathrm{AB}} = \frac{\mathrm{AQ}}{\mathrm{AC}} $$

定理５-２

$$ \mathrm{PQ} /\!/ \mathrm{BC} \Leftrightarrow \frac{\mathrm{AP}}{\mathrm{PB}} = \frac{\mathrm{AQ}}{\mathrm{QC}} $$

定理５-３

$$ \mathrm{PQ} /\!/ \mathrm{BC} \Rightarrow \frac{\mathrm{AP}}{\mathrm{AB}} = \frac{\mathrm{PQ}}{\mathrm{BC}} $$

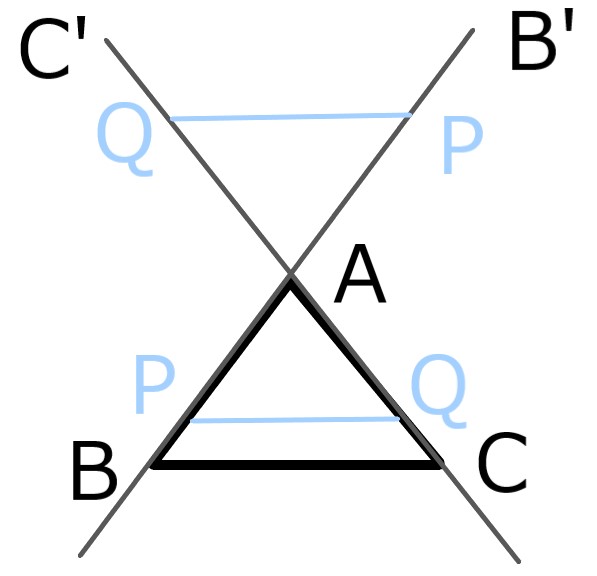
これらは、PQがBCと平行であれば
長さの比が等しくなることを言っている。

ただし定理5-3だけ逆は成り立たない。

反例

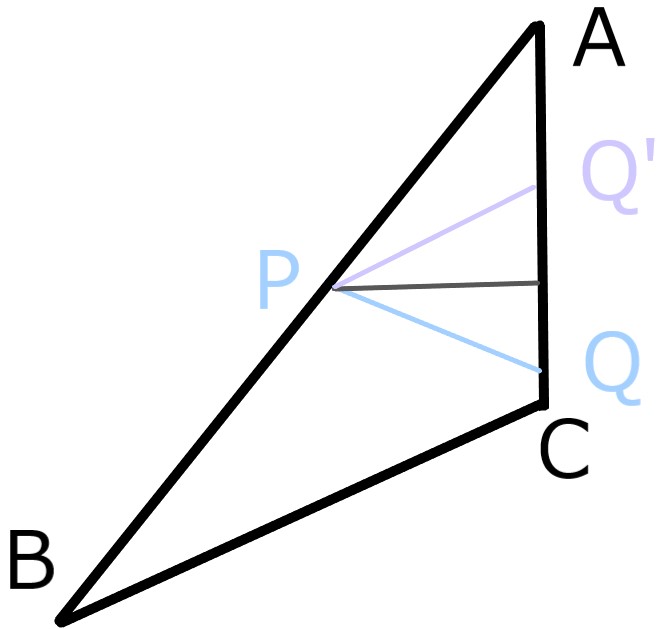
PQ'//BCである様に点P、Q'をとり

PからACに降ろした垂線
について対象の位置に点Qをとる。

この時PQ=PQ'である。

定理5-3よりAP/AB=PQ'/BCなので

AP/AB=PQ/BC

しかしPQ//BCでない。\(\square\)

線分

m、nを正の数とする。

内分点

線分AB上の点Pが

\( \mathrm{AP} : \mathrm{PB} = m : n \)

を満たす時、

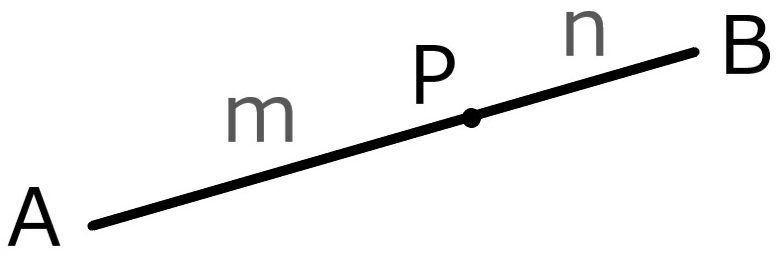
PはABをm:nに

”内分”するといい、

Pを

”内分点”という。

外分点

ABの延長上の点Qが

\( \mathrm{AQ} : \mathrm{QB} = m : n \)

を満たす時、QはABをm:nに

”外分”するといい、

Qを

”外分点”という。

ただしm≠nとする。

外分点の位置は
mとnの大小関係に次の通り従う。

m>nの場合

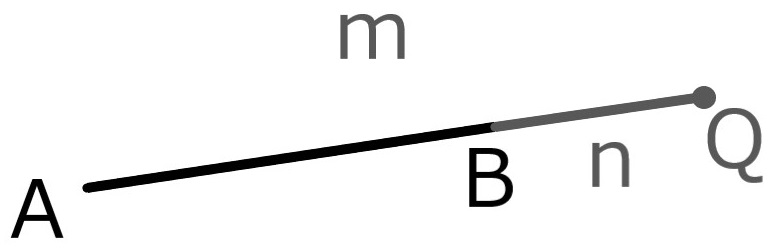
m<nの場合

角の二等分線と比

三角形ABCの角の二等分線について次が成り立つ。

定理６-１

∠Aの二等分線とBCとの交点Pは、BCをAB:ACに内分する。

証明

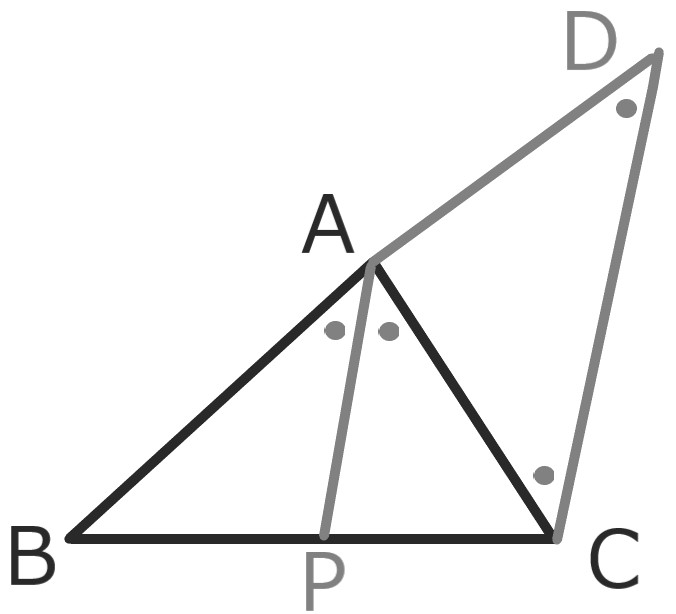
ABの延長上に点DをAP//DCである様とれば、
△ADCは二等辺三角形である。

よってAD=AC

また△BPAと△BCDは相似なので

BP:PC=AB:AD=AB:AC　\(\square\)

さらにAB≠ACならば

定理６-２

∠Aの外角の二等分線とBCの延長との交点Qは、
BCをAB:ACに外分する。

証明

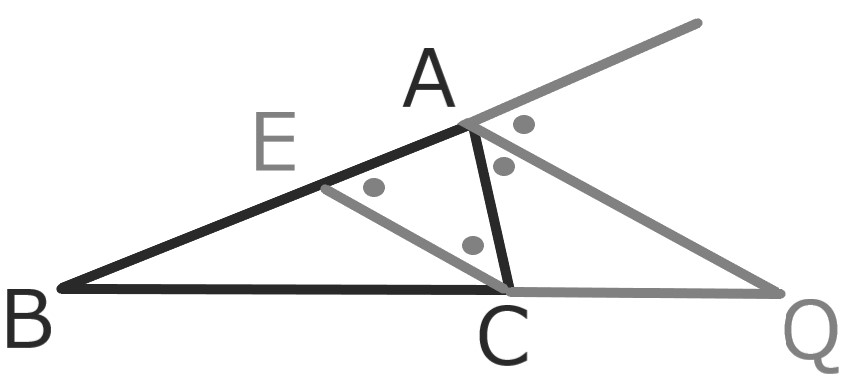
AB上に点EをEC//AQである様とれば、
△AECは二等辺三角形である。

よってAE=AC

EC//AQより△BCEと△BQAは相似なので

BQ:QC=AB:AE=AB:AC　\(\square\)

次の単元

単語帳トップへ

-高校数学の単語帳２巻