【数学の使い道】
高校数学までの身近な例まとめ（小学校）

数学（と算数）は学校で勉強するものの、
使い道がよく分からない科目です。

私も今まで京都大学の院を卒業するまで、
友達や家族から

と何度も聞かれて来ました。

なので、高校数学までの実際の使われ方を
解説することにしました。

数学の勉強は小学校、中学校、高校、そして大学の順に、
始めは日常生活で役に立つ計算から、
段々と科学の舞台で役に立つ高度な定理へと進んで行きます。

一般の人たちは算数と中学数学の習得で十分ですが、
科学者にとっては大学数学まで必要。

科学者でない人も、科学技術という形で
例えば身近な車、パソコン、その他の多くの
発明品を通じて、遠回しに数学の恩恵にあずかっています。

この記事では、算数の使い道について解説します。

（中学校、高校数学の使い道は、現在執筆中です）

単元「データの活用」の使い道は明らかなので説明を省略します。

算数の使い道

小学校で習う算数の大きな目的は、

お金の計算をできるようにすること

と言って良いでしょう。

貨幣経済においては、
お金の計算ができないと生きていけません。

また、私たちの住んでいる世界を
図形的に捉える能力も大事です。

目的地までの移動は距離、方向の認識のおかげで出来、

身の回りの物の多くは三角形、四角形、円として見れます。

それらの長さ、面積、体積を理解することで
物の大きさを比較できて、

例えば家から最も近いスーパーに行って、
なるべく大きなりんごを買って来れます。

さらには数量は、

• 時・分・秒
• 角度
• メートル
• グラム

等の単位により分類できることを学び、

測定した様々な値は、表、グラフにまとめることで、
わかりやすくなります。

このように、日常生活とつながる
数学的テクニックが詰まっています。

ここからは単元ごとに、イラスト付きで詳しく説明します。

数と計算

数の数え方を勉強して、
それらの四則演算をできるよう目指します。

自然数の数え方

１、２、３、から始めて、大きな数は

十、百、千、万、億、兆

といった単位を用いることで表せます。

概数

という風に、概数で数字を簡単に見られます。

概数を求める手法として四捨五入も習います。

小数、分数

例えば、１と２の間の数は

小数なら

\( 1.5 \)

分数なら

$$ \frac{3}{2} \hspace{20cm} $$

です。

自然数より細かく数を認識できます。

四則演算

これらの数の

• 足し算
• 引き算
• かけ算
• 割り算

をできるようにします。

この能力が日常生活でもっとも重要と言えるでしょう。

偶数・奇数

２で割り切れるか、つまり半分こ
できるか考えます。

約数・倍数

発展して３で割り切れるか、４で割り切れるか、
なども考えます。

図形

基本的な図形を勉強して、
それらの長さ、面積、体積、角度を計算します。

私たちの身の回りの物が
どれくらいの大きさなのか、
長さ、面積、体積で理解して、

どちらの方向にあるか、を角度で知ることができます。

方向・位置

物の位置、どちらの方向にあるか、
という概念を学びます。

日常生活でよく見る物の形に名前を付けます。

三角形

正三角形

二等辺三角形

四角形

正方形

長方形

平行四辺形

ひし形

台形

多角形

円

円の周、面積を求めるため円周率も習います。

円周率≒3.14

３次元

立方体

直方体

角柱

円柱

球

実際の物の形はもっと複雑ですけど、

単純化するなら上記の図形、または
それらの組合せです。

図形の性質

これらの間に成り立つ関係についても勉強します。

物作りのヒントになることが多いです。

平行

完全に同じ方向であること。

例えば道路は歩道、車道が平行になるよう作られます。

垂直

完全に異なる方向であること。

例えば家のかべ、柱は地面に垂直に建てられます。

合同

完全に同じ図形であること。

縮図、拡大図

大きくしたり小さくすれば同じな図形。

対称（線対称・点対称）

鏡写しにしたり、
点を中心に回転させれば同じな図形。

測定・変化と関係

メートル、グラム、などの単位を勉強して、
物の量を測定する能力を手に入れます。

また、グラフや比を通じて、
２つの量の間に成り立つ関係も考察します。

単位

時刻

時間は時・分・秒、で表されます。

長さ、広さ、かさ

長さ	mm	cm	m	km
広さ	mm2	cm2	m2	km2
かさ	mm3	cm3	m3	km3

容積

\( \mathrm{mL}, \, \mathrm{dL}, \, \mathrm{L} （リットル） \)

重さ

\( \mathrm{g}, \, \mathrm{kg}, \, \mathrm{t} （トン） \)

１トン＝1000キログラム

速さ

時速、分速、秒速。

比例関係

これらの量の間の関係に気付くと、
物事の見通しが良くなります。

例えば、時速30kmで走る車のグラフを描くと、
次の比例関係が成り立っています。

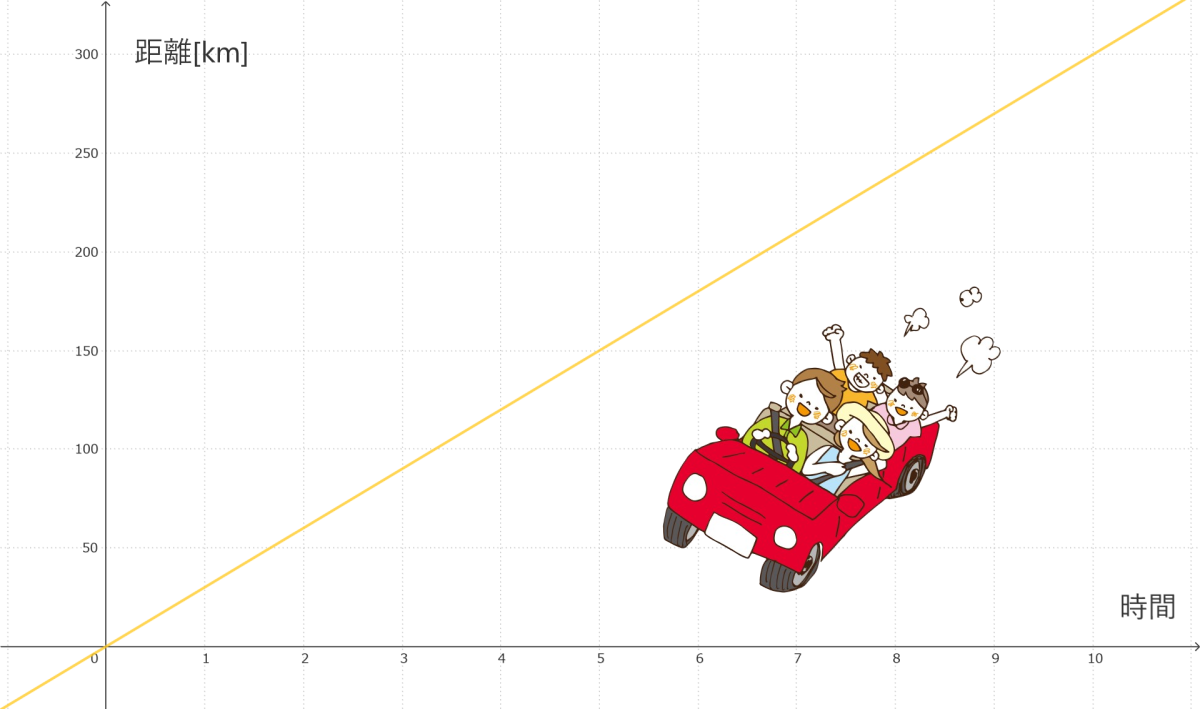
反比例

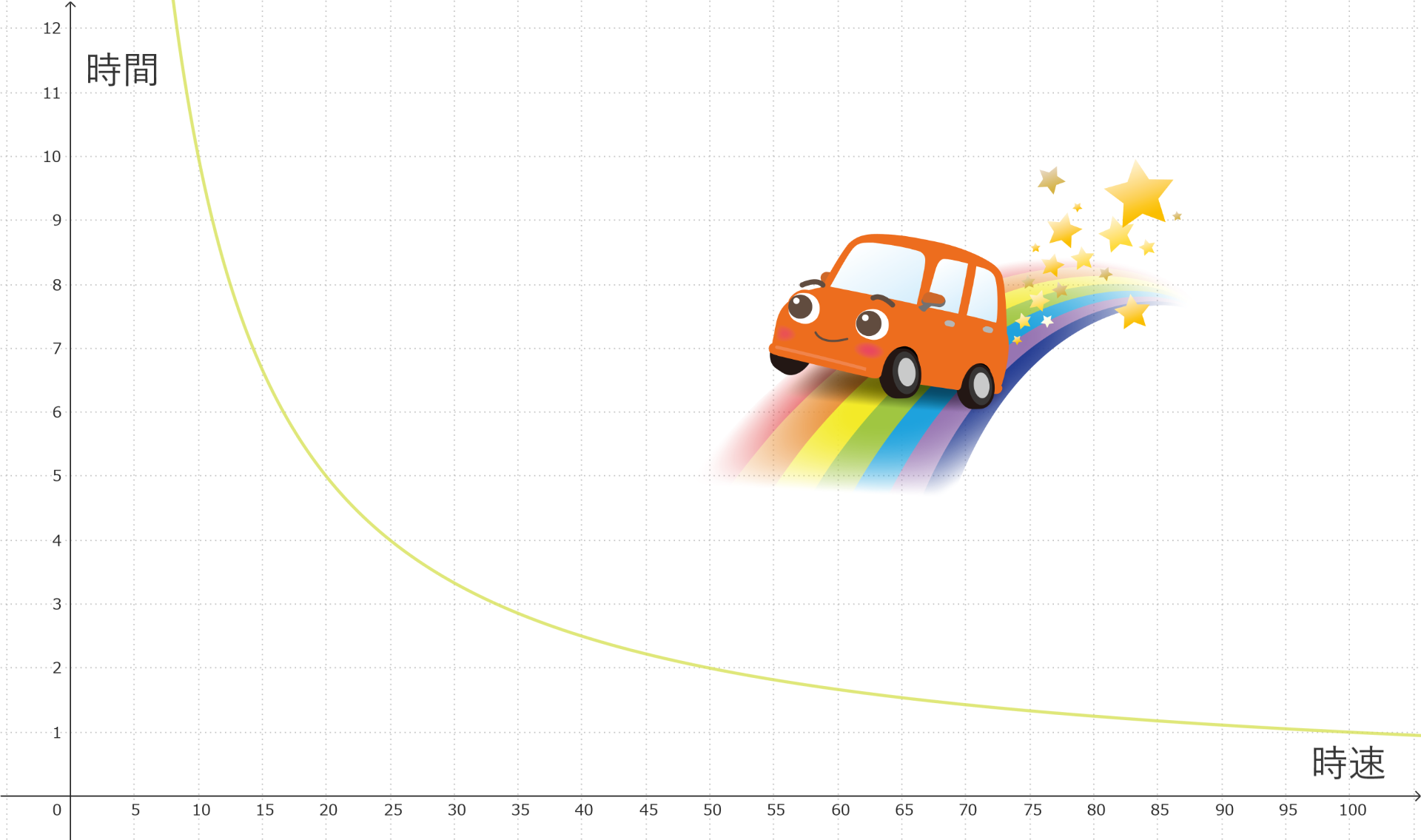
また、100kmの距離を車で走る際の
速さと時間の関係は反比例になります。

割合

全体の何％を占めるか、
という割合の概念も便利です。

コップに半分（50%）水を注いだり、

クラスメートの７割が賛成してくれている、

等の見方ができます。

比

割合は基準となる全体量があるのに対して、
基準を設けず、そのまま見比べるのが比です。

料理をする時に、牛乳と砂糖を２：３で混ぜたり、

50分勉強したら10分休む、
５：１のペース配分で頑張ったり、

複数の量を相互関係で管理できます。

まとめ

算数を勉強すると、

• お金等の計算能力
• 世界を図形的に捉える能力
• 単位を用いて数量を測定する能力

の３つが手に入ります。

これらは私たちの日常生活を
根本から支えてくれます。

【まとめ】日常生活で使う算数の例
【生活に算数を活かす】

小学校で習った算数。 習ったものの肝心な使い道が良くわからなくて困っている人も多いと思います。 そこで、単元ごとに日常生活での例をまとめてみました。 算数を生活に活かすヒントにご活用ください。 基本の ...