
教科書に載っている余弦定理は、
三角形を鋭角、直角、鈍角に分けて
導出するので証明が長くなりがちです。
発展した解き方として
極座標、ベクトルの知識を用いれば
証明を一本化できるので
詳しく説明したいと思います。
余弦定理の極座標による証明
公式、
$$a^2 = b^2 + c^2 - 2bc \cos∠A$$
を示します。
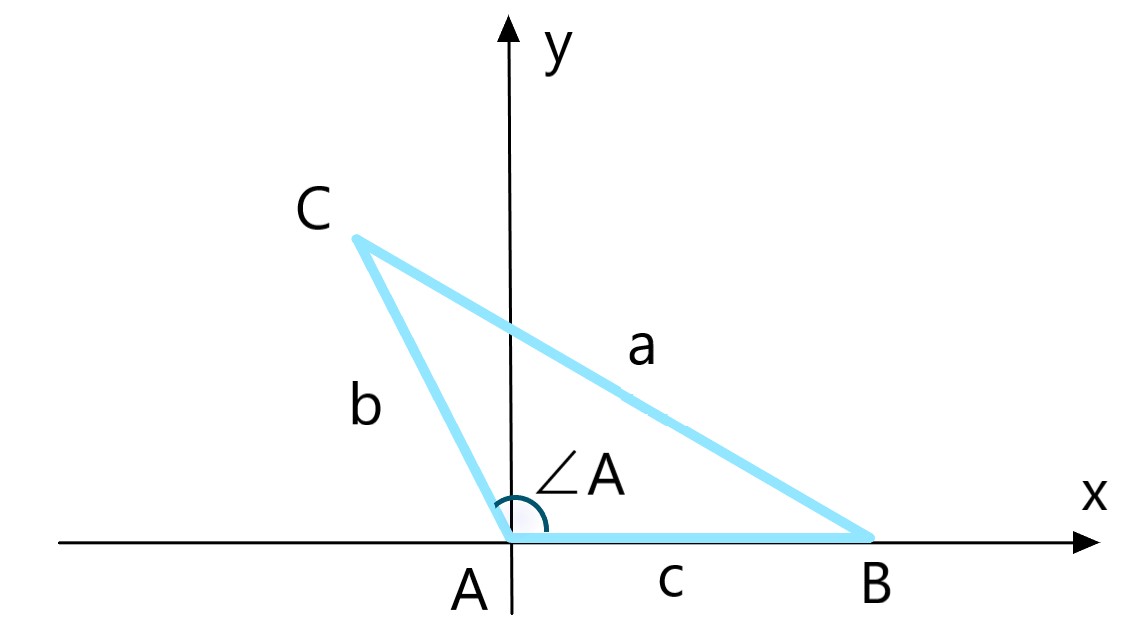
三角形ABCを点Aが原点に辺ABがx軸に沿う様に置きます。
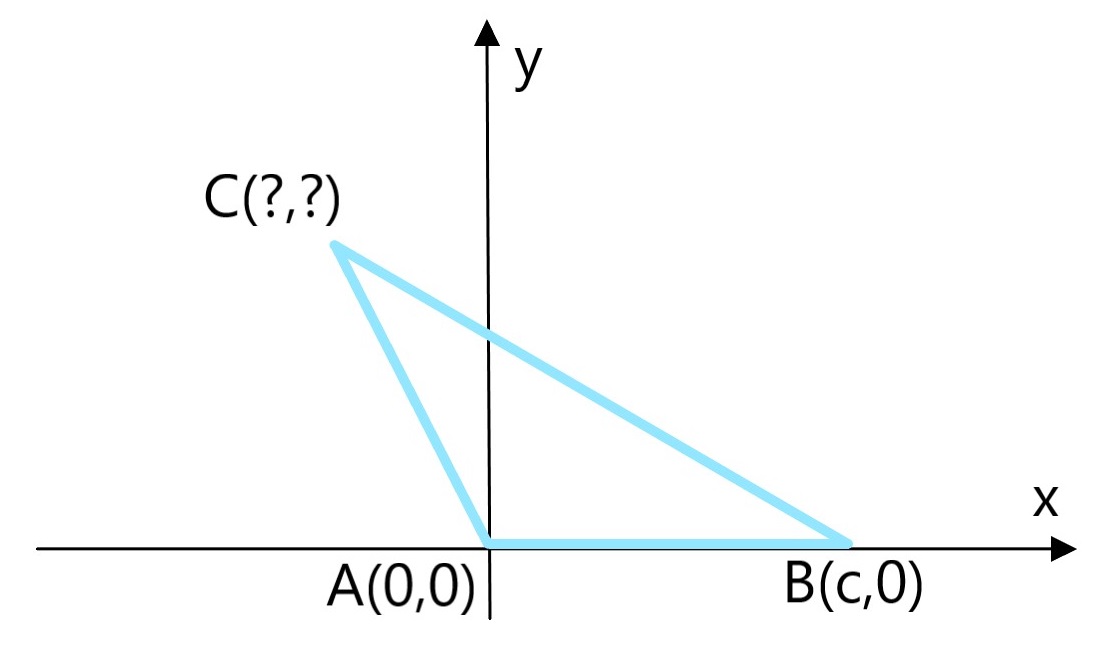
点Aの座標は(0,0)、Bは(c,0)とすぐに分かりますが、
点Cの座標は求めづらい位置にあります。
通常は三角形を鋭角、直角、鈍角に場合分けして
点Cの座標を求めますが、極座標を使えば簡単です。
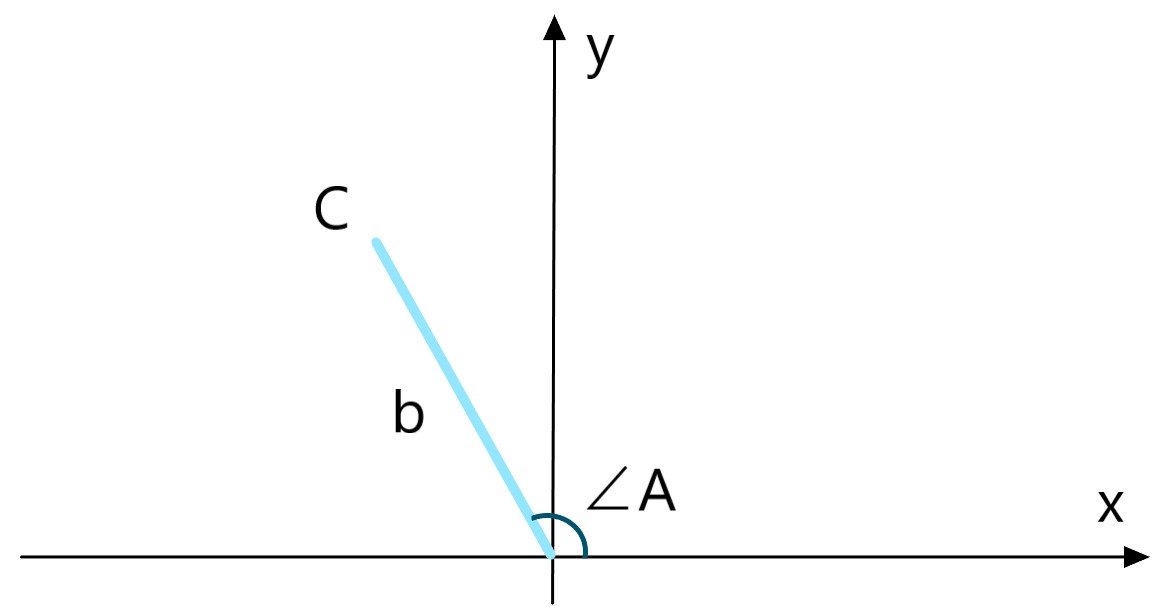
距離b、偏角∠Aの位置に点Cはあるので
直交座標への変換公式より座標は(bcos∠A,bsin∠A)です。
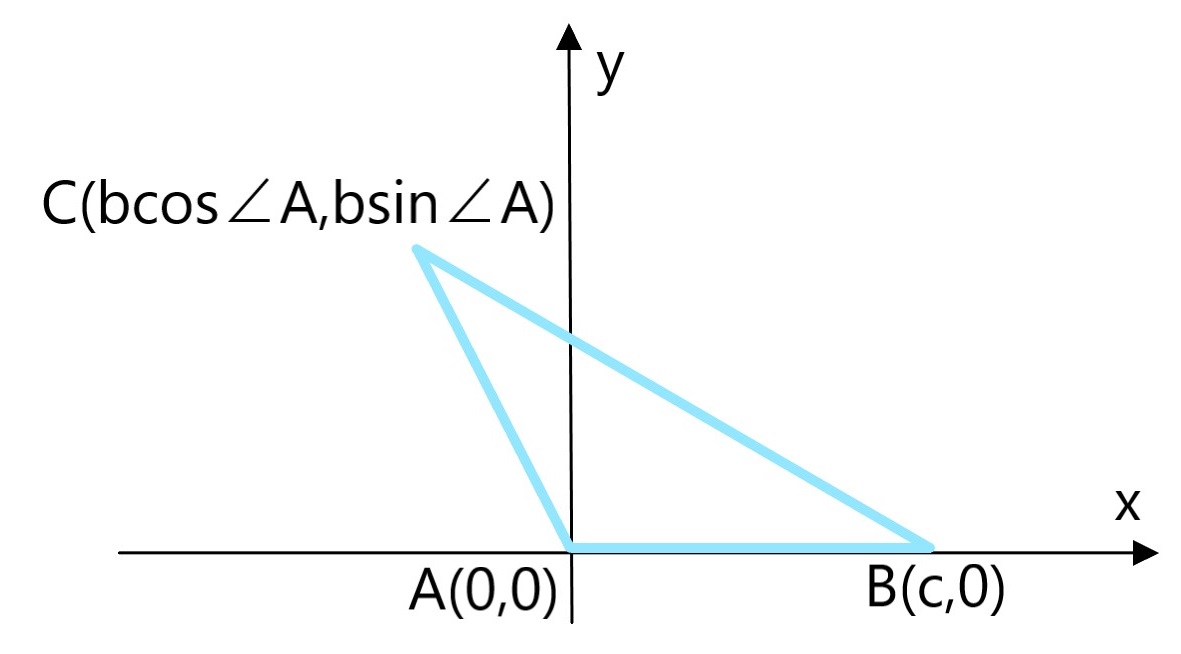
まとめると上図の通り
すべての点の座標が求まりました。
座標が分かればベクトルを使えます。
$$\overrightarrow{\mathrm{AB}}=\begin{pmatrix} c \\ 0 \end{pmatrix} \quad \overrightarrow{\mathrm{AC}}=\begin{pmatrix} b \cos ∠A \\ b \sin ∠A \end{pmatrix} \hspace{20cm}$$
なので
$$\overrightarrow{\mathrm{BC}} = \overrightarrow{\mathrm{BA}} + \overrightarrow{\mathrm{AC}} =\begin{pmatrix} -c + b \cos ∠A\\ b \sin ∠A \end{pmatrix} \hspace{20cm}$$
です。
これより、
\(a^2 = |\overrightarrow{\mathrm{BC}}|^2 = (-c + b \cos ∠A)^2 + (b \sin ∠A)^2\)
と書けて
bの二乗で括り三角関数の公式を適用すれば
\( = c^2 - 2bc \cos ∠A +b^2(\cos^2 ∠A + \sin^2 ∠A) \)
\(= b^2 + c^2 - 2bc \cos∠A\)
以上より、余弦定理
\(a^2 = b^2 + c^2 - 2bc \cos∠A\)
を証明できました。\(\square\)
まとめ
極座標なら三角形の種類に依らず
頂点の座標を一律に表せる、
という特性を利用しました。
