
数学Ⅰ「数と式」の忘れがちな
単語と定理を見直せるページです。
一通り勉強が済んだ後の復習用にお使い下さい。
単項式
\( 3abx^2 \)の様に、
いくつかの文字または
数の掛け合わせで作られる式を”単項式”という。
係数・次数
単項式の数の部分を”係数”、
掛け合わせる文字の個数を”次数”という。
例えば\(3abx^2 \)について、
係数は3、次数は4である。
特にxに着目し
その他の文字を数と同様に扱うなら
係数は3ab、次数は2である。
多項式
いくつかの単項式の和で作られる式を”多項式”という。
その各単項式を多項式の”項”という。
整式
多項式を”整式”ということもある。
同類項
文字の部分が同じである項を”同類項”という。
多項式の同類項をまとめた際、
各項の次数の中で最大のものを
その多項式の”次数”という。
因数分解
一つの多項式Aを、
1次以上の多項式B、C、...、の積の形に
書き直すことをAを”因数分解”するという。
また、BやCをAの”因数”という。
共通因数
複数の多項式に共通で現れる因数のこと。
多項式の約数、倍数
多項式Aが多項式Bで割り切れる時
BをAの”約数”、AをBの”倍数”という。
公約数・公倍数
複数の多項式に共通の約数を
それらの”公約数”、
共通の倍数を”公倍数”という。
最大公約数・最小公倍数
公約数の中で、
次数の最も高いものを特に”最大公約数”
公倍数の中で、
次数の最も低いものを”最小公倍数”という。
下の例において
\(A=2(x+1)(x+3) \quad B=x(x+1)(x+2) \)
最大公約数はx+1、
最小公倍数はx(x+1)(x+2)(x+3)である。
*多項式の約数、倍数では
単なる数の因数は無視されます。
剰余の定理
多項式P(x)を1次式(x-α)で割った時の余りはP(α)である。
因数定理
「1次式(x-α)が多項式P(x)の因数」\(\Leftrightarrow\)「P(α)=0」
分数式
A、Bが二つの多項式で、Bが文字を含む時、
\( \frac{A}{B} \)の形に表される式を”分数式”という。
またBをその”分母”、Aを”分子”と呼ぶ。
約分
分数式の分母、分子をそれらの
共通因数で割ることを”約分”という。
既約分数式
分母、分子が共通因数を持たず、
それ以上約分できない分数式を”既約分数式”という。
計算テクニック
始めに分数式の分子を分母で割ると、
計算しやすくなることがある。
$$\quad \frac{x^2 + 2x + 2}{x + 1} + \frac {-x^2 -2x + 2}{x + 2} + \frac{-x}{x + 3} \hspace{20cm}$$
$$= \left( x + 1 + \frac{1}{x + 1} \right) + \left( -x + \frac{2}{x + 2} \right) + \left( -1 + \frac{3}{x + 3} \right) \hspace{20cm}$$
$$= \frac{1}{x + 1} + \frac{2}{x + 2} + \frac{3}{x + 3} \hspace{20cm}$$
有理式
多項式と分数式を合わせて”有理式”という。
有理式の和差積商もまた有理式である。
数直線
”数直線”は次の様に作られる。
- 直線上に異なる2点O、Eをとる。
- O以外の点Pについて、
OEの長さを単位としたOPの長さをaとする。 - 点PがOに関してEと、
- 同じ側にある時はaを
- 反対側にある時は-aを点Pに対応させる。
- 点Oには0を対応させる。
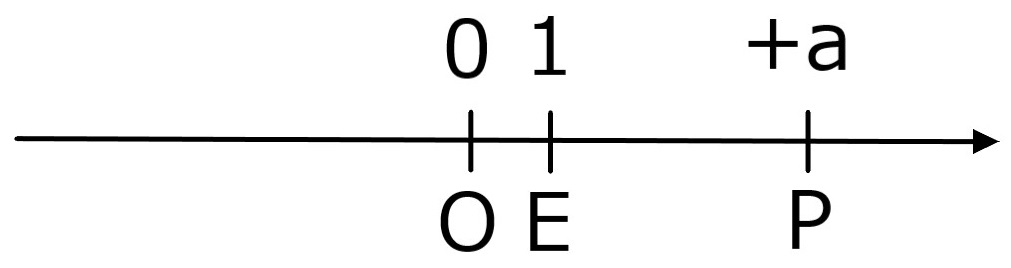
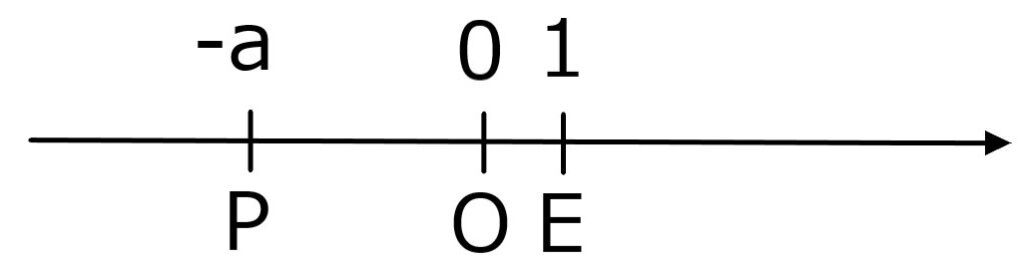
点Oを”原点”、Eを”単位点”という。
平方根
2乗するとaになる数を、aの”平方根”という。
正の数aの平方根は、
正負の二つあり正の平方根を√aと書く。
また0の平方根は0であり、√0=0と定める。
記号√を”根号”という。


