
不等式
範囲の書き方
例えば-1<x≦2を数直線上に書くと次の様になる。
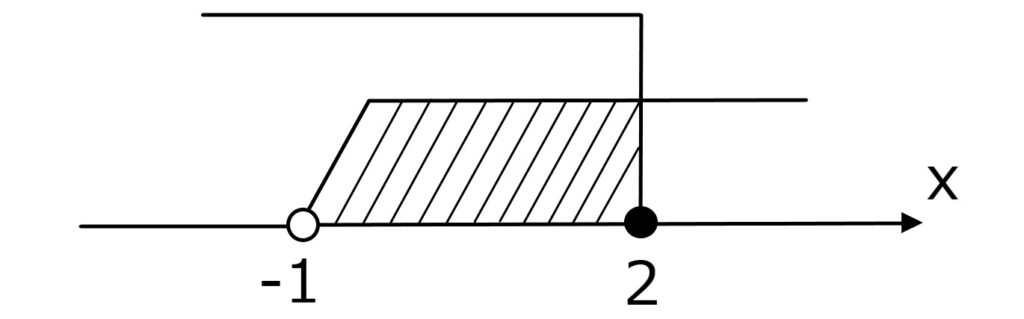
- 端点が範囲に含まれない時は、
白丸で表し斜めに線を伸ばして範囲を示す。 - 端点が範囲に含まれる時は、
黒丸で表し垂直に線を伸ばして範囲を示す。 - 範囲は斜線で塗りつぶす。
2次方程式
移項して整理すると次の形、
ax2+bx+c=0(a、b、cは定数でa≠0)
になる方程式を
xについての”2次方程式”という。
これの実数の解を”実数解”、虚数の解を”虚数解”という。
(複素数の正確な定義は後述)
解の公式
2次方程式ax2+bx+c
(a、b、cは実数でa≠0)は次の様な解をもつ。
$$x=\frac{-b \pm \sqrt{b^2 - 4ac} }{2a} \hspace{20cm} $$
証明
$$\quad ax^2 + bx + c = 0 \hspace{20cm} $$
$$\Leftrightarrow x^2 + \frac{b}{a} x = -\frac{c}{a} \hspace{20cm} $$
$$\Leftrightarrow x^2 + \frac{b}{a} x + \left( \frac{b}{2a} \right) ^2 = \left( \frac{b}{2a} \right) ^2 -\frac{c}{a} \hspace{20cm} $$
$$\Leftrightarrow \left( x + \frac{b}{2a} \right) ^2 = \frac{b^2 -4ac}{4a^2} \hspace{20cm} $$
$$\Leftrightarrow x + \frac{b}{2a} = \pm \sqrt{ \frac{b^2 -4ac}{4a^2} } \hspace{20cm} $$
$$\Leftrightarrow x = -\frac{b}{2a} \pm \frac{ \sqrt{ b^2 -4ac} }{2a} \hspace{20cm} $$
よって解の公式が得られる。\( \square \)
特にxの係数が偶数の場合
ax2+2b'x+c=0と書いて次の様な解をもつ。
$$ x = \frac{ -b' \pm \sqrt{ b'^2 - ac} }{a} \hspace{20cm} $$
重解
解の公式においてb2-4ac=0の時
x=-b/2aとなり、2次方程式の解はこれ一つである。
この場合、
二つの解が重なったものと考えて”重解”と呼ぶ。
黄金比
長方形ABCDの短辺は1、長辺はxとする。
一辺の長さ1の正方形を切り取って、
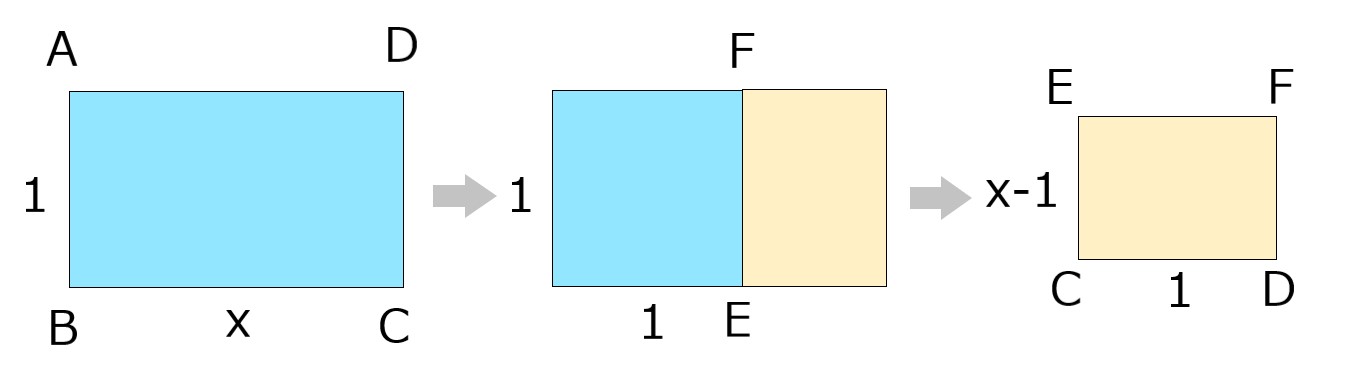
長方形ECDFを作ったら
元の長方形ABCDと相似になる様なxを求めたい。
すなわち
\( 1:x=(x-1):1 \)
が成り立っている。
これは2次方程式、
\( x(x-1)=1^2 \)
を解けば求まり
$$ x = \frac{1 +\sqrt5}{2} \hspace{20cm}$$
である。
長方形ABCDの長さの比
$$ 1 : \frac{1 +\sqrt5}{2} \hspace{20cm}$$
は”黄金比”と呼ばれている。
関数
xとyを変数とする。
xの値を定めた時、対応して
yの値がただ一つ定まるならば
yはxの”関数”である、という。
これを、
文字fなどを用い”y=f(x)”と表記し
またはyを省略して単に関数”f(x)”という。
関数の値
xをaと定めた時のyの値を”f(a)”と書き、
関数f(x)のx=aにおける”値”という。
座標平面
平面上に原点Oと、Oで垂直に交わる
x軸とy軸を定めたものを”座標平面”という。
グラフ
関数y=f(x)が与えられた時
関係y=f(x)を満たす点全体で作られる図形を
関数の”グラフ”といい、
y=f(x)を”グラフの方程式”という。
2次関数
a、b、cは定数で、a≠0とした時
関数y=ax2+bx+cをxの”2次関数”という。
放物線
2次関数のグラフは”放物線”とも呼ばれる。
平行移動
座標平面上で図形の各点を、
一定の方向に、
一定の距離だけ動かすことを”平行移動”という。



