
メネラウスの定理とチェバの定理
証明
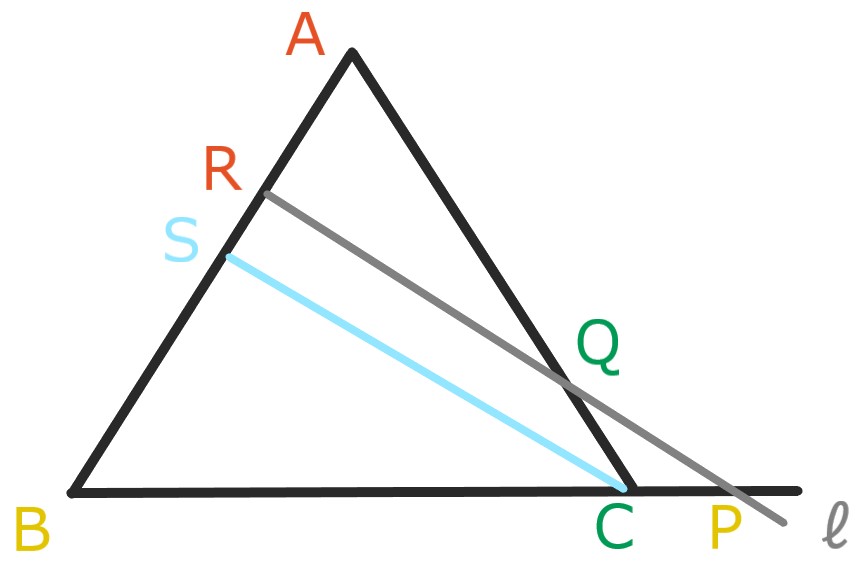
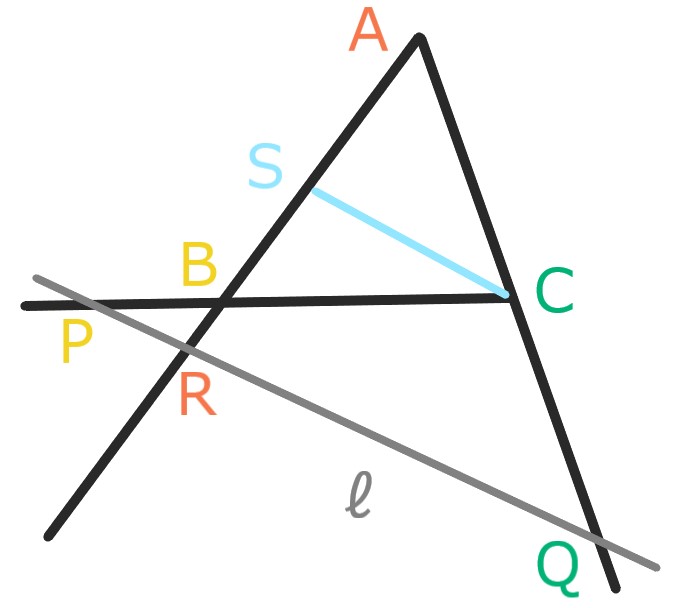
頂点Cを通りℓに平行な線を引き、
直線ABとの交点をSとする。
平行線と線分の比の関係から
$$ \frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\mathrm{BR}}{\mathrm{RS}} \hspace{20cm}$$
$$ \frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{\mathrm{SR}}{\mathrm{RA}} \hspace{20cm}$$
よって
$$ \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{BR}}{\mathrm{RS}} \cdot \frac{\mathrm{SR}}{\mathrm{RA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = 1 \quad \square \hspace{20cm}$$
証明
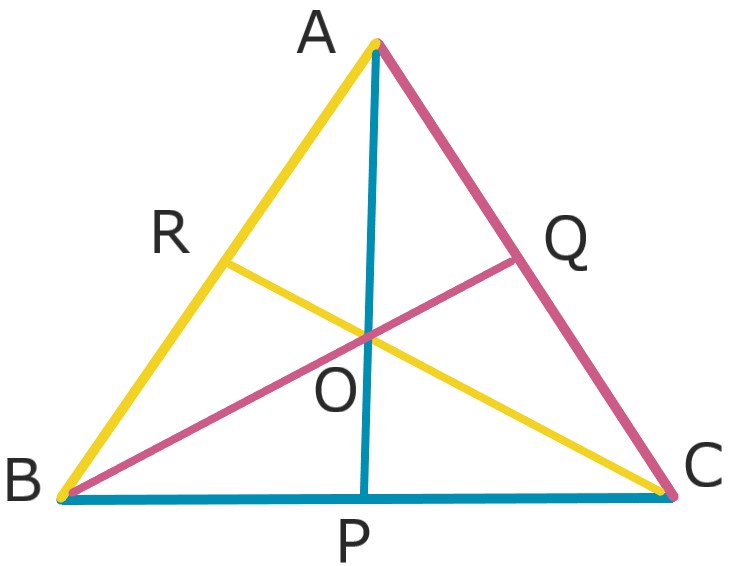
△ABPと直線CRにメネラウスの定理を使うと、
$$ \frac{\mathrm{BC}}{\mathrm{CP}} \cdot \frac{\mathrm{PO}}{\mathrm{OA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = 1 \hspace{20cm}$$
である。
同様に△APCと直線BQにも使うと、
$$ \frac{\mathrm{PB}}{\mathrm{BC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AO}}{\mathrm{OP}} = 1 \hspace{20cm}$$
上の二つの式の両辺を掛けて
$$\left( \frac{\mathrm{BC}}{\mathrm{CP}} \cdot \frac{\mathrm{PB}}{\mathrm{BC}} \right) \cdot \left(\frac{\mathrm{PO}}{\mathrm{OA}} \cdot \frac{\mathrm{AO}}{\mathrm{OP}} \right) \cdot \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} = 1 \hspace{20cm}$$
$$\Leftrightarrow \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = 1 \quad \square\hspace{20cm}$$
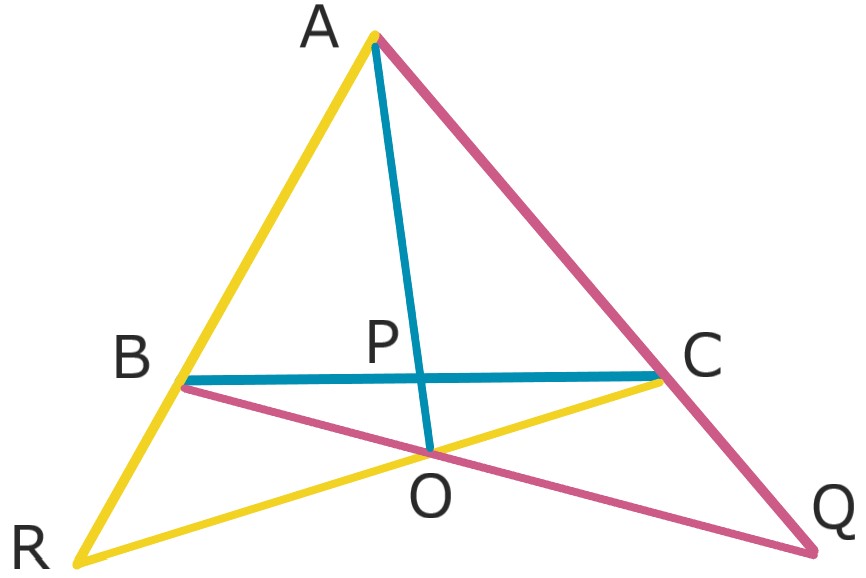
証明
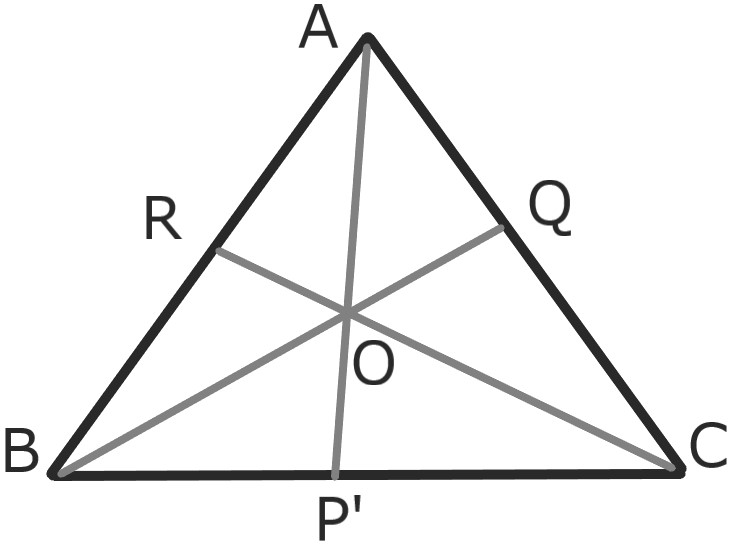
直線BQとCRの交点をOとして、
AOと辺BCの交点をP’とおく。
チェバの定理より
$$ \frac{\mathrm{BP'}}{\mathrm{P'C}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = 1 \hspace{20cm}$$
一方、仮定より
$$ \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = 1 \hspace{20cm}$$
なので
$$ \frac{\mathrm{BP'}}{\mathrm{P'C}} = \frac{\mathrm{BP}}{\mathrm{PC}} \hspace{20cm} $$
P'とPは辺BCを同じ比に内分する事がわかり、
ゆえに一致する。
3直線AP、BQ、CRは1点で交わる。\(\square\)
証明
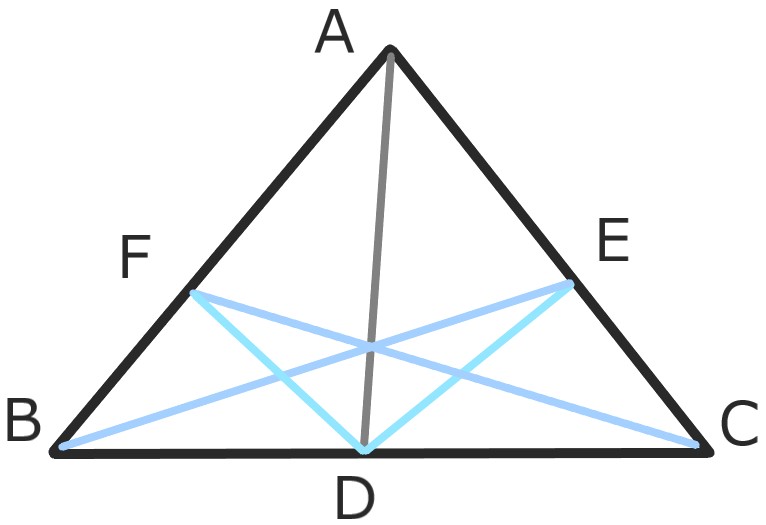
二等分線と比の関係より
$$\mathrm{BD} : \mathrm{DA} = \mathrm{BF} : \mathrm{FA} \hspace{20cm}$$
$$\mathrm{DC} : \mathrm{DA} = \mathrm{CE} : \mathrm{EA} \hspace{20cm} $$
よって
$$ \frac{\mathrm{BD}}{\mathrm{DC}} \cdot \frac{\mathrm{CE}}{\mathrm{EA}} \cdot \frac{\mathrm{AF}}{\mathrm{FB}} \hspace{20cm}$$
$$=\frac{\mathrm{BD}}{\mathrm{DC}} \cdot \frac{\mathrm{DC}}{\mathrm{DA}} \cdot \frac{\mathrm{DA}}{\mathrm{BD}} = 1 \hspace{20cm}$$
チェバの定理の逆より
3直線AD、BE、CFは1点で交わる。\(\square\)



