
リーマン積分と聞くと
難しく感じますが要は定積分のことです。
高校で習った積分には
曖昧な部分があるため、
大学数学の解析学で
厳密に定義し直したものがリーマン積分です。
長方形の面積の極限により定義される事、
リーマン積分不可能な例、
可能になる十分条件まで説明します。
リーマン積分とは
リーマン積分は高校数学で
習った定積分と同じものです。
高校の時の定義は曖昧さを含むので、
大学では厳密に定義します。
高校数学が誤魔化している事
高校数学で曖昧なのは

関数とx軸の間の面積って何?
です。
復習
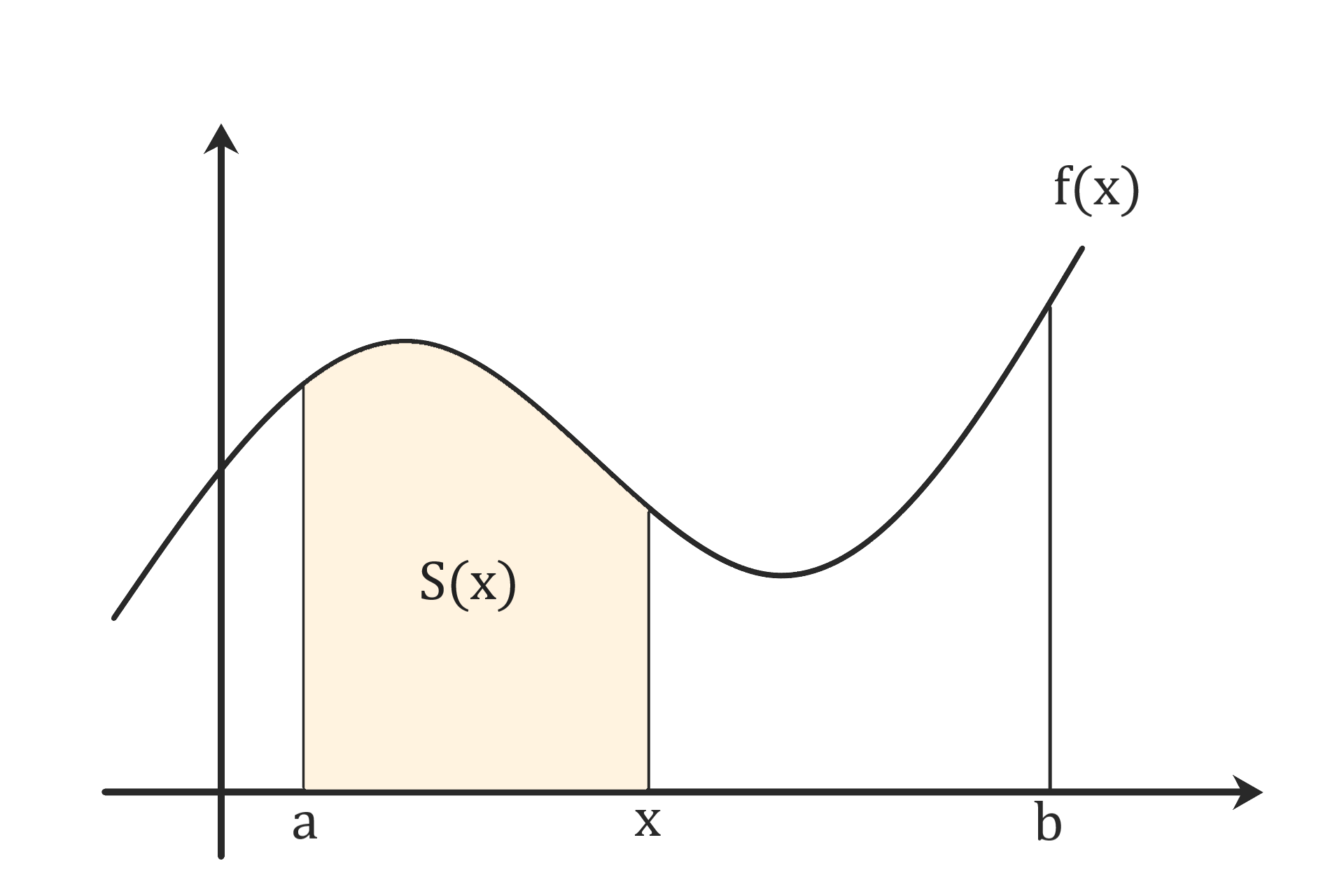
定積分の定義(高校)
関数f(x)とx軸の間の面積S(x)とすれば
\( S'(x) = f(x) \)
なのでf(x)の原始関数F(x)は
\( S(x) =F(x) -F(a) \)
を満たす。
F(b)-F(a)を記号
$$ \int_a^b f(x) dx \hspace{20cm} $$
で表しf(x)のaからbまでの定積分という。
直線で囲まれた図形の面積なら
良くわかりますが、
一般に関数は曲線を描きますし
もっと複雑な値のとり方もします。
S(x)とは何かが不明瞭なため
厳密さに欠けます。
長方形を使う
そこで長方形を用いて
関数とx軸の間の面積Sを定めます。
閉区間I=[a, b]をn+1個の点
\( a = x_0 < x_1 < x_2 < \cdots < x_{n-1} < x_n = b \)
により分割し、
各小区間を短辺に持つ長方形で
下側からと上側から関数を挟み込みます。
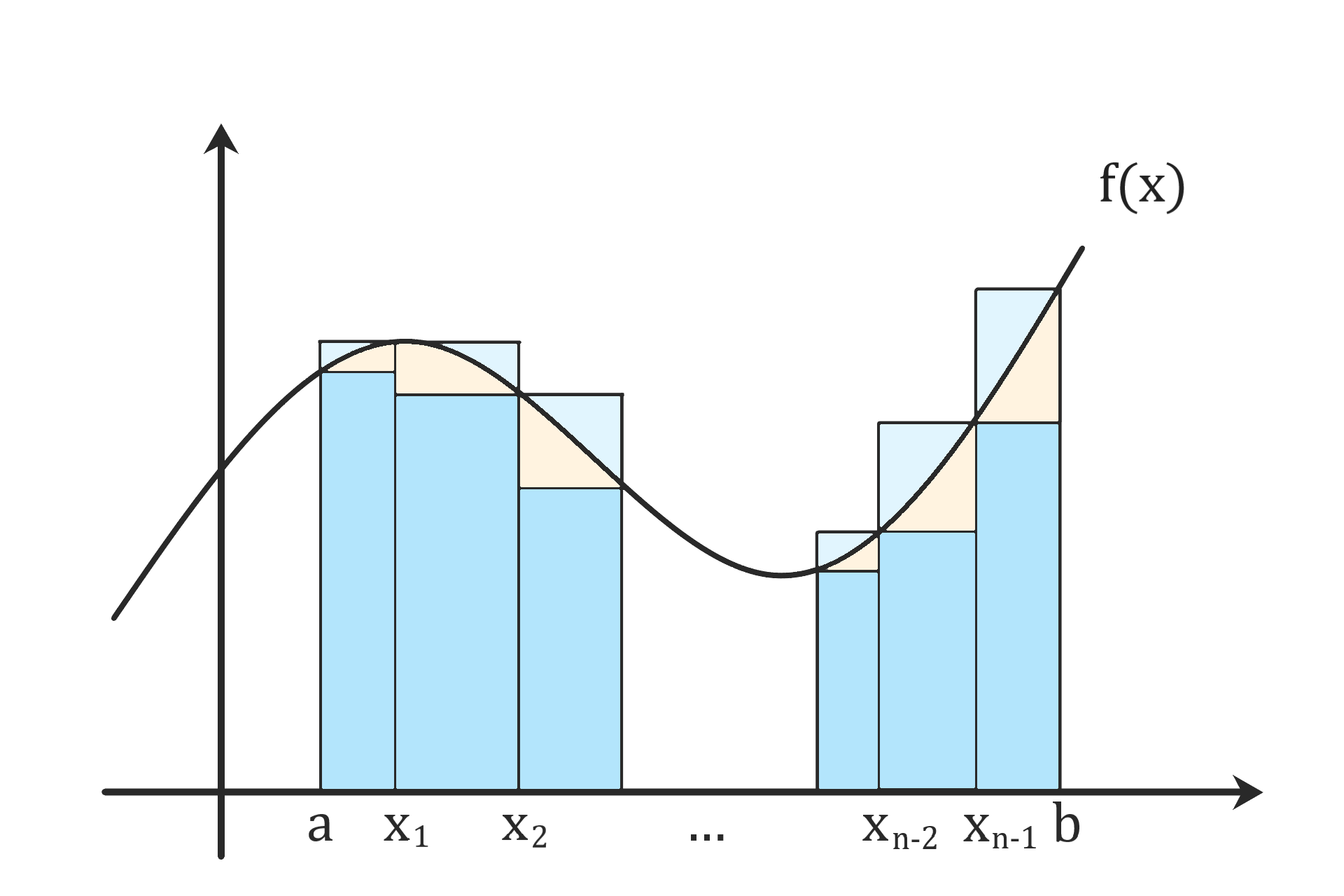
分割をΔ、
- 下側からのSの近似をsΔ
- 上側からのSの近似をSΔ
と書くなら
\( s_\Delta \leq S \leq S_\Delta \)
分割を細かくして行けば
はさみうちの原理から
Sが与えられる、と言うのが
リーマン積分の基本理念です。
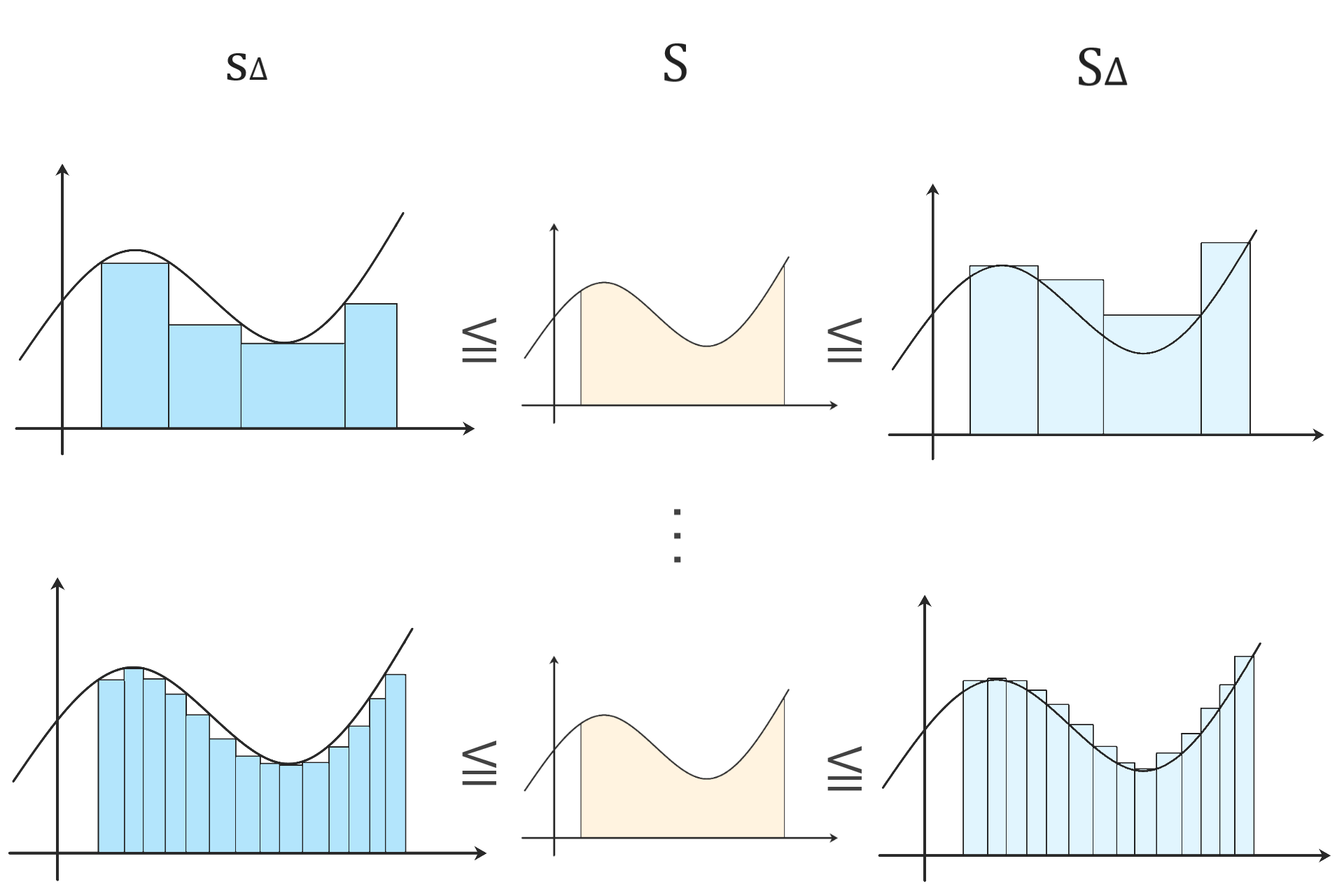
リーマン積分可能
具体的には関数が有界なら
k=1、2、…、nに対し
$$\left\{ \begin{eqnarray}m_k = \inf_{x_{k-1} \leq x \leq x_k} f(x) \\ M_k = \sup_{x_{k-1} \leq x \leq x_k} f(x)\end{eqnarray} \right. \hspace{20cm}$$
とおいて
$$\left\{ \begin{eqnarray} s_\Delta = \sum_{k=1}^n m_k (x_k -x_{k-1}) \\ S_\Delta = \sum_{k=1}^n M_k (x_k -x_{k-1}) \end{eqnarray} \right. \hspace{20cm}$$
であるよう長方形を作ります。
分割を細かくして行くと
- sΔは単調増加
- SΔは単調減少
しながらSへ近付きます。
最終的にsΔとSΔは一つの値へ
収束する事が期待されます。
すなわち
区間Iの分割すべての集合をDとして
\( \sup_{\Delta \in D} s_\Delta = \inf_{\Delta \in D} S_\Delta \)
です。
この等式が満たされた状態を
リーマン積分可能と呼びます。
リーマン積分
リーマン積分はこの
リーマン積分可能な時のみ定義されます。
定積分の定義(大学)
f(x)は閉区間Iでリーマン積分可能とする。
\( \sup_{\Delta \in D} s_\Delta \)
を
$$ \int_a^b f(x) dx \hspace{20cm}$$
で表しf(x)のIにおける定積分という。
はさみうちの原理より
関数とx軸の間の面積が
はっきり分かっているので、
今度こそ厳密に定義されました。
区分求積法
リーマン積分に似た物を高校生も習います。
それが
区分求積法
関数f(x)が区間[a, b]で連続なら
$$ \int_a^b f(x) dx = \lim_{n \to \infty} \sum_{k=1}^n \frac{b-a}{n} \times f\left(a+\frac{k(b-a)}{n} \right) \hspace{20cm}$$
です。
こちらはn+1個の点
$$ a = x_0 < a+\frac{b-a}{n} < a+\frac{2(b-a)}{n} < \hspace{20cm}$$
$$\cdots < a+\frac{(n-1)(b-a)}{n} < x_n = b $$
による分割で長方形を作ります。
リーマン積分不可能な例
リーマン積分を使えば
関数とx軸の間の面積を
必ず定められそうに思えますが、
上手く行かない事もあります。
例としてディリクレ関数を紹介します。
ディリクレ関数は
有理数全体の集合Qを用い
$$ f(x) = \left\{ \begin{eqnarray} 1 \quad (x \in \mathbb{Q}) \\ 0 \quad (x \notin \mathbb{Q}) \end{eqnarray} \right. \hspace{20cm}$$
で与えられる、実軸上
0と1を同時にとり続けている様な関数です。
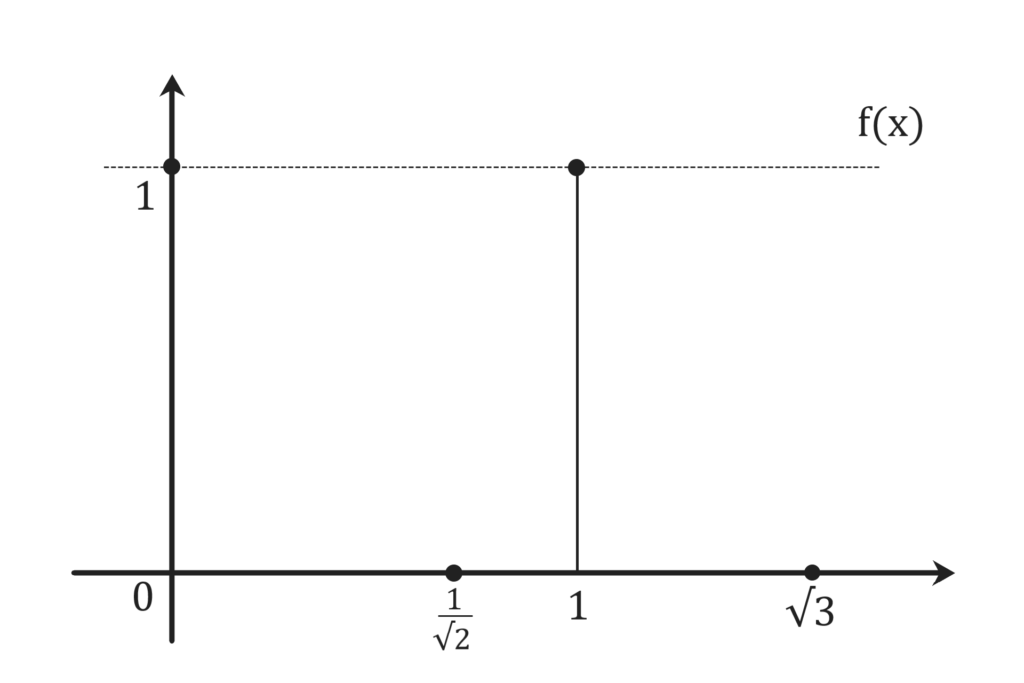
この関数の閉区間[0, 1]における
定積分を考えてみると、
任意の分割について
$$\left\{ \begin{eqnarray}0 = \inf_{x_{k-1} \leq x \leq x_k} f(x) \\ 1 = \sup_{x_{k-1} \leq x \leq x_k} f(x)\end{eqnarray} \right. \hspace{20cm}$$
なので
$$\left\{ \begin{eqnarray} 0 = \sum_{k=1}^n m_k (x_k -x_{k-1}) \\ 1 = \sum_{k=1}^n M_k (x_k -x_{k-1}) \end{eqnarray} \right. \hspace{20cm}$$
すなわち
\( 0 = \sup_{\Delta \in D} s_\Delta \neq \inf_{\Delta \in D} S_\Delta = 1 \)
となってしまい、
リーマン積分可能の等式が満たされません。
ディリクレ関数を積分できる
ルベーグ積分という理論もあります。
リーマン積分可能になる条件
リーマン積分可能を保障する
十分条件があり、
それは関数が連続な事です。
先程の例は特殊で、
多項式、sin(x)、exなど
私たちに馴染み深い関数は連続なので、
リーマン積分は大体の
関数とx軸の間の面積を測ってくれます。
多次元
n次元についても、
リーマン積分は同様に定義されます。
はさみうちの原理を基本に
関数の値を挟み込みます。
2次元すなわち
Ω=[a, b]×[c, d]上の積分とは、
\( a= x_0 < x_1 < x_2 < \cdots < x_{m-1} < x_m =b \)
\( c= y_0 < y_1 < y_2 < \cdots < y_{n-1} < y_n =d \)
によりΩを長方形
\( \Delta_{ij} = [x_{i-1}, x_i] \times [y_{j-1}, y_j] \)
に分割し
$$\left\{ \begin{eqnarray}m_{ij} = \inf_{(x, y) \in \Delta_{ij} } f(x, y) \\ M_{ij} = \sup_{(x, y) \in \Delta_{ij}} f(x,y)\end{eqnarray} \right. \hspace{20cm}$$
とおき長方形Δijの面積を|Δij|と書いて
$$\left\{ \begin{eqnarray} s_\Delta = \sum_{i=1}^m \sum_{j=1}^n m_{ij} |\Delta_{ij} | \\ S_\Delta = \sum_{i=1}^m \sum_{j=1}^n M_{ij} |\Delta_{ij} | \end{eqnarray} \right. \hspace{20cm}$$
とすればsΔとSΔは
関数の値を上下から挟めています。
Ωの分割すべての集合をDとして
\( \sup_{\Delta \in D} s_\Delta = \inf_{\Delta \in D} S_\Delta \)
が成立するなら二重積分可能と呼び、
\( \sup_{\Delta \in D} s_\Delta \)
を記号
$$ \iint_\Omega f(x, y) dx dy \hspace{20cm} $$
で表しf(x, y)のΩ上の二重積分と言います。
3次元以降も変数が増えるのみです。
まとめ
高校数学の定積分で不明瞭だった
関数とx軸の間の面積を
長方形による上下からの近似で
測ったのがリーマン積分です。
リーマン積分のおかげで
連続関数とx軸の間の面積は定義されました。
残された問題はディリクレ関数のような、
無限に多くの点で不連続な場合。
(有界かつ有限個の点のみ不連続なら実はリーマン積分可能)
ルベーグ積分へと続いて行きます。
一般にイメージされる面積は
連続な曲線で囲まれているので、
リーマン積分だけでも十分と言えば十分です。
