大学数学

多項式時間、指数時間とは？
アルゴリズムの例で説明します。

多項式時間とは計算量の内

アルゴリズム内の全処理数が
多項式回相当の物、

指数時間とは
指数関数回相当の物です。

例として

  • 最大値を求めるアルゴリズム
  • 小さい順に数を整列させるアルゴリズム

は多項式時間、

  • パスワード解読のアルゴリズム

は指数時間で計算されます。

具体的な処理数の数え方と
関連してP≠NP問題まで、

わかりやすく説明します。

多項式時間とは

10個のランダムな数字から
最大値を求めるアルゴリズムを考えます。

2、6、17、8、9、3、10、12、5、1

が入力されたとして、

この中から一番大きな数字を
コンピュータに見付けさせます。

アルゴリズムの組み方としては
左から順番に比較する方法があります。

具体的には

  • 2と6を比較、6を最大値候補として残す。
  • 6と17を比較、17を最大値候補として残す。
  • 17と8を比較、17を最大値候補として残す。
  • …
  • 17と5を比較、17を最大値候補として残す。
  • 17と1を比較、17が最大値として決定！

の様に

「２つの数字を比較して大きい方を最大値候補に残す」

という処理を９回します。

このアルゴリズムは一般に、

n個データが入力された際
n-1回の処理をします。

ポイント

n-1は多項式なので
多項式時間のアルゴリズムです。

バブルソート

今度は先ほどの10個の数字を
小さい順に並べましょう。

最大値を求めるアルゴリズムを
繰り返せば可能で、

具体的には始め

  • 2と6を比較、6を2の右側へ移動。
  • 6と17を比較、17を6の右側へ移動。
  • 17と8を比較、17を8の右側へ移動。
  • …
  • 17と5を比較、17を5の右側へ移動。
  • 17と1を比較、17を1の右側へ移動。

の様にして
最大値を数列の右端へ持って行きます。

計算前2617893101251
計算後2689310125117

続いて最大値17を除いた

2、6、8、9、3、10、12、5、1

に対し同じ事をすれば、

12が数列の右から２番目へ行きます。

今度は12を除いた

2、6、8、9、3、10、5、1

に対してと、

以下繰り返しで
次第に数列が小さい順に整列されます。

計算前2617893101251
2689310125117
2683910511217
2638951101217
…
2315689101217
2135689101217
計算完了1235689101217

n個の入力に対して

「２つの数字を比較して大きい方を右側へ移動させる」

という処理を
n-1、n-2、…、2、1回するので、

全処理数は

\(\quad (n-1)+(n-2)+ \cdots +2 +1 \)

$$= \sum_{k=1}^{n-1} k \hspace{20cm}$$

$$= \frac{1}{2}(n-1)n \hspace{20cm}$$

$$ = \frac{1}{2} n^2 -\frac{1}{2} n \hspace{20cm} $$

２次の多項式時間を持ちます。

大きい数字が登って行く様子が
泡の浮上に似ているため

このアルゴリズムは
バブルソートと呼ばれます。

オーダー記法

例えば多項式時間

\( n^3 +n^2 +n +1 \)

はn=10なら

\( \quad 10^3 +10^2 +10 +1 \)

\( = 1000 +100 + 10 +1 \)

n=100なら

\( \quad 100^3 +100^2 +100 +1 \)

\( = 1000000 +10000 +100 +1 \)

nが大きくなるにつれ、
３次の項が値を支配して行きます。

計算量の大変さは主に
最大次の項が決定し、

低次の項は無視できると考えて
この多項式時間はO(n3)と書かれます。

これをO（オーダー）記法と呼びます。

  • 最大値を求めるアルゴリズムはO(n)
  • バブルソートはO(n2)

です。

オーダー記法においては最大次の係数も省かれます。

指数時間

多項式時間で解けない問題として
暗号の解読があります。

アルファベット26文字で作られた
５桁のパスワードを一つずつ

  • aaaaa
  • aaaab
  • aaaac
  • …
  • aaaba
  • aaabb
  • …

総当たりに調べるなら、

26の５乗回のチェックで
パスワードを求められます。

n桁の場合の全処理数は26n回

指数関数で書かれるので
この計算量を指数時間と呼びます。

多項式時間に比べて
指数時間は爆発的に増えます。

P≠NP問題

アルゴリズムは改良することで
計算量を減らせます。

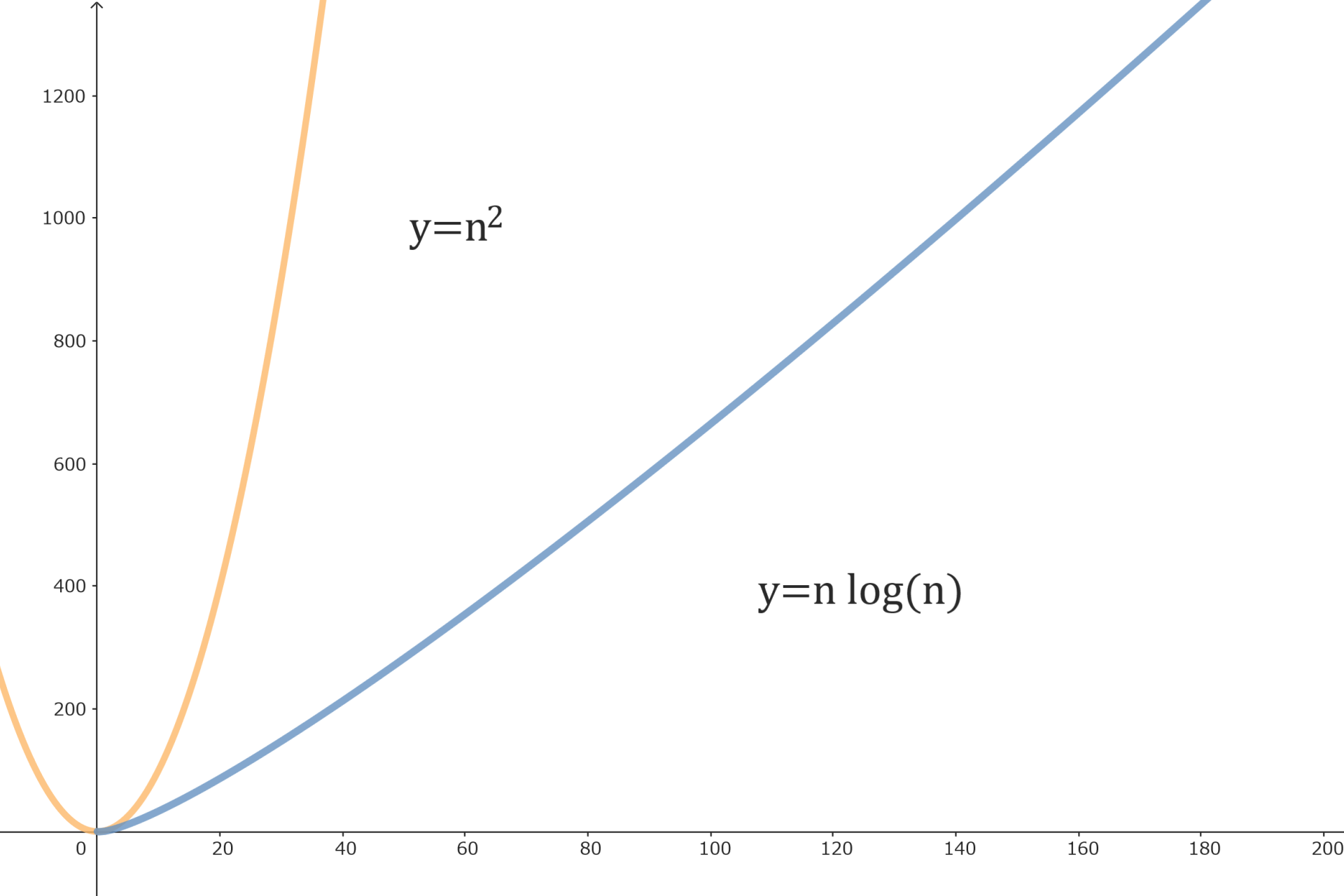
小さい順に並べるアルゴリズムも

バブルソートO(n2)の他に
クイックソートO(nlogn)が発明されており、

少なめの計算量で済みます。

計算量の比較

P≠NP問題とは

暗号解読の様な
指数時間で解かれるべき問題は

どれだけアルゴリズムを改良しても
多項式時間では解けない、という定理です。

未だ証明されておらず
世界中で研究されています。

もし指数時間の問題を
多項式時間で解けてしまうと、

パスワードを
短時間で突破されてしまうため

情報の秘密を保障する大事な定理です。

用語

  • P(polynomial time)
  • NP(nondeterministic polynomial time)

polynomial timeの日本語訳は多項式時間。

近似アルゴリズム

近似解に甘んじるなら、

指数時間の問題も
多項式時間で解けます。

最短経路を求める
巡回セールスマン問題も、

最短に近い経路は
多項式時間により求まります。

まとめ

冒頭で私は、
多項式時間とは計算量の内

アルゴリズム内の全処理数が
多項式回相当の物の様に

多項式回ではなく
多項式回相当と説明しました。

これは多項式では書かれないけど、

多項式と同じ勢いで
増えて行く関数もあるからです。

この意味を正確に理解するには
ランダウ記号の勉強が必要なため、

ここでは分かりやすさ重視で
相当という言葉を使いました。

そもそも多項式時間は
オーダー記法を前提に作られる概念で

厳密な定義の勉強には

第５章 プログラミングの基礎「計算量」

がお勧めです。

-大学数学