
sin45°、cos60°といった有名角の値は求まりますが
sin10°、cos20°などには三角関数表が必要です。
この記事では
三角関数の値の計算に使われている公式を紹介、
使い方をcos60°を例に確かめた後
エクセルに応用して
三角関数表が本当に作れる事を見たいと思います。
三角関数の公式
三角関数の値の計算には
大学で習う次の公式を用います。
sinxの公式
$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots \hspace{20cm}$$
$$\quad \; \; \! \left( =\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n+1}}{(2n+1)!} \right) \hspace{20cm}$$
cosxの公式
$$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots \hspace{20cm}$$
$$\quad \; \; \left( =\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n}}{(2n)!} \right) \hspace{20cm}$$
タンジェントはサインとコサインから求まります。
tanxの公式
$$ \tan x = \frac{\sin x}{\cos x} \hspace{20cm}$$
xにはラジアンを代入
上の公式のxにはラジアン[rad]の形で角度を代入します。
例えばcos60°を求めたい時は、
$$ 60^\circ = \frac{\pi}{3} [\mathrm{rad}] \hspace{20cm}$$
なので
$$ \cos \frac{\pi}{3} = 1-\frac{1}{2!} \cdot \left(\frac{\pi}{3}\right)^2+\frac{1}{4!}\cdot \left(\frac{\pi}{3}\right)^4-\frac{1}{6!}\cdot \left(\frac{\pi}{3}\right)^6+\cdots \hspace{20cm}$$
となります。
右辺の足し算は無限に続くので
全てを計算する事は無理です。
そこで途中までの計算結果を誤差を許容して認めます。
無限の部分を切り捨てて、
$$ \cos \frac{\pi}{3} \fallingdotseq 1-\frac{1}{2!} \cdot \left(\frac{\pi}{3}\right)^2+\frac{1}{4!}\cdot \left(\frac{\pi}{3}\right)^4-\frac{1}{6!}\cdot \left(\frac{\pi}{3}\right)^6 \hspace{20cm}$$
とし円周率3.14で計算を続けると
$$ \fallingdotseq 1-\frac{1}{2!} \cdot \left(\frac{3.14}{3}\right)^2+\frac{1}{4!}\cdot \left(\frac{3.14}{3}\right)^4-\frac{1}{6!}\cdot \left(\frac{3.14}{3}\right)^6 \hspace{20cm}$$
$$ \fallingdotseq 1-0.548+0.05-0.00183 \hspace{20cm}$$
\( = 0.50017 \)
正確な値cos60°=1/2=0.5000…と比較して
小数点以下第3位までは一致しています。
小数第3位付近までの三角関数表を作る事ができます。
足し算の量を増やすと、
小数第何位までの三角関数表も作れます。
三角関数表の作り方
ここからはエクセルを使い、
実際に三角関数表を作って行きます。
角度を入力
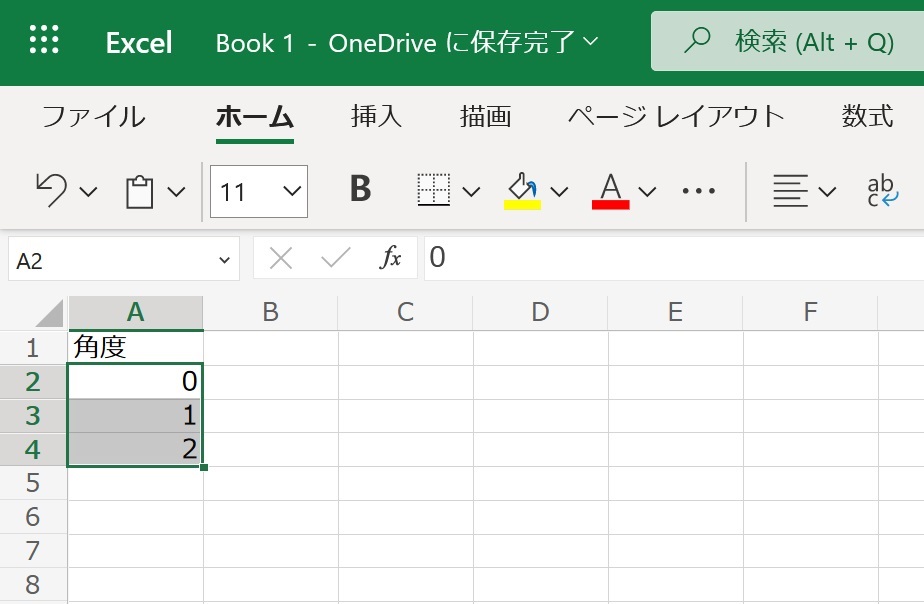
始めに0~90°まで角度を入力します。
A列に0、1、2と書き込んで、
範囲選択したら右下にカーソルを合わせ
下に向けてドラッグします。
ラジアンに変換
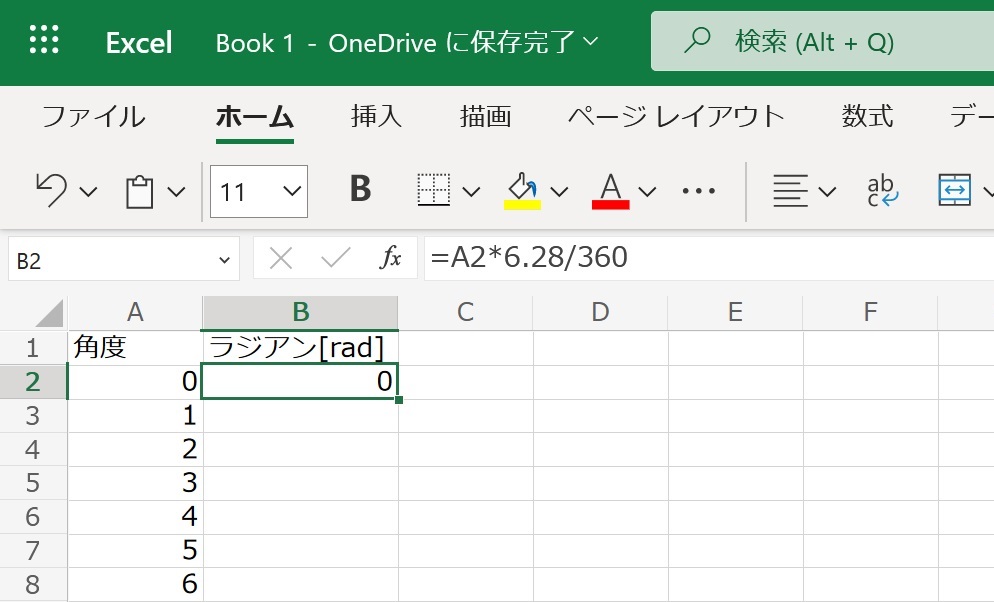
角度の入力が済んだら
度数法から弧度法に直します。
$$ 360^\circ = 2 \pi [\mathrm{rad}] \hspace{20cm}$$
の関係があるので
$$ 1^\circ = \frac{2 \pi }{360} [\mathrm{rad}] \hspace{20cm}$$
です。x°は
$$ x^\circ = \frac{2 \pi }{360}x [\mathrm{rad}] \hspace{20cm}$$
の様にラジアンへと変換されます。
円周率は3.14としてB2セルには
=A2*6.28/360と書き込みます。
同様に下までドラッグします。
sinx
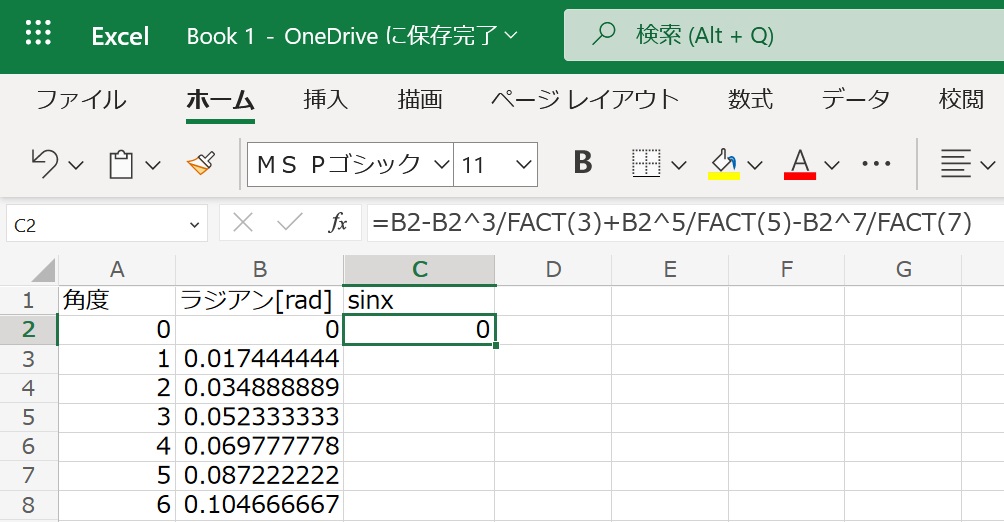
サインから順番に三角関数の値を求めます。
sinxの近似式は
$$\sin x \fallingdotseq x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!} \hspace{20cm}$$
だったのでC2セルには
=B2-B2^3/FACT(3)+B2^5/FACT(5)-B2^7/FACT(7)と書き込みます。
cosx
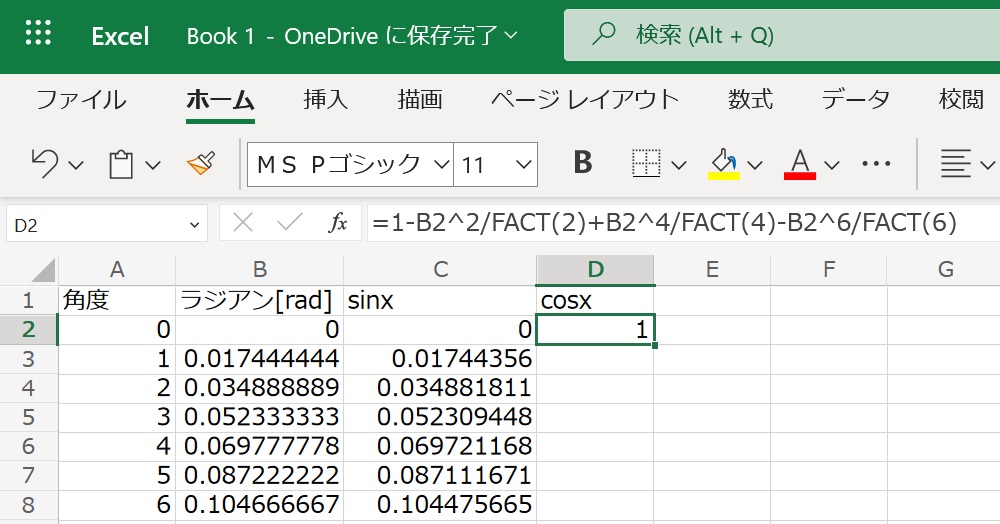
続いてcosxの近似式は
$$\cos x \fallingdotseq 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!} \hspace{20cm}$$
なのでD2セルに
=1-B2^2/FACT(2)+B2^4/FACT(4)-B2^6/FACT(6)と書き込みます。
tanx
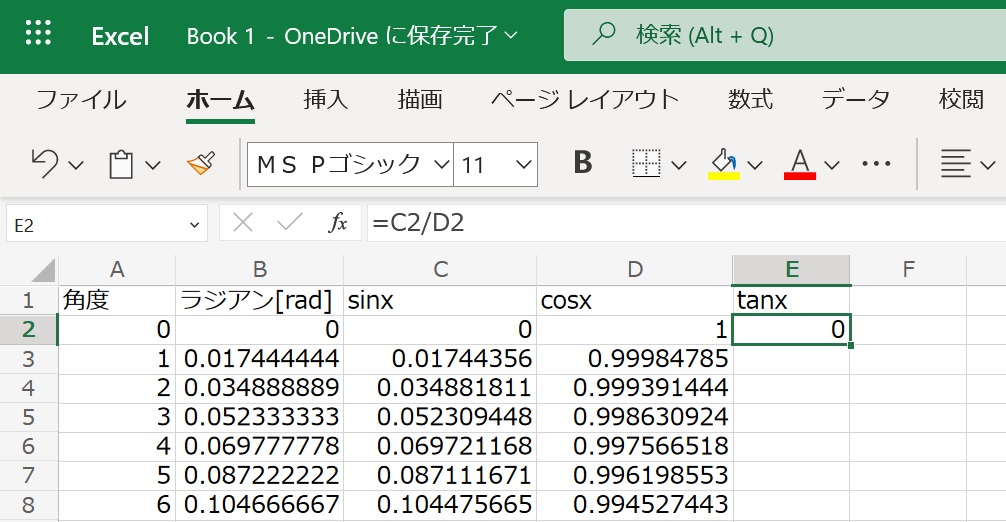
最後にタンジェントは
$$ \tan x = \frac{\sin x}{\cos x} \hspace{20cm}$$
よりE2セルに
=C2/D2と書き込んで終了です。
完成
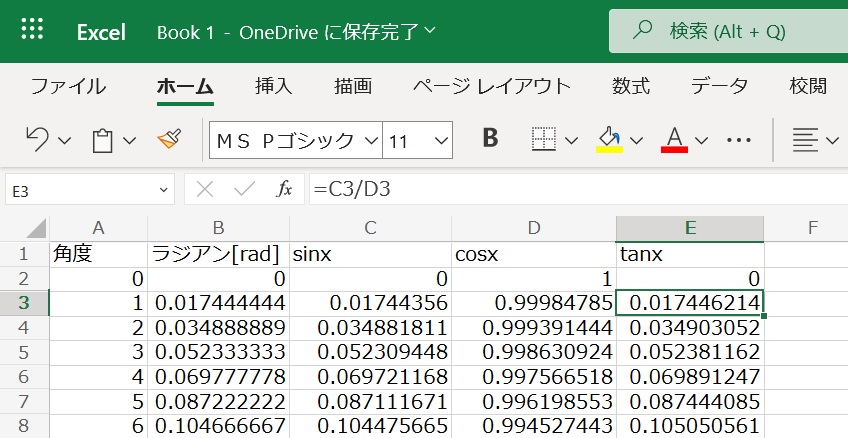
三角関数表を作れました。
色を塗ってPDFとして出力した物がこちら
まとめ
どんな角度の三角関数も求められる公式は
テイラー展開と言い、
大学の理系学部に行くと勉強できます。
最も有名な計算ソフトである
エクセルを例に、
公式の応用で
三角関数表を作れることを確かめました。
