
図形に関する問題は
xy-座標内で解く事にこだわらず、
逆を持つ写像で
別のuv-座標に移動し
図形を綺麗な形にしてからの方が
易しくなる事があります。
この際、
二つの座標の行き来に用いられる
写像を座標変換といい
有名なものは線形変換、極座標変換があります。
座標変換の定義から始めて
具体例でイメージを掴めるよう説明したいと思います。
定義
n次元における座標変換は次で定義されます。
座標変換(n次元)
写像
\( f: \mathbb{R}^n \to \mathbb{R}^n \)
が領域D⊂Rnの上で単射な時、座標変換という。
2次元の場合、写像は
\( f: \mathbb{R}^2 \to \mathbb{R}^2 \)
定義域をuv-平面
値域をxy-平面と名付けるなら
\( (x, y) = f(u, v) \)
の形でfは与えられます。
領域Dで単射より
fの定義域をDに制限した写像
\( f: D \to f(D) \)
は全単射、f(D)からDへの逆写像f-1が存在し
Dとf(D)の間をこれらの写像を通じて
行き来できる状況になっています。
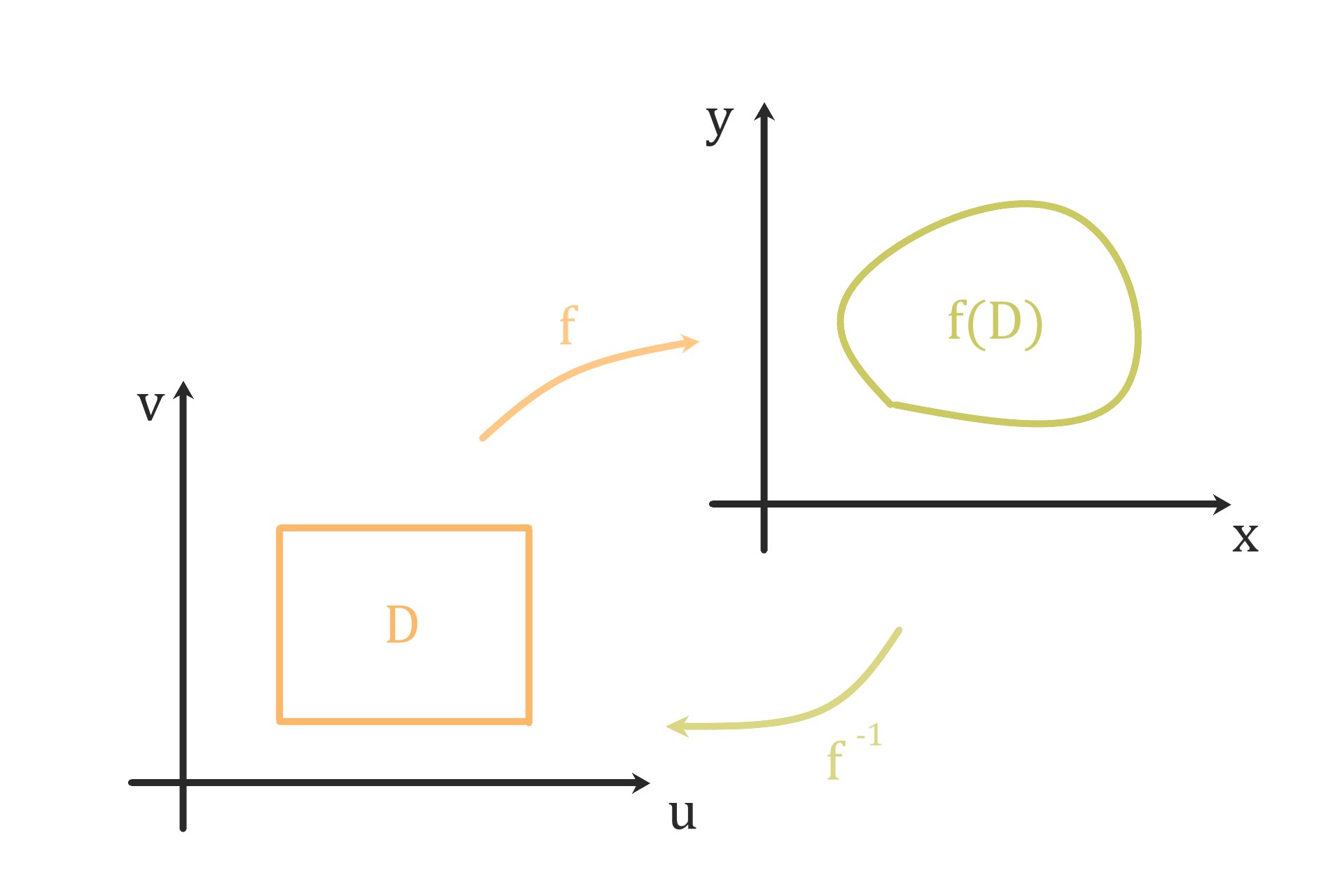
なるべく綺麗な形のD(多くは長方形)、
適切なfを用意して
f(D)と問題になっている図形を等しくします。
Dとf(D)の各点はfで対応付いているため
uv-平面で解いた結果をxy-平面に還元できます。
この定義に加えて偏微分可能性を仮定し
ヤコビアンを計算できる様にする事も多いです。
具体例
2次元の座標変換の例を紹介して行きます。
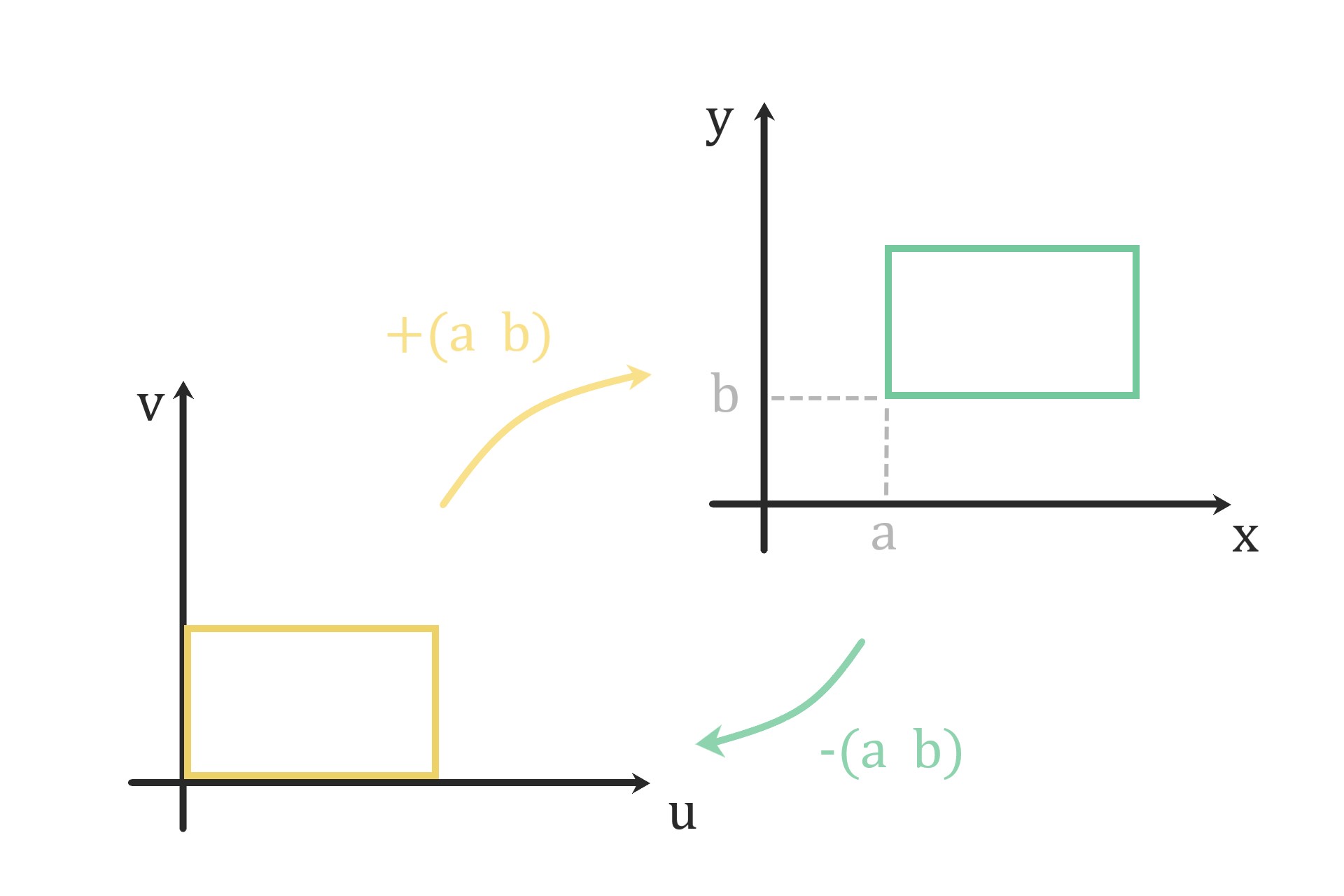
平行移動
平行移動する座標変換は次で与えられます。
$$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} u \\ v \end{bmatrix} +\begin{bmatrix} a \\ b \end{bmatrix} \hspace{20cm}$$
対象の図形を原点に持って来れます。
拡大・縮小
拡大または縮小する座標変換は次で与えられます。
$$ \begin{bmatrix} x \\ y \end{bmatrix} = \alpha \begin{bmatrix} u \\ v \end{bmatrix} \quad \left( = \begin{bmatrix} \alpha & 0 \\ 0 & \alpha \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} \right) \hspace{20cm}$$
単位幅に揃えられます。
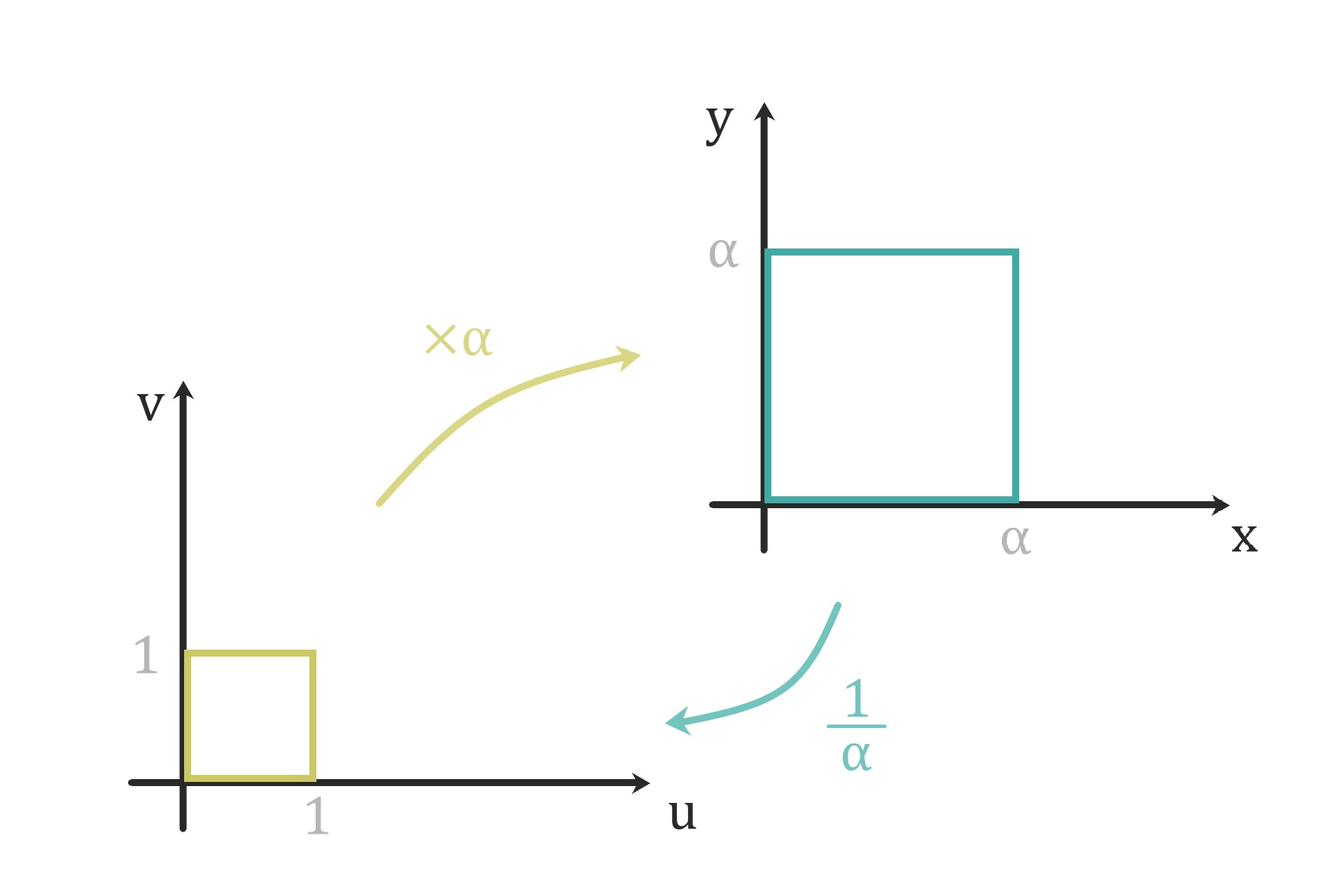
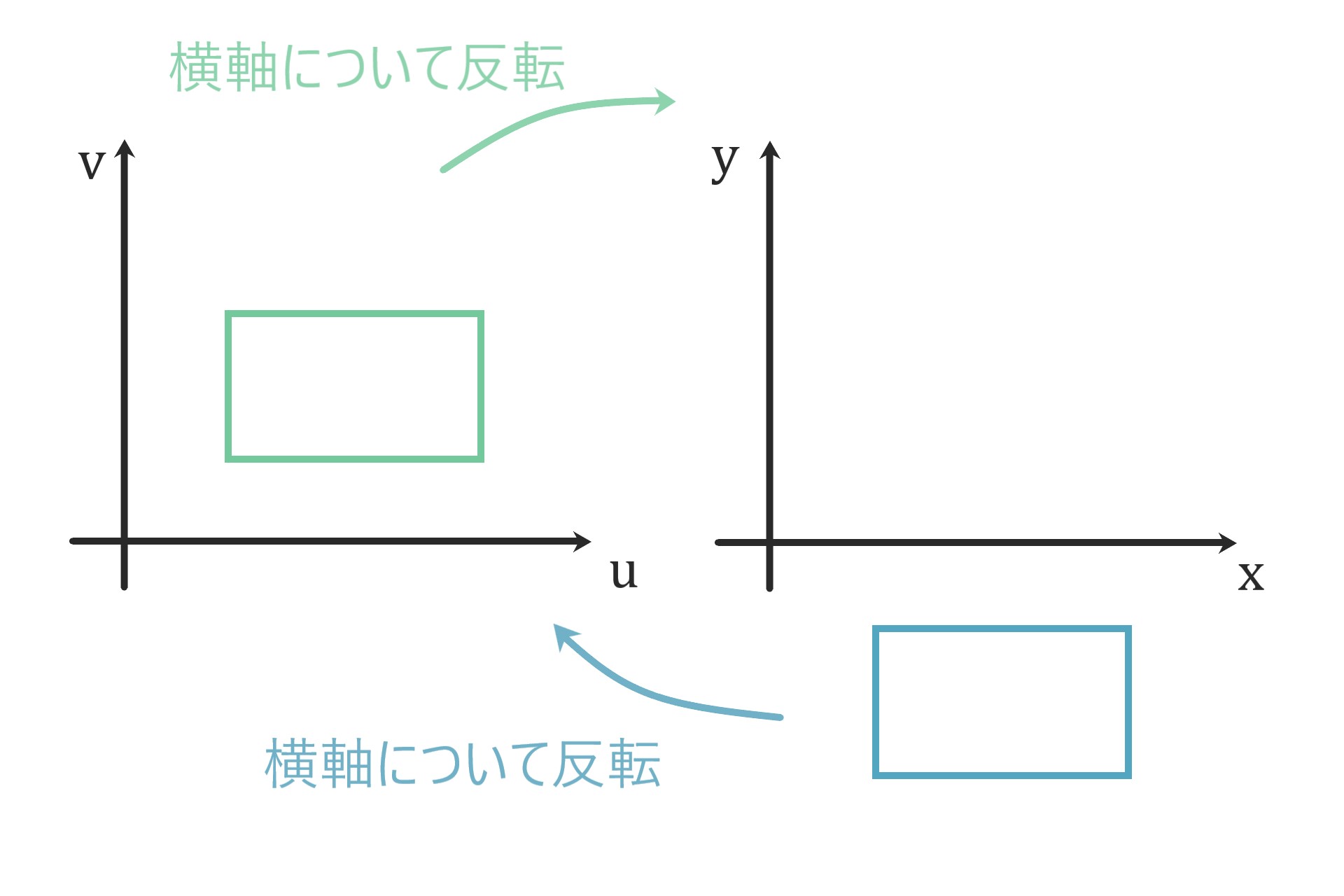
反転
横軸について鏡写しにする
座標変換は次で与えられます。
$$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} u \\ -v \end{bmatrix} \quad \left( = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} \right) \hspace{20cm}$$
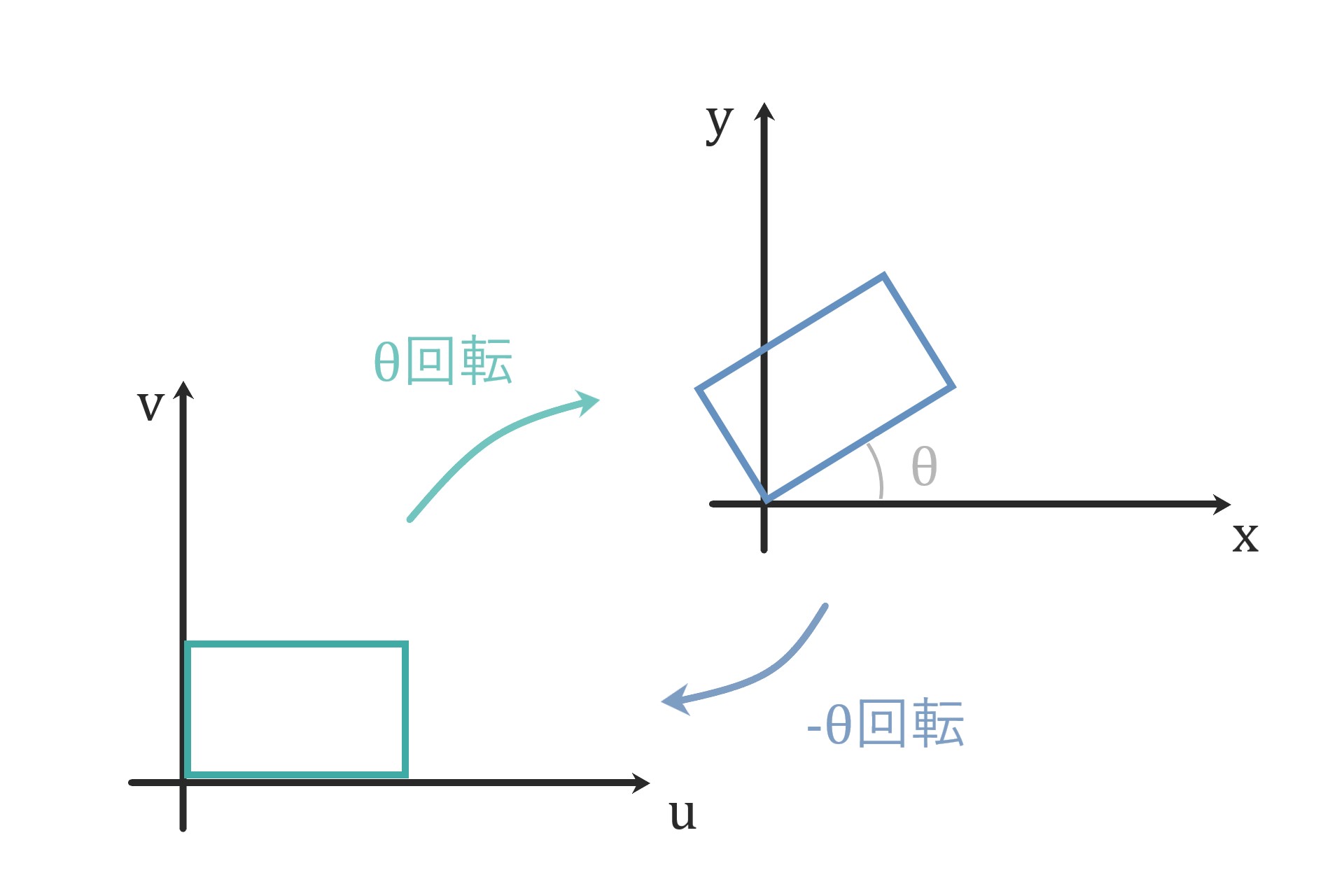
回転
反時計回りにθ回転する
座標変換は次で与えられます。
$$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix}\hspace{20cm} $$
斜めになっている図形を整えられます。
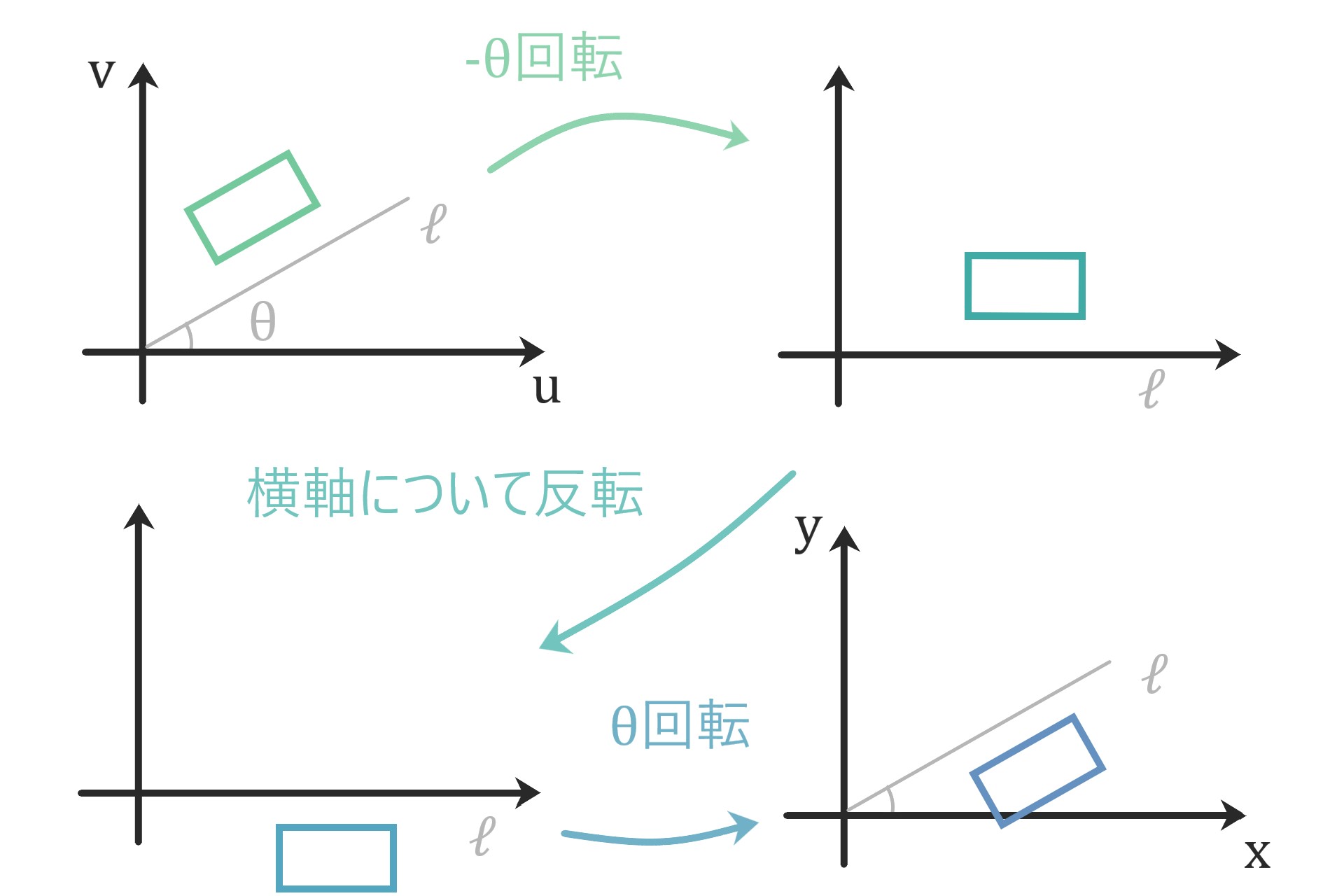
角度θの軸についての反転
角度θの直線ℓを軸にした反転は次で与えられます。
$$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} \hspace{20cm}$$
-θ回転が
$$ \begin{bmatrix} \cos (-\theta) & -\sin (-\theta) \\ \sin (-\theta) & \cos (-\theta) \end{bmatrix} = \begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} \hspace{20cm} $$
なので下図の通りに合成しています。
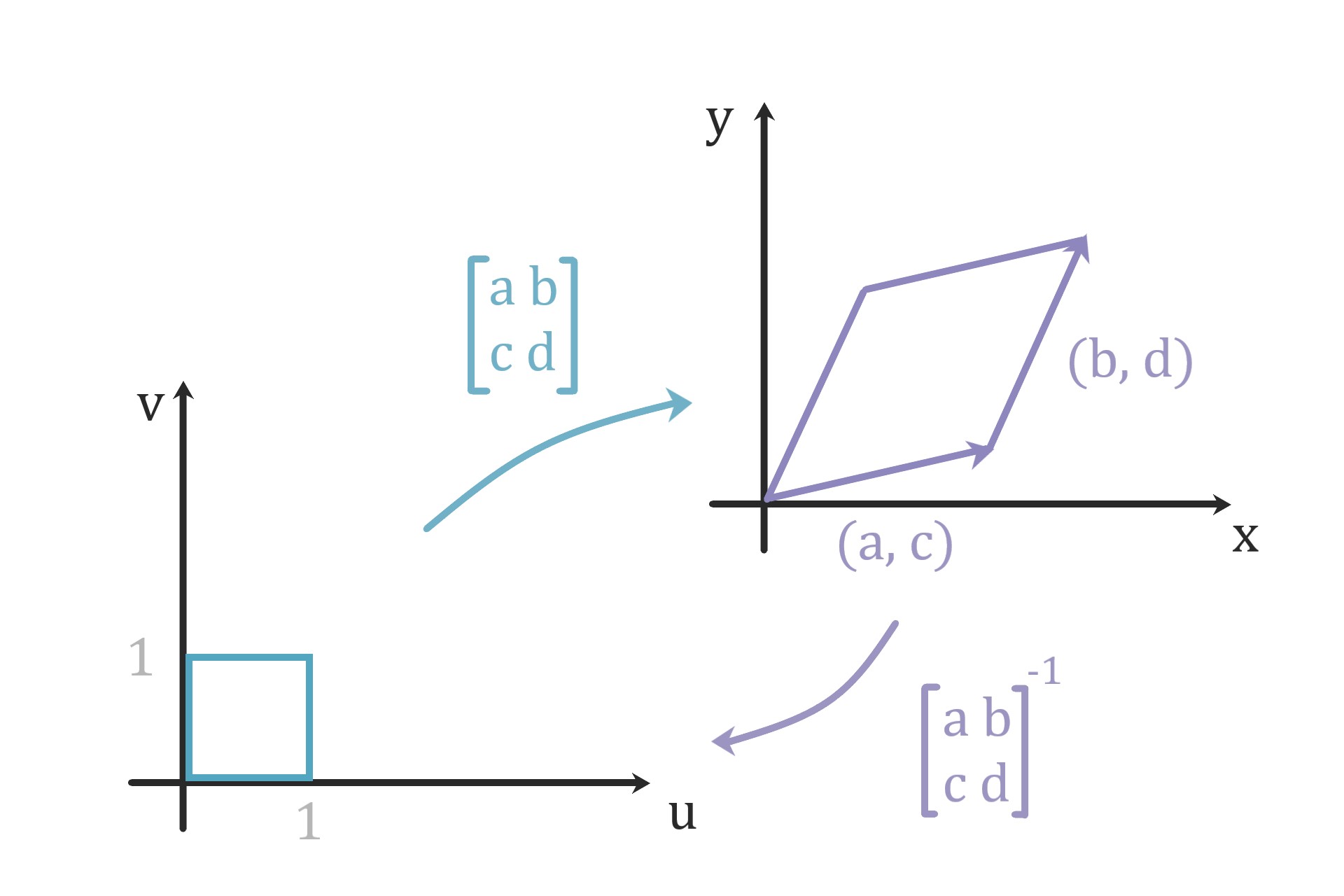
線形写像
線形写像
$$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} \hspace{20cm} $$
は行列式の値が0の時
単射であり座標変換として扱えます。
これは
$$ =\begin{bmatrix} a & b \\ c & d \end{bmatrix} \left( u \begin{bmatrix} 1 \\ 0 \end{bmatrix} +v \begin{bmatrix} 0 \\ 1 \end{bmatrix} \right) \hspace{20cm}$$
$$ = u \begin{bmatrix} a \\ c \end{bmatrix} +v \begin{bmatrix} b \\ d \end{bmatrix} \hspace{20cm}$$
の様に書けるので
$$ \begin{bmatrix} 1 \\ 0 \end{bmatrix} \quad \begin{bmatrix} 0 \\ 1 \end{bmatrix} \hspace{20cm}$$
を単位ベクトルとする座標(通常の直交座標)
において(u, v)の位置に居た点が
$$ \begin{bmatrix} a \\ c \end{bmatrix} \quad \begin{bmatrix} b \\ d \end{bmatrix} \hspace{20cm}$$
を単位ベクトルとする座標の
(u, v)の位置に移動したと理解できます。
斜交座標と同じ考え方です。
正方形
\( \{ (u, v) \, | \, 0<u<1, \, 0<v<1 \} \)
をベクトル(a, c)、(b, d)で張られる平行四辺形に写します。
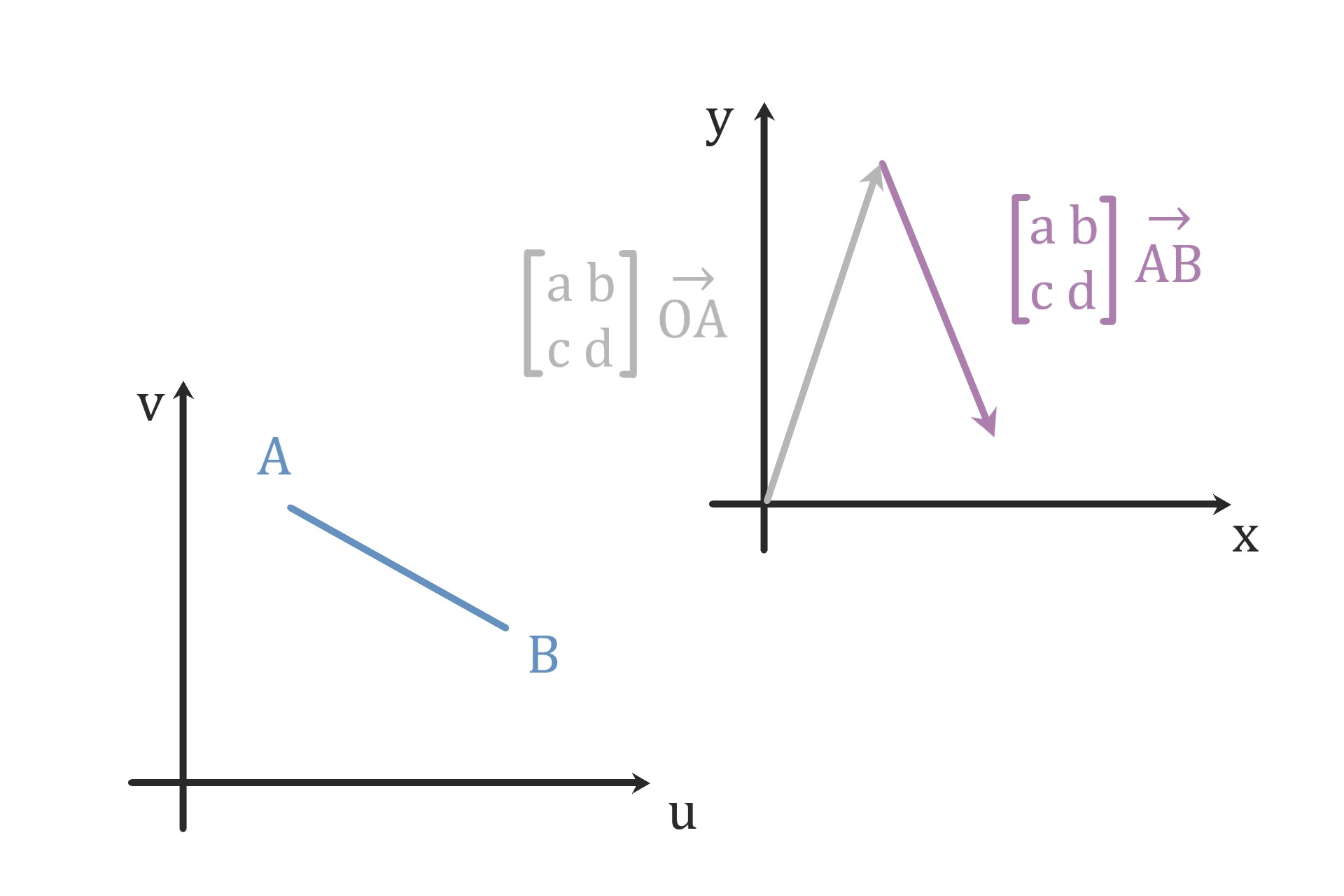
性質
線形写像で0は0に
$$ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \hspace{20cm}$$
また直線は直線に写ります。
$$ \quad \begin{bmatrix} a & b \\ c & d \end{bmatrix} \left( \overrightarrow{\mathrm{OA}} +t\overrightarrow{\mathrm{AB}} \right) \hspace{20cm}$$
$$ = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \overrightarrow{\mathrm{OA}} +t \begin{bmatrix} a & b \\ c & d \end{bmatrix} \overrightarrow{\mathrm{AB}} \hspace{20cm}$$
アフィン写像用語
ここまでの平行移動、回転などの
座標変換fはすべて
\( f(\vec{x} ) = A\vec{x} +\vec{b} \)
の形をしています。
この様な行列の掛け算または
ベクトルの足し算で表される写像を
アフィン写像と呼びます。
極座標変換
縦の長さ2πの長方形領域
\( \{ (r, \theta) \, | \, 0<r<a, \quad 0<\theta<2\pi \} \)
は極座標変換
$$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} r \cos \theta \\ r \sin \theta \end{bmatrix} \hspace{20cm}$$
により円に近い図形
\( \{ (x, y) \, | \, x^2 +y^2 <a^2\} \setminus \{ (x, 0) \, | \, 0\leq x \leq a \} \)
に写せます。

多重積分の変数変換に応用
この座標変換は円上での積分に便利です。
被積分関数を有界とすれば
境界上での積分値は0なので、
円に近い図形上の積分と
円上の積分は等しくなります。
ヤコビアンを通じて
長方形上の積分へと書き換えられ、
多重積分が容易になります。
まとめ
座標変換とは
図形についての問題を簡単にするテクニックです。
xy-座標において歪な形の図形も、
適切な単射な写像fを定めて
uv-座標で見直すと綺麗な形にできます。
その際(x, y)と(u, v)各点が
結び付いている必要があり、
紐づけを担うのがfと逆写像f-1です。
応用例としては
多重積分の変数変換で、
球上の積分には極座標変換
線形写像もヤコビアンと関連して
定理の証明に利用されます。

