【線形代数】
行列式の絶対値＝n次元平行体の体積、の証明

2023年5月9日

行列式の大きさは図形的には、

行列を構成するn個の独立なベクトルで
張られる平行体の体積を意味します。

これは

２次元では平行四辺形
３次元では平行六面体

の体積を計算するための道具となり

n次元については、

多重積分の座標変換の際
ヤコビアンが利用される理由でもあります。

この記事では、線形代数の知識を用いて
行列式の絶対値がn次元平行体の体積である事を証明します。

行列の基本変形、シュミットの正規直交化など

多次元の体積

始めに（ユークリッド距離の入った）
実空間Rⁿのk個の一次独立なベクトル

$ \{ \vec{x}_1 , \cdots , \vec{x}_k \} $

で張られるk次元の平行体

$ P = \{ t_1 \vec{x}_1 + \cdots +t_k \vec{x}_k \, | \, 0 \leq t_i \leq 1 , \; i = 1, \cdots , k \} $

の体積vol(P)を定義します。

１次元

１次元の時は

$ P = \{ t_1 \vec{x}_1 \, | \, 0 \leq t_1 \leq 1 \} $

であり、体積は長さを意味するので

１次元の体積

$ vol(P) := |\vec{x}_1| $

の様に定義されます。

k次元

k次元については補題が必要です。

補題

ベクトルx₁は二つのベクトルB、C

$ \vec{x}_1 = \vec{B} + \vec{C} $

に分解される。

ここでBとCは

$ \vec{B} \perp \vec{x}_i \quad (i = 2, \cdots , k) $

$ \vec{C} \in \left<\vec{x}_2, \cdots , \vec{x}_k \right> $

を満たす。

証明

一次独立なk-1個のベクトル

$ \{ \vec{x}_2, \cdots , \vec{x}_k \} $

にシュミットの正規直交化を施して

$ \{ \vec{a}_2, \cdots , \vec{a}_{k} \} $

を得る。

ポイント

$ \left<\vec{x}_2, \cdots , \vec{x}_k \right> = \left<\vec{a}_2, \cdots , \vec{a}_k \right> $

$$ \vec{B} := \vec{x}_1 - \sum_{i=2}^k (\vec{x}_1 \cdot \vec{a}_i)\, \vec{a}_i \hspace{20cm}$$

によりベクトルBを定めれば

$ \vec{B} \perp \vec{a}_i \quad (i = 2, \cdots , k) $

なのでx_iについても

$ \vec{B} \perp \vec{x}_i \quad (i = 2, \cdots , k) $

また、

$$ \vec{C} := \sum_{i=2}^k (\vec{x}_1 \cdot \vec{a}_i)\, \vec{a}_i \hspace{20cm}$$

によりベクトルCを定めればCは
{a₂, ..., a_k}で生成されるベクトル空間の元。

$ \vec{C} \in \left<\vec{a}_2, \cdots , \vec{a}_k \right> $

であり

$ \vec{C} \in \left<\vec{x}_2, \cdots , \vec{x}_k \right> $

ベクトルBとCの和は

$ \vec{x}_1 = \vec{B} + \vec{C} \quad \square$

体積の定義

$ P = \{ t_1 \vec{x}_1 + \cdots +t_k \vec{x}_k \, | \, 0 \leq t_i \leq 1 , \; i = 1, \cdots , k \} $

の体積を補題とk-1次元の平行体

$ P' = \{ t_2 \vec{x}_2 + \cdots +t_k \vec{x}_k \, | \, 0 \leq t_i \leq 1 , \; i = 2, \cdots , k \} $

の体積で定義します。

k次元の体積

$ vol(P) := |\vec{B}| \times vol(P') $

次元を落として行くと
最終的には1次元にたどり着くので、

帰納的にk次元まで定義できた事になります。

定義の意味

３つの一次独立なベクトルで張られる平行体を例に、
定義の意味を解説したいと思います。

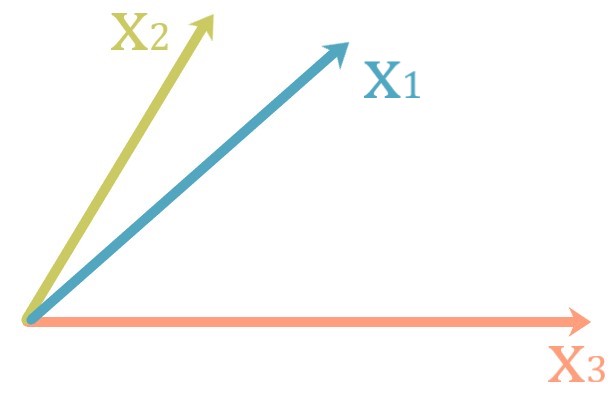
まず、次元を落として行くとx₃のみが残るので

この時点での体積は長さの|x₃|です。

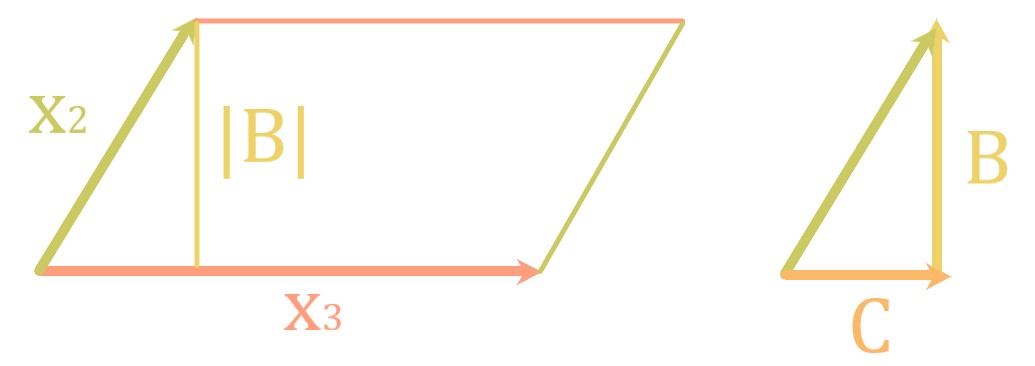
次にx₂を、x₃と平行なベクトルCと直交するベクトルBに分解して

先程の体積|x₃|に|B|を掛けます。

平行四辺形の面積を底辺×高さで求める事に対応します。

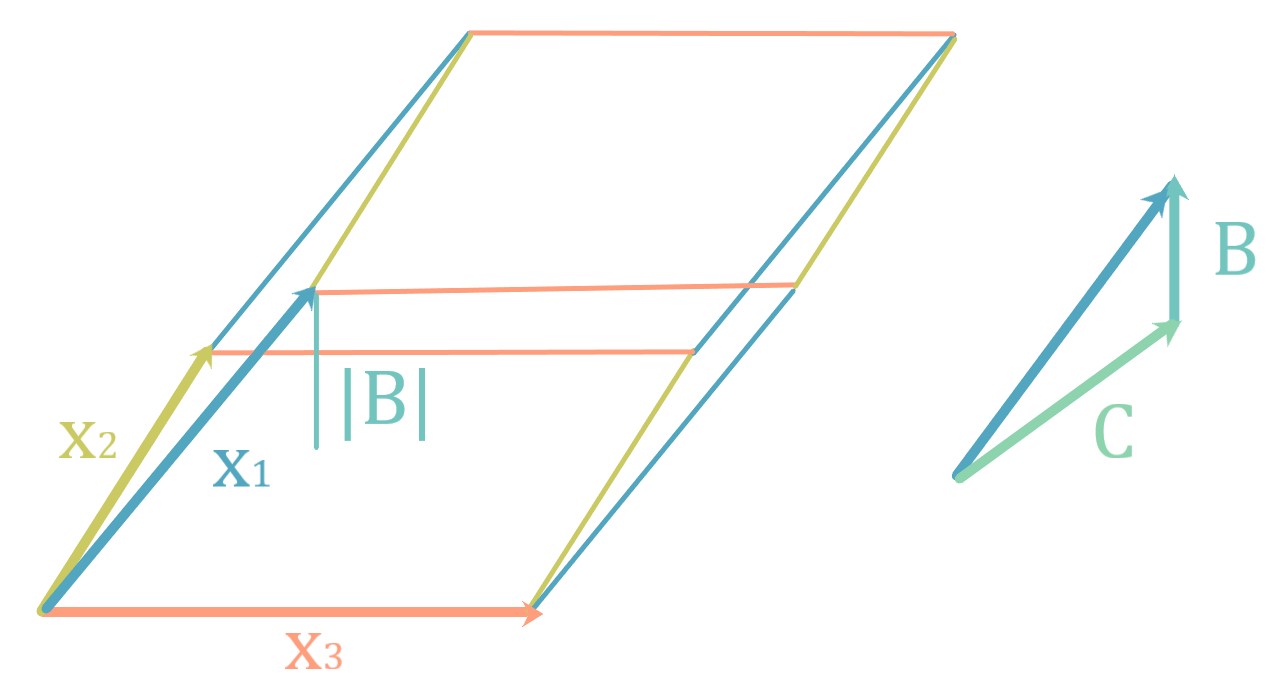
続いてx₁を、x₂とx₃で張られる平面上の
ベクトルCと直交するベクトルBに分解して

先程の体積（面積）に|B|を掛けます。

平行六面体の体積を底面積×高さで求める事に対応します。

４次元以降の体積を求めたい時は

同様に、それまでの、どのベクトルとも直交する
ベクトルBの大きさを体積に掛ける操作を繰り返します。

行列式の幾何学的意味

体積の定義が済んだので定理を証明します。

定理

実空間Rⁿのk個の一次独立なベクトル

$ \{ \vec{x}_1 , \cdots , \vec{x}_k \} $

で張られるk次元の平行体

$ P = \{ t_1 \vec{x}_1 + \cdots +t_k \vec{x}_k \, | \, 0 \leq t_i \leq 1 , \; i = 1, \cdots , k \} $

の体積vol(P)は、k×n行列A

$$ A:= \begin{pmatrix}\vec{x}_1 \\ \vec{x}_2 \\ \vdots \\ \vec{x}_k \end{pmatrix} \hspace{20cm}$$

とその転置A^Tを用いて

$ vol(P)^2 = det(A A^\top) $

の様に書かれる。

これは特にk=nの時

$ vol(P) = |det(A)| $

である。

証明

帰納法で示す。

k=1の時は

$ det(A A^\top) = det(\vec{x}_1 \vec{x}_1^\top ) = |\vec{x}_1|^2 = vol(P)^2 $

なので成立。

k-1次元の平行体に対して定理を認め、
k次元について考える。

補題を用いて

$ \vec{x}_1 = \vec{B} +\vec{C} $

と分解しAの一行目をBに換えた行列を

$$ \tilde{A}:= \begin{pmatrix}\vec{B} \\ \vec{x}_2 \\ \vdots \\ \vec{x}_k \end{pmatrix} \hspace{20cm}$$

と書く事にする。

$ \vec{C} \in \left<\vec{x}_2, \cdots , \vec{x}_k \right> $

より適当なα₂、…、α_kをとり

$ \vec{C} = \alpha_2 \vec{x}_2 +\cdots +\alpha_k \vec{x}_k $

ここで一行目にm行目のα_m倍を加える基本行列E_mを用意する。

例えばE₂、E_kは

$$ E_2 := \begin{pmatrix} 1 & \alpha_2 & \cdots & 0 \\ 0 & 1 & \cdots & 0\\ \vdots & & \ddots & \vdots \\ 0 & \cdots & 0 & 1 \end{pmatrix} \hspace{20cm}$$

$$ E_k := \begin{pmatrix} 1 & 0 & \cdots & \alpha_k \\ 0 & 1 & \cdots & 0\\ \vdots & & \ddots & \vdots \\ 0 & \cdots & 0 & 1 \end{pmatrix} \hspace{20cm}$$

である。

左側から、これらの行列を掛ければ

$ E_2 \cdots E_k \tilde{A}=A $

また両辺の転置をとり

$ A^\top = \tilde{A}^\top E_k^\top \cdots E_2^\top $

定理の右辺は

$ det(A A^\top) =det( E_2 \cdots E_k \tilde{A} \tilde{A}^\top E_k^\top \cdots E_2^\top )$

$\quad\quad\quad\quad\;\; =det( E_2 \cdots E_k) \cdot det( \tilde{A} \tilde{A}^\top) \cdot det( E_k^\top \cdots E_2^\top )$

$\quad\quad\quad\quad\;\;= 1 \cdot det( \tilde{A} \tilde{A}^\top) \cdot 1 $

$ \quad\quad\quad\quad\;\;= det( \tilde{A} \tilde{A}^\top) $

の様に書き換えられる。

次にAから一行目を取り除いた行列を

$$ D:= \begin{pmatrix} \vec{x}_2 \\ \vdots \\ \vec{x}_k \end{pmatrix} \hspace{20cm}$$

と書いて計算を続ける。

$$ \tilde{A} \tilde{A}^\top = \begin{pmatrix} \vec{B} \\ D \end{pmatrix} \begin{pmatrix} \vec{B}^\top & D^\top \end{pmatrix} = \begin{pmatrix} \vec{B}\vec{B}^\top & \vec{B}D^\top \\ D\vec{B}^\top & DD^\top \end{pmatrix} \hspace{20cm}$$

ベクトルBは

$ \vec{B} \perp \vec{x}_i \quad (i = 2, \cdots , k) $

を満たすので

$$= \begin{pmatrix} \vec{B}\vec{B}^\top & 0 \\ 0& DD^\top \end{pmatrix} \hspace{20cm} $$

行列式は

$ det(\tilde{A} \tilde{A}^\top ) = det( \vec{B}\vec{B}^\top )\cdot det( DD^\top ) $

となる。

帰納法の仮定により

$ = |\vec{B}|^2 \cdot vol(P')^2 = vol(P)^2 $

以上で

$ vol(P)^2 = det(A A^\top) $

が示された。

特にk=nの時、Aは正方行列なので

$ vol(P)^2 = det(A) \cdot det( A^\top) $

転置の行列式の値は等しく

$ = \{det(A)\}^2 $

体積は定義より０以上で

$ vol(P) = |det(A)| $

が求まる。$\square$

掛ける順の任意性（補足）

行列式の値は行を入れ換えても
符号が変わるだけです。

定義においてはx_kを起点に、

順次x_k-1、x_k-2、…、x₁まで掛けて
体積を定めましたが

定理より実は、どのベクトルを起点に
どの様な順で掛けても同じ体積になります。

直方体で言うと

縦×横×高さ
高さ×横×縦

いずれも体積が求まる事に対応します。

参考文献

論文

The Determinant: a Means to Calculate Volume

線形代数

リンク

-大学数学

大学数学

2024/4/16

底aの指数関数の値の計算方法を解説します。

実用上とても大切な底aの指数関数の値の計算方法を解説します。公式底aの指数関数の値は公式 $$ a^x = e^{x \ln a} = \exp [x \ln a ] \hspace{20cm}$$ a>0, x∈R により計算されます。 ln(a)と底eの指数関数の値はテイラー展開による近似で求まるため、右辺を計算してaxの値を得ます。詳しい解説上式は指数関数の底の変換公式を利用しています。指数関数の底の変換公式 $$ a^x = b^{\log_b a^x } = b^{x \log ...

大学数学

2024/3/12

【空気中を伝搬する音の減衰】
空気吸収の式を解説します。

空気中を伝搬する音の減衰する理由は主に音の範囲が広がることによるエネルギーの分散と空気吸収の２つです。このうち空気吸収の計算方法はISO9613-1（1993年）から規格が出ていて日本だとJIS Z8738（1999年）に載っています。またJISの原案作成に携わった吉久光一先生のこちらのPDFも勉強になります。この記事ではそれらの要点を抜き出してわかりやすく解説したいと思います。空気吸収の式音圧による理解音の減衰は指数関数的であり平面音波が空気中を進んで減衰した後の音圧は減衰係数と呼 ...

中学/高校数学大学数学

2024/2/24

【高校数学】証明の用語辞典（例文付き）

ゆえに、明らかに、など証明独自の用語の意味を数学科卒業生の私がまとめました。適宜例文を添えてわかりやすさを意識してます、証明の勉強にご利用ください。 ↓目次から読みたい所にジャンプできます。基本用語証明正しさを示すこと。定義数学的対象の説明文。二等辺三角形の定義は「三辺の内の二辺が等しい三角形」である。定理仮定のもと結論が証明されているもの。仮定問題の設定。結論証明したい事。直角三角形である事を仮定すれば結論a2+b2=c2が証明される、これを三平方の定理と呼ぶ。公理定 ...

大学数学

2023/11/21

【√２、√３が求まる】
√自然数を極限に持つ漸化式の作り方

√自然数の形の無理数を極限に持つ漸化式を紹介します。とりわけ√２を求めるのに優秀なアルゴリズムで、 √３なども指数関数の速さで計算できます。式自体は簡単でプログラムを組みやすいのでコンピュータで無理数を数値計算してみたい人の入門にお勧めです。漸化式２以上の自然数aについて定理漸化式 $$ a_{n+1}= \frac{1}{a_n} +\frac{(a-1)a_n}{a} \hspace{20cm} $$ は√aを極限に持つ。ただし初項a1は任意の正の実数。（できるだけ√aの近くにとる） ...

大学数学解析学

2023/10/2

【リーマン積分とは定積分】
リーマン積分をわかりやすく説明。

リーマン積分と聞くと難しく感じますが要は定積分のことです。高校で習った積分には曖昧な部分があるため、大学数学の解析学で厳密に定義し直したものがリーマン積分です。長方形の面積の極限により定義される事、リーマン積分不可能な例、可能になる十分条件まで説明します。リーマン積分とはリーマン積分は高校数学で習った定積分と同じものです。高校の時の定義は曖昧さを含むので、大学では厳密に定義します。高校数学が誤魔化している事高校数学で曖昧なのはです。復習定積分の定義（高校）関数f(x)とx軸の間 ...

大学数学

2023/9/24

多項式時間、指数時間とは？
アルゴリズムの例で説明します。

多項式時間とは計算量の内アルゴリズム内の全処理数が多項式回相当の物、指数時間とは指数関数回相当の物です。例として最大値を求めるアルゴリズム小さい順に数を整列させるアルゴリズムは多項式時間、パスワード解読のアルゴリズムは指数時間で計算されます。具体的な処理数の数え方と関連してP≠NP問題まで、わかりやすく説明します。多項式時間とは 10個のランダムな数字から最大値を求めるアルゴリズムを考えます。 2、6、17、8、9、3、10、12、5、1 が入力されたとして、この中から一番大きな数 ...

【ベース指弾き】
縦振動、横振動とは？画像付きで解説

【エレキベース】
ノイズの原因22個と対処法まとめ

【線形代数】
行列式の絶対値＝n次元平行体の体積、の証明

多次元の体積

１次元