【高校数学】
確率変数の定義をわかりやすく説明

確率変数とは世の中の事象と数学とを
結び付ける仕組みのことで、

厳密な定義は測度論を用いて為されます。

測度論は大学数学の範疇で
かなり難しいこと。

また一般の人は
実用に耐え得る知識があれば良くて、

厳密さはあまり求めてないと思います。

なので、ここでは

高校数学レベルの確率変数の定義を
説明したいと思います。

確率変数の定義

確率変数の定義は、

「コイン投げやサイコロ振り等」

起きる事象が有限個の離散変数と

「０～１までのランダムな小数をとる、など」

起きる事象が無限個の連続変数の二つに分かれます。

最初に離散の確率変数の定義を述べて

必要な道具を揃えてから
連続の場合に進みたいと思います。

コイン投げの例で言うと

• 表が出たらXの値は１
• 裏が出たらXの値は０

にしましょう、と取り決めて

それぞれの確率は1/2で定まっているので

この時Xは確率変数となります。

$$ \left\{ \begin{eqnarray} 1/2 \quad (X=1) \\ 1/2 \quad (X=0) \end{eqnarray} \right. \hspace{20cm}$$

なぜ、こんな変数を用意するかと言うと
事象を数学で扱える形にしたいからです。

一般的に世の中の事象は

など、数とは無関係に存在しているので

数学で取り扱うためには
数字を与える必要があります。

確率変数のおかげで今

「コインで表が出たら１、裏が出たら０」

の様に数を通して事象を考えられます。

確率変数のとる値は自由に決められる

先程の例において

• 表が出たら１
• 裏が出たら-1

としても確率変数です。

$$ \left\{ \begin{eqnarray} &1/2& \quad (X=1) \\ &1/2& \quad (X=-1) \end{eqnarray} \right. \hspace{20cm}$$

• 表が出たら１
• 裏が出たら２

でも良いですし

$$ \left\{ \begin{eqnarray} 1/2 \quad (X=1) \\ 1/2 \quad (X=2) \end{eqnarray} \right. \hspace{20cm}$$

• 表が出たら100
• 裏が出たら１

も

$$ \left\{ \begin{eqnarray} &1/2& \quad (X=100) \\ &1/2& \quad (X=1) \end{eqnarray} \right. \hspace{20cm}$$

すべて確率変数です。

確率さえ正しく定まっていれば
数の割り当て方は自由です。

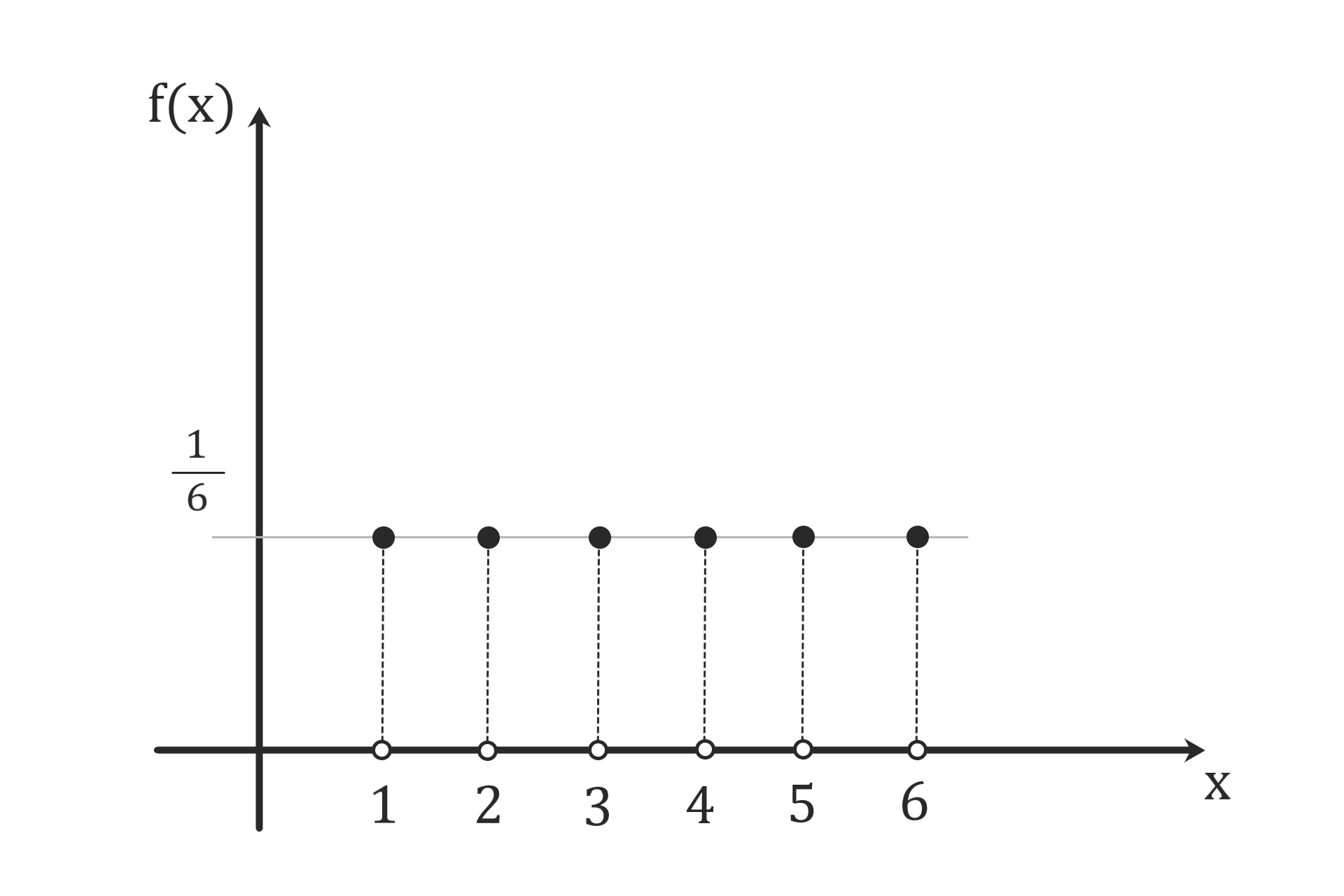
サイコロ振り

確率の問題によく登場するサイコロ振りも

• サイコロを振って１の目が出たらX=1
• サイコロを振って２の目が出たらX=2
• …
• サイコロを振って６の目が出たらX=6

として

それぞれの確率は1/6で
定まっているので確率変数になります。

確率	1/6	1/6	1/6	1/6	1/6	1/6
確率変数X	1	2	3	4	5	6

確率の記法

確率変数が値x_iをとる時の確率p_iを

\( p_i = P(X=x_i ) \)

の様に書きます。

サイコロ振りなら

• P(X=1)=1/6
• P(X=4)=1/6

です。

範囲を指定して書くことも
できて例えば

P(1≦X≦4)=4/6=2/3

です。

1≦X≦4となるのはサイコロを振って
１、２、３、４の目が出た時。

確率密度関数

離散変数について関数

$$ f(x) = \left\{ \begin{eqnarray} &p_i& \quad (x=x_i) \\ &0& \quad (x \neq x_i, \; i=1, 2, \cdots, n) \end{eqnarray} \right. \hspace{20cm} $$

は確率変数のとる値の所で
その事象の確率を示します。

この様に事象の起きる確率を表す関数を

確率密度（または確率密度関数）と呼びます。

連続変数

確率密度関数を用いて
連続の場合の確率変数を定義します。

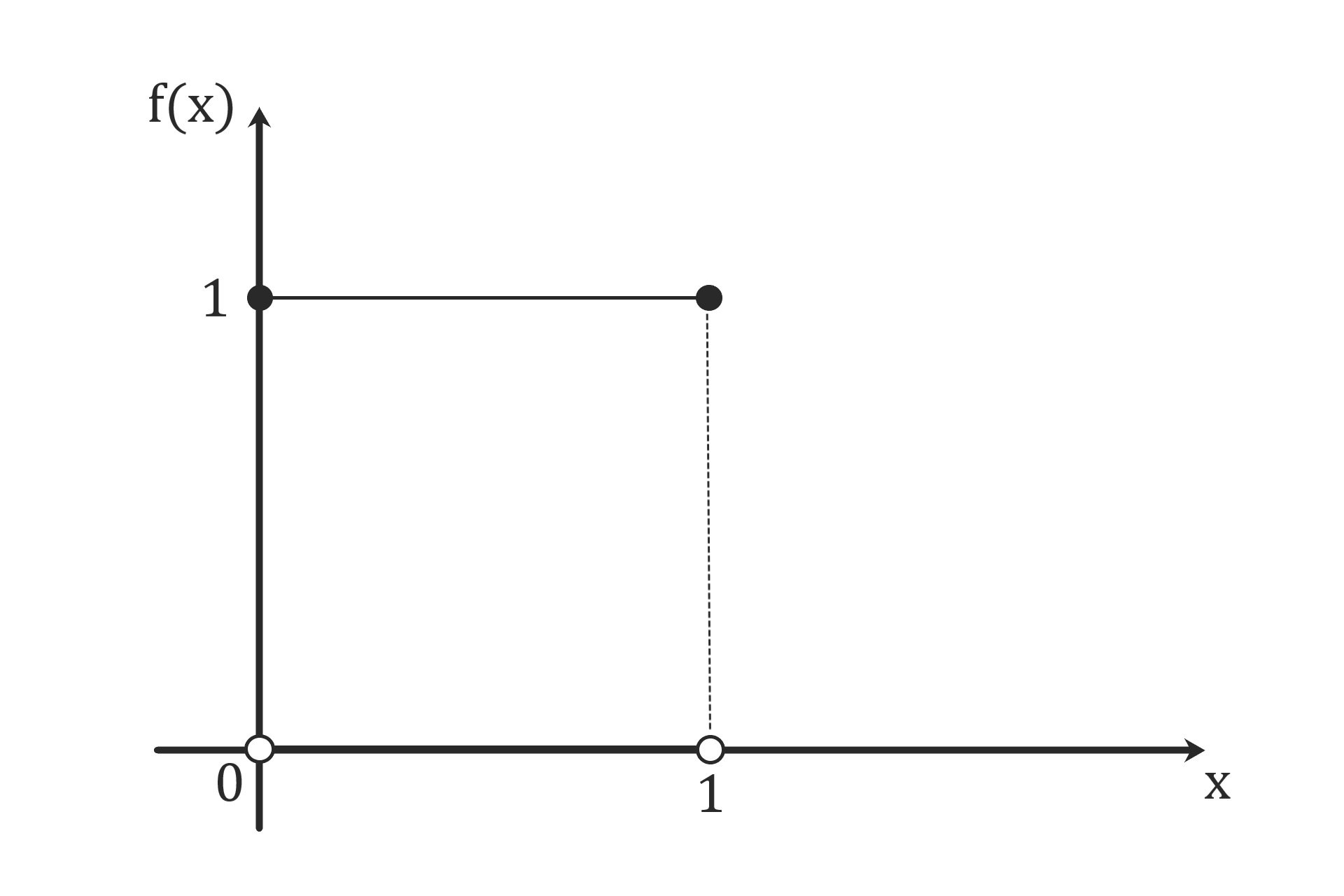
宅急便を例に説明します。

日時指定により、

午後０時～１時のランダムな時間に
配達員の人が現れるとします。

配達員の人が

• 午後0.5時（12時半）に現れたらXの値は0.5
• 午後0.1時（12時6分）に現れたらXの値は0.1
• 午後0.1666…時（12時10分）に現れたらXの値は0.1666…

と言った具合に
時間をそのままXの値に採用すれば、

各々の確率は等しく定まっているので

Xは０～１の小数を値に持つ確率変数となります。

２番目の文章の意味

「確率P(a≦X≦b)が定まっている」とは

具体的には、
ある確率密度関数f(x)が与えられていて

任意のa、bに対して

$$ P(a \leq X \leq b) = \int_a^b f(x) dx $$

が満たされる事を意味します。

宅急便の例だと

$$ f(x) = \left\{ \begin{eqnarray} &1& \quad (x \in [0, 1]) \\ &0& \quad (x \notin [0, 1]) \end{eqnarray} \right. \hspace{20cm}$$

です。

配達員の人が午後０時～0.1時に現れる確率は

$$ \int_0^{0.1} 1 \, dx = \big[ x \big]_0^{0.1} = 0.1 \hspace{20cm}$$

午後0.5時～0.8時に現れる確率は

$$ \int_{0.5}^{0.8} 1 \, dx= \big[ x \big]_{0.5}^{0.8} = 0.3 \hspace{20cm}$$

午後０時～１時に現れる確率は

$$ \int_0^1 1 \, dx = \big[ x \big]_0^{1} = 1 \hspace{20cm}$$

正しく計算できています。

離散との注意点

離散の時とは異なり
連続変数の確率は範囲でのみ求められます。

起きる事象が無限にあるので、

点での確率pを与えてしまうと

\( p \times \infty = \infty \)

全事象の確率の合計が１とはならず
無限大に発散してしまうからです。

連続変数についての確率密度関数は
積分した際、正しい確率が求まるよう書かれます。

離散変数についての確率密度関数は
点での値を見るだけで大丈夫です。

測度論的確率論大学生向けの話

確率変数が本質的にしている事は
事象と数との対応、つまり写像です。

本格的な確率変数の定義には写像を使います。

興味のある人におすすめ。

まとめ

確率変数とは

事象に数字という記号を与え、
数学を通して理解する仕組みです。

離散変数と連続変数の２種類あり、

前者は直感的に理解しやすい一方

後者は確率密度関数の積分で
確率を求める必要がある分難しいです。

高校数学の定義で十分
実際の仕事に役立ちますが、

大学ではさらに厳密な定義をします。

参考文献