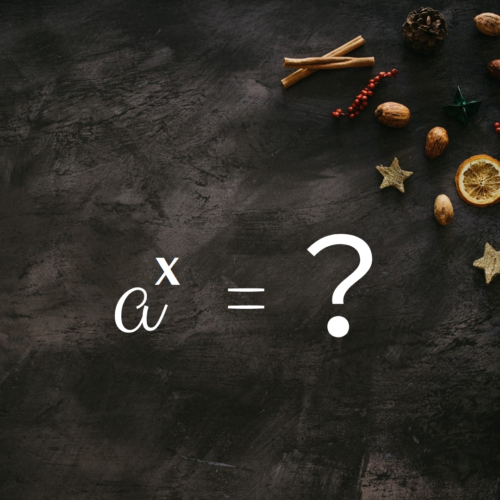テイラー展開(マクローリン展開)の公式をまとめてます。
一般項、展開式の成り立つxの範囲、
収束するかチェックできる様に
剰余項(ラグランジュの剰余)を書いて
また、私の理解の浅い部分は参考サイトを載せました。
↓剰余項の欄がないものは項別積分から求めます。
記事の終わりでは軽くテイラー展開
自体の説明もしたいと思います。
指数関数
\( e^x \)
$${e}^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\cdots \hspace{20cm}$$
xの範囲
\( |x| < \infty \)
剰余項
$$ \frac{e^{\theta x}}{n!}x^n \hspace{20cm} $$
一般形
$$\begin{eqnarray} a^x &=& \exp(x \ln a) \\ &=& \sum_{n=0}^{\infty}\frac{(x\ln a)^n}{n!} \\ &=& 1+x\ln a+\frac{(x\ln a)^2}{2!}+\frac{(x\ln a)^3}{3!}+\cdots \end{eqnarray} \hspace{20cm}$$
xの範囲
\( |x| < \infty \)
剰余項
$$ \frac{a^{\theta x}}{n!}(x \ln a)^n \hspace{20cm} $$
対数関数
\( \ln (1+x) \)
$$ \ln(1+x) =\sum_{n=1}^{\infty} \frac{(-1)^{n+1}x^n}{n} = x -\frac{x^2}{2} +\frac{x^3}{3} -\frac{x^4}{4} + \cdots \hspace{20cm} $$
xの範囲
\( -1<x \leq 1 \)
剰余項
$$ \frac{(-1)^{n+1}x^n}{n(1+\theta x)^n} \hspace{20cm} $$
コーシーの剰余
$$ \frac{(-1)^{n+1}}{(1+\theta x)^n}(1-\theta)^{n-1} x^n \hspace{20cm} $$
-1<x<0の時の収束を示すために使います。
\( \ln \left( \frac{1+x}{1-x} \right) \)
$$\begin{eqnarray} \ln \left( \frac{1+x}{1-x} \right) &=& \sum_{n=0}^\infty \frac{2}{2n+1} x^{2n+1} \\ &=& 2x +\frac{2}{3}x^3 +\frac{2}{5}x^5 +\frac{2}{7}x^7 +\cdots \end{eqnarray}\hspace{20cm} $$
対数の値を求めるための式です。
xの範囲
\( |x| < 1 \)
詳しく
\( \frac{1}{1-x^2} \)
$$ \frac{1}{1-x^2} = \sum_{n=0}^\infty x^{2n} = 1 +x^2 +x^4 +x^6 +\cdots \hspace{20cm} $$
対数のテイラー展開に関連します。
xの範囲
\( |x| < 1 \)
三角関数
\( \sin x \)
$$\sin x=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n+1}}{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots \hspace{20cm}$$
xの範囲
\( |x| < \infty \)
剰余項
$$ (-1)^n \frac{\cos (\theta x)}{(2n+1)!} x^{2n+1} \hspace{20cm} $$
\( \cos x \)
$$\cos x=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n}}{(2n)!}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots \hspace{20cm}$$
xの範囲
\( |x| < \infty \)
剰余項
$$ (-1)^{n+1} \frac{\cos (\theta x)}{(2n)!} x^{2n} \hspace{20cm} $$
\( \tan x \)
$$\tan x=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}}{(2n)!}x^{2n-1}\hspace{20cm}$$
$$\quad \quad \,\,\, =x+\frac{1}{3}x^3+\frac{2}{15}x^5+\frac{17}{315}x^7+\cdots\hspace{20cm}$$
ここで\(B_{2n}\)はベルヌーイ数。
$$ B_n := \sum_{k=0}^n \sum_{r=0}^k (-1)^r \begin{pmatrix} k \\ r \end{pmatrix} \frac{r^n}{k+1} \hspace{20cm} $$
ベルヌーイ数についての記事です。
xの範囲
$$ |x| < \frac{\pi}{2} \hspace{20cm} $$
参考サイト
- Stack Exchange「Formula for the...」
- Wikipedia「Bernoulli number」
- Wolfram MathWorld「Bernoulli Number」
- 高校数学の美しい物語「tanxの高階微分と…」
逆三角関数
\( \arcsin x \)
$$ \arcsin x = \sum_{n=0}^\infty \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1} \hspace{20cm}$$
$$\quad \quad \quad \! \left( = \sum_{n=0}^\infty \frac{\Gamma (n+\frac{1}{2})}{\sqrt{\pi}(2n +1)n!} x^{2n +1} \right) \hspace{20cm}$$
$$\quad \quad \quad \;\; = x +\frac{1}{6}x^3 +\frac{3}{40}x^5 +\frac{5}{112}x^7 +\frac{35}{1152}x^9 +\cdots \hspace{20cm} $$
ここで\( \Gamma (n+\frac{1}{2}) \)はガンマ関数。
$$ \Gamma (x) := \int_0^\infty t^{x-1} e^{-t} dt \hspace{20cm} $$
xの範囲
\( |x| < 1 \)
\( \arccos x \)
$$\begin{eqnarray} \arccos x &=& \frac{\pi}{2} -\arcsin x \\ &=& \frac{\pi}{2} -\sum_{n=0}^\infty \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1} \\ &=& \frac{\pi}{2} -x -\frac{1}{6}x^3 -\frac{3}{40}x^5 -\frac{5}{112}x^7 -\frac{35}{1152}x^9 -\cdots \end{eqnarray} \hspace{20cm} $$
xの範囲
\( |x| < 1 \)
\( \arctan x \)
$$\begin{eqnarray} \arctan x &=& \sum_{n=0}^\infty \frac{(-1)^{n}}{2n+1} x^{2n +1} \\ &=& x -\frac{1}{3}x^3 +\frac{1}{5}x^5 -\frac{1}{7}x^7 +\cdots \end{eqnarray} \hspace{20cm} $$
xの範囲
\( |x| \leq 1 \)
参考サイト
双曲線関数
\( \sinh x \)
$$\begin{eqnarray} \sinh x &=& \frac{e^x - e^{-x}}{2} \\ &=& \sum_{n=0}^\infty \frac{1}{(2n+1)!} x^{2n+1} \\ &=& x +\frac{1}{3!}x^3 +\frac{1}{5!}x^5 +\frac{1}{7!}x^7 +\cdots \end{eqnarray} \hspace{20cm} $$
exの展開式の奇数項と一緒です。
xの範囲
\( |x| < \infty \)
剰余項
$$ \frac{e^{\theta x} - (-1)^ne^{-\theta x}}{2n!} x^n \hspace{20cm} $$
\( \cosh x \)
$$\begin{eqnarray} \cosh x &=& \frac{e^x + e^{-x}}{2} \\ &=& \sum_{n=0}^\infty \frac{1}{(2n)!} x^{2n} \\ &=& 1 +\frac{1}{2!}x^2 +\frac{1}{4!}x^4 +\frac{1}{6!}x^6 +\cdots \end{eqnarray} \hspace{20cm} $$
exの展開式の偶数項と一緒です。
xの範囲
\( |x| < \infty \)
剰余項
$$ \frac{e^{\theta x} + (-1)^ne^{-\theta x}}{2n!} x^n \hspace{20cm} $$
\( \tanh x \)
$$\begin{eqnarray} \tanh x &=& \sum_{n=1}^\infty \frac{2^{2n}(2^{2n}-1)B_{2n}}{(2n)!} x^{2n-1} \\ &=& x -\frac{1}{3}x^3 +\frac{2}{15}x^5 -\frac{17}{315}x^7 +\frac{62}{2835}x^9 +\cdots \end{eqnarray} \hspace{20cm} $$
xの範囲
$$ |x| < \frac{\pi}{2} \hspace{20cm} $$
参考サイト
逆三角関数、双曲線関数の式の出典です。
分数
\( \frac{1}{1-x} \)
$$ \frac{1}{1-x} = \sum_{n=0}^\infty x^n = 1 +x +x^2 +x^3 +\cdots \hspace{20cm}$$
xの範囲
\( |x|<1 \)
剰余項
$$ \frac{1}{(1-\theta x)^{n+1}} x^n \hspace{20cm} $$
コーシーの剰余
$$ n \cdot \frac{(1-\theta)^{n-1} }{(1-\theta x)^{n+1}} x^n \hspace{20cm} $$
一般形
$$\begin{eqnarray} (1+x)^\alpha &=& \sum_{n=0}^\infty \begin{pmatrix} \alpha \\ n \end{pmatrix} x^n \\ &=& 1 +\alpha x +\frac{\alpha(\alpha -1)}{2!} x^2 +\frac{\alpha(\alpha -1)(\alpha -2)}{3!} +\cdots \end{eqnarray} \hspace{20cm} $$
xの範囲
任意の実数αについて、
\( |x|<1 \)
で収束します。
α=-1、xを-xで置き換えた物が前の式です。
一般2項係数
ここで一般2項係数は
$$ \begin{pmatrix} \alpha \\ 0 \end{pmatrix} := 1, \quad \begin{pmatrix} \alpha \\ n \end{pmatrix} := \frac{\alpha(\alpha-1)\cdots(\alpha -n +1)}{n!} \hspace{20cm} $$
と定義されます。
剰余項
\( \begin{pmatrix} \alpha \\ n \end{pmatrix} (1+\theta x)^{\alpha -n} x^n \)
コーシーの剰余
\( n \cdot \begin{pmatrix} \alpha \\ n \end{pmatrix} (1+\theta x)^{\alpha -n} (1- \theta)^{n-1} x^n \)
収束を示すにはコーシーの剰余を使います。
ルート
\( \sqrt{1+x} \)
上の一般形においてα=1/2とすれば、
$$\begin{eqnarray} \sqrt{1+x} = 1 &+&\frac{1}{2} x +\frac{1 \cdot (-1)}{2^2 \cdot 2!} x^2 +\frac{1 \cdot (-1) \cdot (-3)}{2^3 \cdot 3!} x^3 +\cdots \\ &+&\frac{1 \cdot (-1) \cdots (-2n +3) }{2^n \cdot n!} x^n +\cdots \end{eqnarray} \hspace{20cm} $$
\( \frac{1}{\sqrt{1-x}} \)
α=-1/2、xを-xで置き換えると
$$\begin{eqnarray} \frac{1}{\sqrt{1-x}} = 1 &+&\frac{1}{2} x +\frac{1 \cdot 3}{2^2 \cdot 2!} x^2 +\frac{1 \cdot 3 \cdot 5}{2^3 \cdot 3!} x^3 +\cdots \\ &+&\frac{1 \cdot 3 \cdots (2n-1) }{2^n \cdot n!} x^n +\cdots \end{eqnarray} \hspace{20cm} $$
arcsin(x)のテイラー展開に利用します。
テイラー(Taylor)の定理
最後にテイラー展開の基礎知識を説明して
まとめようと思います。
f(x)は区間[a, b]においてn-1回連続微分可能で、
(a, b)においてn回微分可能とする。
この時、あるξ∈(a, b)が存在し
f(b)は次の様に展開される。
aとbを入れ換えた式も同様に成立する。
閉区間における微分可能
ここで閉区間[a, b]において微分可能とは、
[a, b]上の関数f(x)が
内部の開区間(a, b)において微分可能かつ
x=aの右側微係数
$$ \lim_{h \to +0} \frac{f(a+h)-f(a)}{h} \hspace{20cm} $$
x=bの左側微係数
$$ \lim_{h \to -0} \frac{f(b+h)-f(b)}{h} \hspace{20cm} $$
が共に存在することを言います。
定理の解説
テイラーの定理を初めて見ると
複雑な展開式で戸惑うと思いますが、
b=x、a=0の時を考えると分かりやすいです。
$$ \begin{eqnarray} f(x) = f(0) &+& f'(0)x + \frac{f''(0)}{2!} x^2 + \cdots \\&+& \frac{f^{(n-1)}(0)}{(n-1)!} x^{n-1} + \frac{f^{(n)}(\xi)}{n!} x^n \end{eqnarray} \hspace{20cm}$$
これを用いて
例えばf(x)=x3+x2+x+1を展開してみます。
$$\begin{eqnarray} f(x) = (&0^3& +0^2 +0 + 1) +(3 \cdot 0^2 +2 \cdot 0 +1)x \\ &+&\frac{3 \cdot 2 \cdot 0 +2 \cdot 1 }{2!}x^2 +\frac{3 \cdot 2 \cdot 1}{3!}x^3 +0 + \cdots +0 +0 \end{eqnarray} \hspace{20cm}$$
\( \quad \quad \; \, = 1 +x +x^2 +x^3 \)
となり、
xのn次式については
自明に成り立つ定理なことが観察されます。
どんなn次式も昇べきの順に出て来ます。
この展開式が実は、
一般のn回微分可能な関数(exやsinxなど)
にも使えることに気付いたのが
テイラーさんの凄い所だと思います。
- ロール(Rolle)の定理
- 平均値の定理(mean value theorem)
も定理の発見に大きく貢献しました。
テイラー展開
テイラーの定理の末項
$$ R_n = \frac{f^{(n)}(\xi)}{n!} (b-a)^n \hspace{20cm} $$
は剰余項と呼ばれます。
もし剰余項が無限大で0に収束していれば、
無限級数
$$f(a) + f'(a)(b-a) + \frac{f''(a)}{2!} (b-a)^2 + \frac{f^{(3)}(a)}{3!} (b-a)^3 + \cdots \hspace{20cm}$$
はf(b)に収束するので
$$ f(b) = \sum_{n=0}^\infty \frac{f^{(n) }(a) }{n!}(b-a)^n \hspace{20cm}$$
と書けます。
上式をb=x、a=x0で置き換えた式
$$ f(x) = \sum_{n=0}^\infty \frac{f^{(n) }(x_0) }{n!}(x-x_0)^n \hspace{20cm}$$
をf(x)のx0を中心としたテイラー展開と呼びます。
マクローリン展開
特に0を中心としたテイラー展開
$$ f(x) = \sum_{n=0}^\infty \frac{f^{(n) }(0) }{n!}x^n \hspace{20cm}$$
はマクローリン展開と呼ばれ、
最も良く使われます。
単にテイラー展開と言う時は、
マクローリン展開を指すことが多いです。
0を中心とし、テイラー展開しただけなので
マクローリン展開という呼び名を嫌う教授もいます。
剰余項
テイラー展開できるかは
剰余項の収束が鍵なので、細かく研究されています。
ラグランジュの剰余
$$ R_n = \frac{f^{(n)}(a +\theta (b-a))}{n!} (b-a)^n \hspace{20cm} $$
ここでθは(0<θ<1)を満たす、ある実数。
上の式はテイラーの定理の剰余項で
\( \xi = a +\theta (b-a) \)
と置き直したものです。
(a, b)の任意の点はa+θ(b-a)の形で書けます。
θの範囲が0と1の間なので計算しやすいことで優れます。
ロッシュ-シュレミルヒの剰余
$$ R_n = \frac{f^{(n)}(a +\theta (b-a))}{p(n-1)!} (1-\theta)^{n-p} (b-a)^n \quad (0<\theta<1) \hspace{20cm} $$
ここでpは(0<p≦n)を満たす任意の実数。
ラグランジュの剰余の一般化が
ロッシュ-シュレミルヒの剰余です。
p=nでラグランジュの剰余になります。
コーシーの剰余
$$ R_n = \frac{f^{(n)}(a +\theta (b-a))}{(n-1)!} (1-\theta)^{n-1} (b-a)^n \quad (0<\theta<1) \hspace{20cm} $$
p=1の時がコーシーの剰余です。
(1-θ)n-1の項を収束の計算に利用する際、良く使われます。