三角形の面積は
底辺×高さ÷2、三角関数、法線ベクトル、ヘロンの公式
など沢山の方法で求まります。
行列式を用いると
3次元空間内の三角形の
頂点の座標が分かっている時
最も速く汎用性高く
計算する事ができます。
始めに、平面上の三角形から説明して
空間内の三角形へと繋げます。
線形代数の基礎、行列式
定理の証明はかなり難しいです。
3点が同一平面上にある場合
原点を頂点に持つ三角形
三角形の面積(基本)
原点O(0, 0)、点A(a1, a2)、点B(b1, b2)
により作られる三角形の面積は
$$ \frac{1}{2}\times \left| det \begin{bmatrix} a_1 & a_2 \\ b_1 & b_2 \end{bmatrix} \right| \quad \left(= \frac{1}{2} | a_1 b_2 -a_2 b_1 | \right) \hspace{20cm}$$
である。
証明
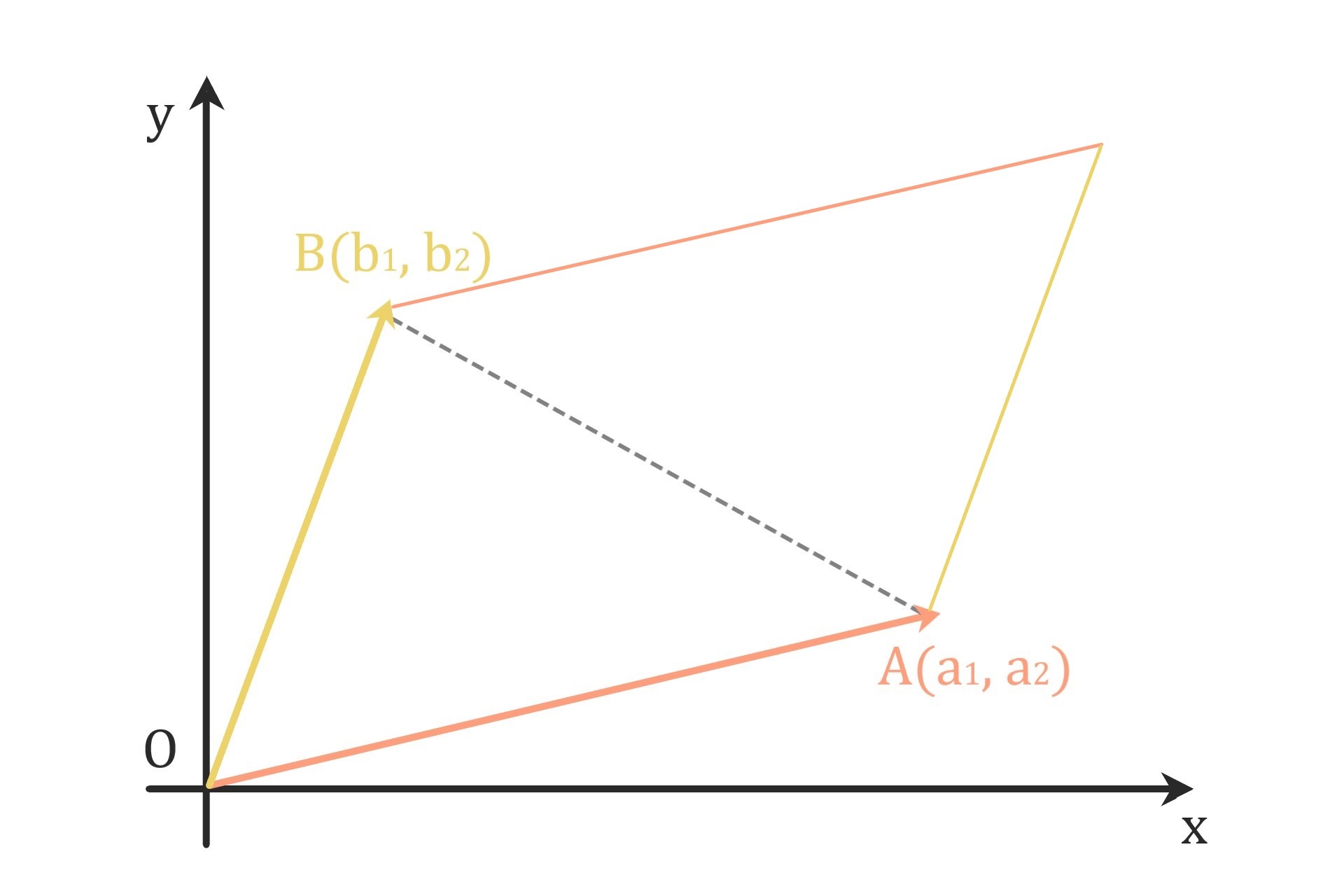
$$\left| det \begin{bmatrix} a_1 & a_2 \\ b_1 & b_2 \end{bmatrix} \right| \hspace{20cm}$$
は二つのベクトル
$$ \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}, \quad \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} \hspace{20cm}$$
で張られる平行四辺形の面積に等しい。
三角形OABの面積はその半分。\(\square\)
任意の三点を持つ三角形
三角形の面積(一般)
点A(a1, a2)、点B(b1, b2)、点C(c1, c2)
により作られる三角形の面積は
$$ \frac{1}{2}\times \left| det \begin{bmatrix} b_1 -a_1 & b_2 -a_2 \\ c_1 -a_1 & c_2 -a_2 \end{bmatrix} \right| \hspace{20cm}$$
である。
証明
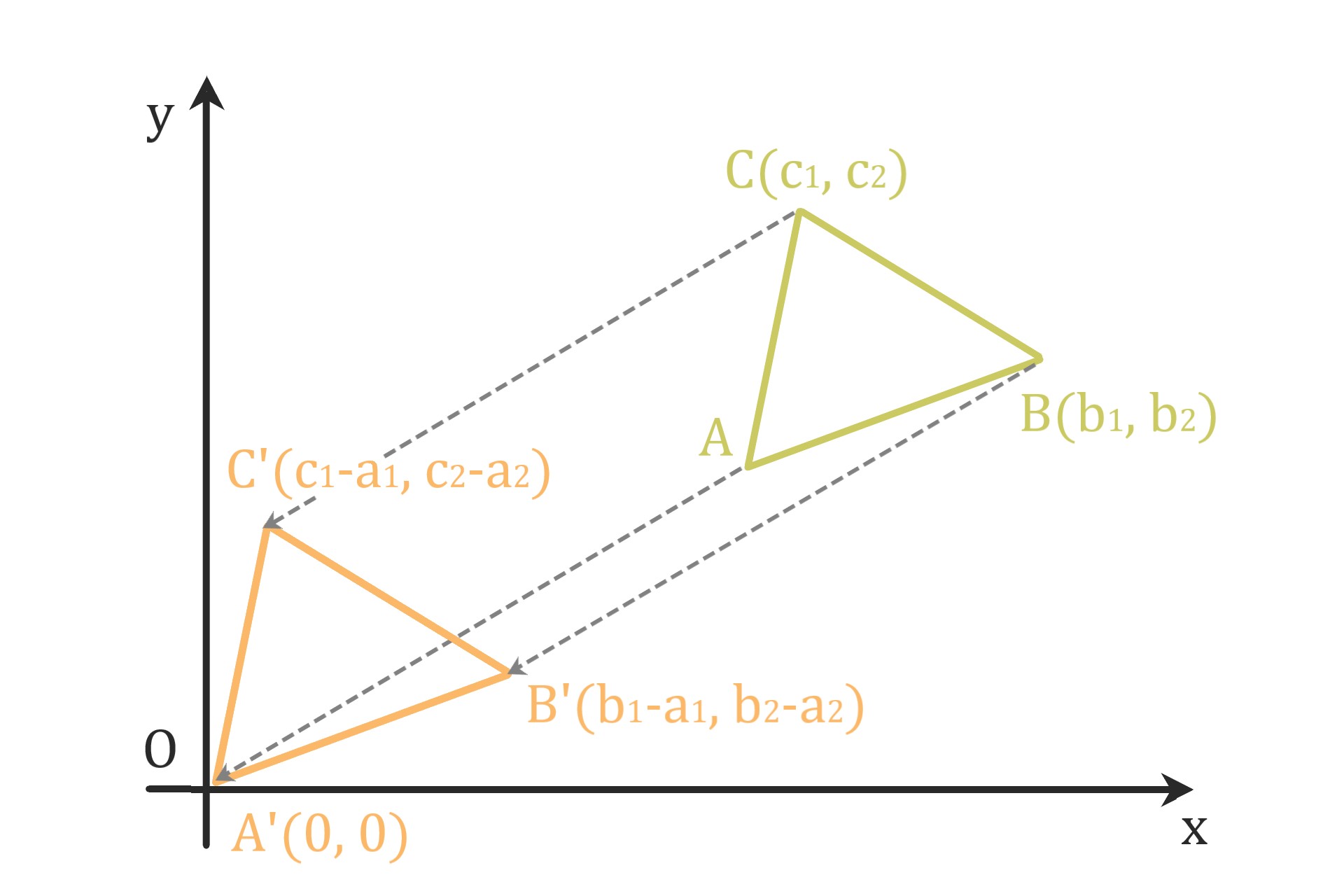
点A、B、Cをベクトル
$$ \begin{pmatrix} -a_1 \\ -a_2 \end{pmatrix} \hspace{20cm}$$
で平行移動させた点をA'、B'、C'とする。
座標はA'(0, 0)、B'(b1-a1, b2-a2)、C'(c1-a1, c2-a2)
かつ△ABC=△A'B'C'を満たす。
先の定理を三角形A'B'C'に適用して結論を得る。\(\square\)
サラスの方法を利用(発展)
実用性は低いものの
サラスの方法で計算する
綺麗な公式もあります。
三角形の面積(サラスの方法)
点A(a1, a2)、点B(b1, b2)、点C(c1, c2)
により作られる三角形の面積は
$$ \frac{1}{2}\times \left| det \begin{bmatrix} a_1 & a_2 & 1 \\ b_1 & b_2 & 1 \\ c_1 & c_2 & 1 \end{bmatrix} \right| \hspace{20cm}$$
である。
補題
図の様に描かれる三角錐OABCの体積は
ベクトルOA、OB、OCで張られる
平行六面体の体積の1/6である。
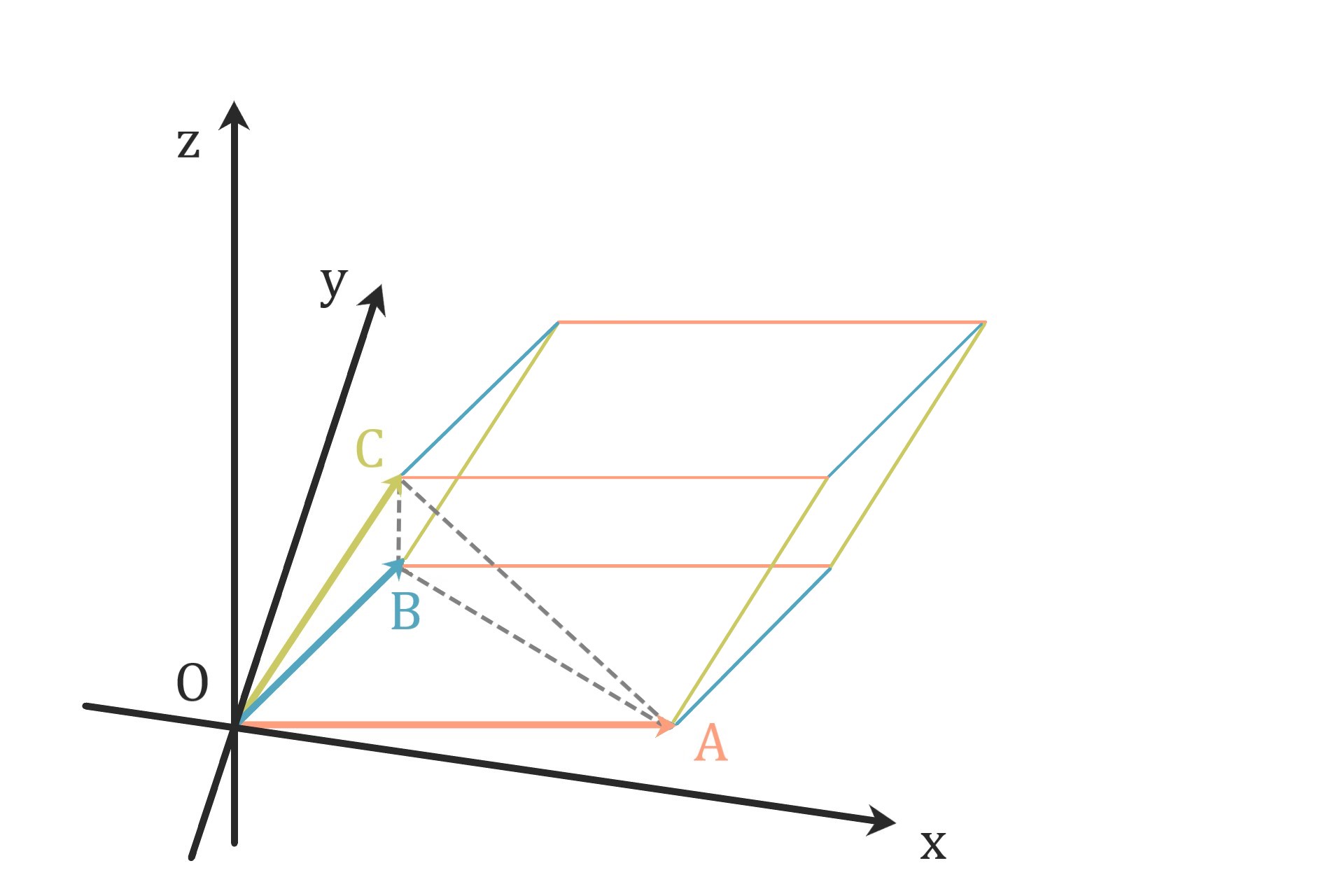
三角錐OABCの底面積は
平行六面体の底面積Sの半分、
高さhは共通なので
三角錐の体積=S×1/2×h×1/3
=(S×h)×1/6=平行六面体の体積×1/6 \(\square\)
証明
点A'(a1, a2. 1)、点B'(b1, b2, 1)、点C'(c1, c2, 1)を考える。
三角錐OA'B'C'は底面積△ABC、
高さ1を持つので体積は△ABC×1/3
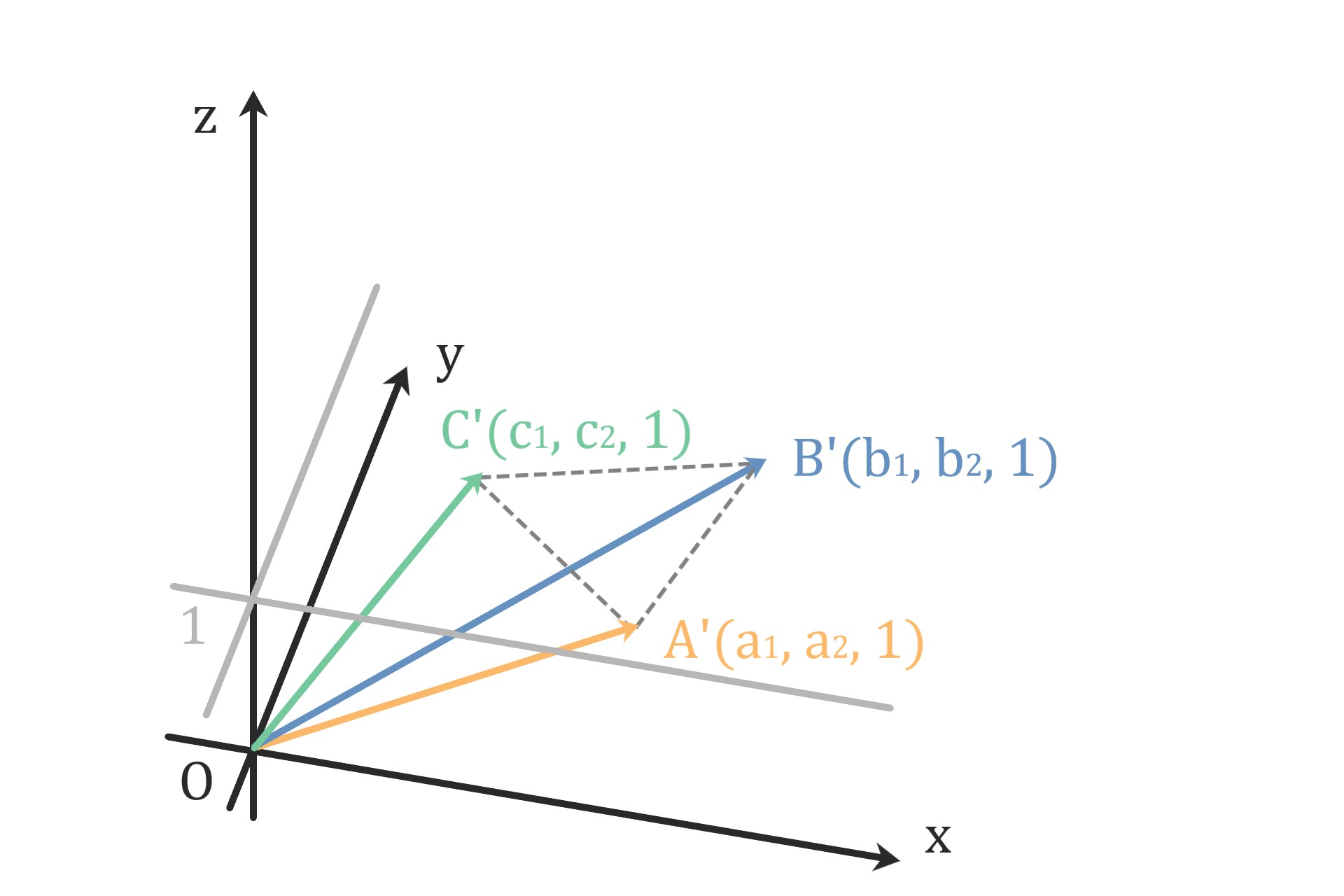
一方ベクトルOA'、OB'、OC'で張られる平行六面体の体積は
$$ \left| det \begin{bmatrix} a_1 & a_2 & 1 \\ b_1 & b_2 & 1 \\ c_1 & c_2 & 1 \end{bmatrix} \right| \hspace{20cm}$$
なので補題より結論を得る。\(\square\)
3点が同一平面上にない場合
座標空間内の任意の三角形の面積は、次の定理で求められます。
三角形の面積(3次元空間)
点A(a1, a2, a3)、点B(b1, b2, b3)、点C(c1, c2, c3)
により作られる三角形の面積は
$$A:= \begin{bmatrix} b_1 -a_1 & b_2 -a_2 & b_3 -a_3 \\ c_1 -a_1 & c_2 -a_2 & c_3 -a_3 \end{bmatrix} \hspace{20cm}$$
として
$$ \frac{1}{2}\times \sqrt{ det (A A^\top) } \hspace{20cm}$$
である。
証明および
平行四辺形の面積、
平行六面体の体積と
行列式との関係は
下の記事を参照ください。
まとめ
頂点の座標が与えられている時
行列式を用いると、
底辺、高さを飛ばして直接
面積を求められるので効率的です。
特に最後の定理は
任意の三角形に適用可能で
覚えておくと役に立ちます。
サラスの方法の公式は、
実用性は低いものの
線形代数の講義で
サラスの方法を学生に
練習させるため登場する事があります。

