
積分の値はリーマンの定義通りには求めづらく
一変数の場合、積分と微分が
逆の操作である事を利用して解きました。
重積分についても同様に難しく、
この場合は一変数の積分に分ける
逐次積分と呼ばれる方法をとります。
逐次積分は直感的には成立して当然かつ
条件も関数の連続性のみ
なので定理として忘れられがちです…。
この記事では逐次積分を学び直し
積分領域の範囲の定め方や順序交換、
ガウス積分、フビニの定理
との関連性まで書いて行きます。
逐次積分の定理
長方形
逐次積分の定理(長方形)
f(x, y)がΩ=[a, b]×[c, d]の上で連続ならば
$$ \iint_\Omega f(x, y) dx dy = \int_a^b \left( \int_c^d f(x, y) dy \right) dx \hspace{20cm}$$
長方形[a, b]×[c, d]における二重積分の値は
f(x, y)をcからdまでyについて積分した後、
aからbまでxについて積分すると求まります。
一般の図形
逐次積分の定理(一般の図形)
[a, b]上で連続な関数Φ1(x)、Φ2(x)は
\( \forall x \in [a, b], \quad \phi_1 (x) < \phi_2 (x) \)
を満たすとする。
この時、閉領域
\( \Omega := \{ (x, y) \, | \, a \leq x \leq b, \quad \phi_1(x) \leq y \leq \phi_2 (x) \} \)
の上でf(x, y)が連続ならば
$$ \iint_\Omega f(x, y) dx dy = \int_a^b \left( \int_{\phi_1 (x)}^{\phi_2 (x)} f(x, y) dy \right) dx \hspace{20cm} $$
一般の図形の場合は始めに
xまたはy座標のどちらかを基準に、
積分したい領域を
二つの連続関数Φ1、Φ2で挟み込みます。
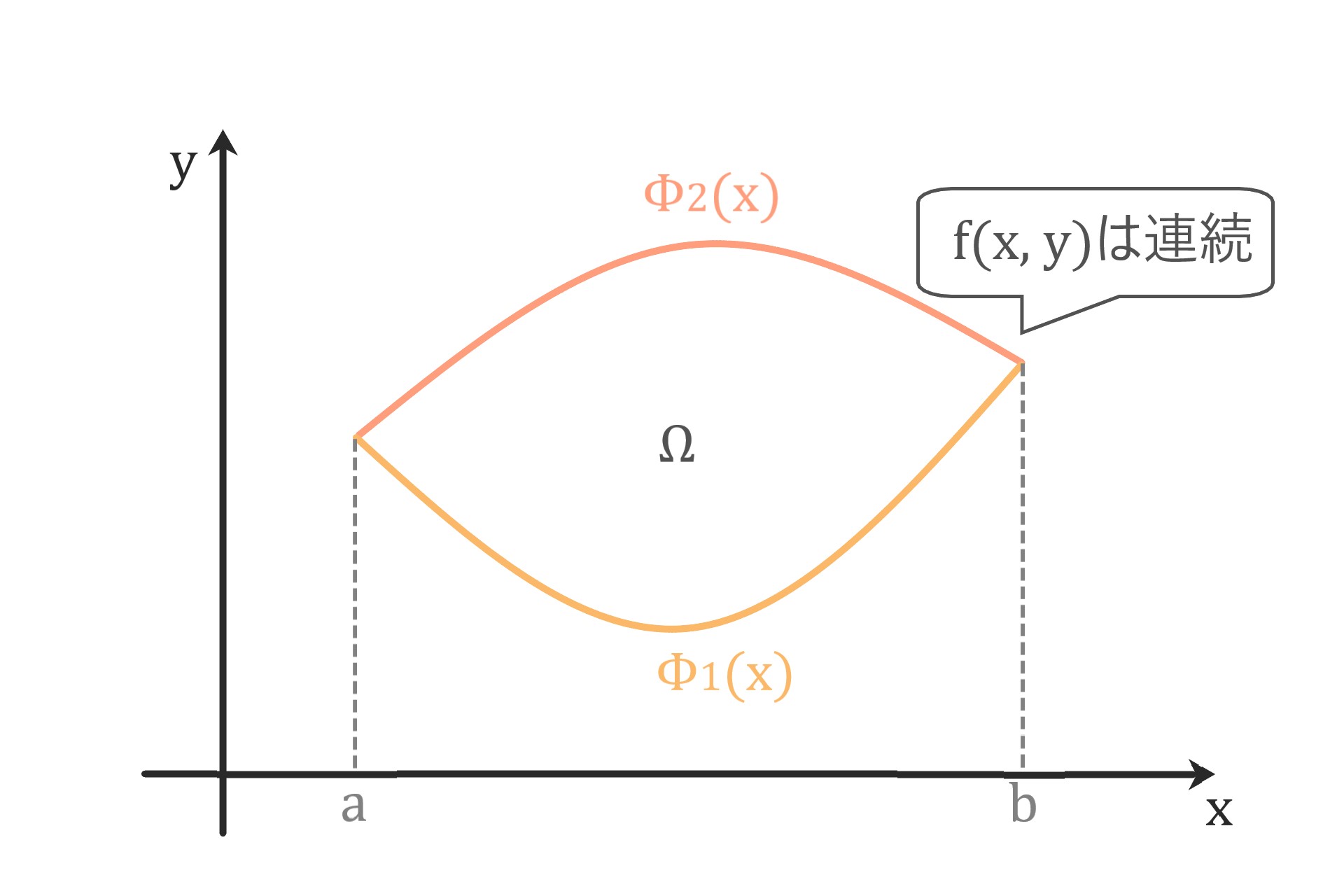
f(x, y)をΦ1(x)からΦ2(x)までyについて積分した後、
aからbまでxについて積分すると求まります。
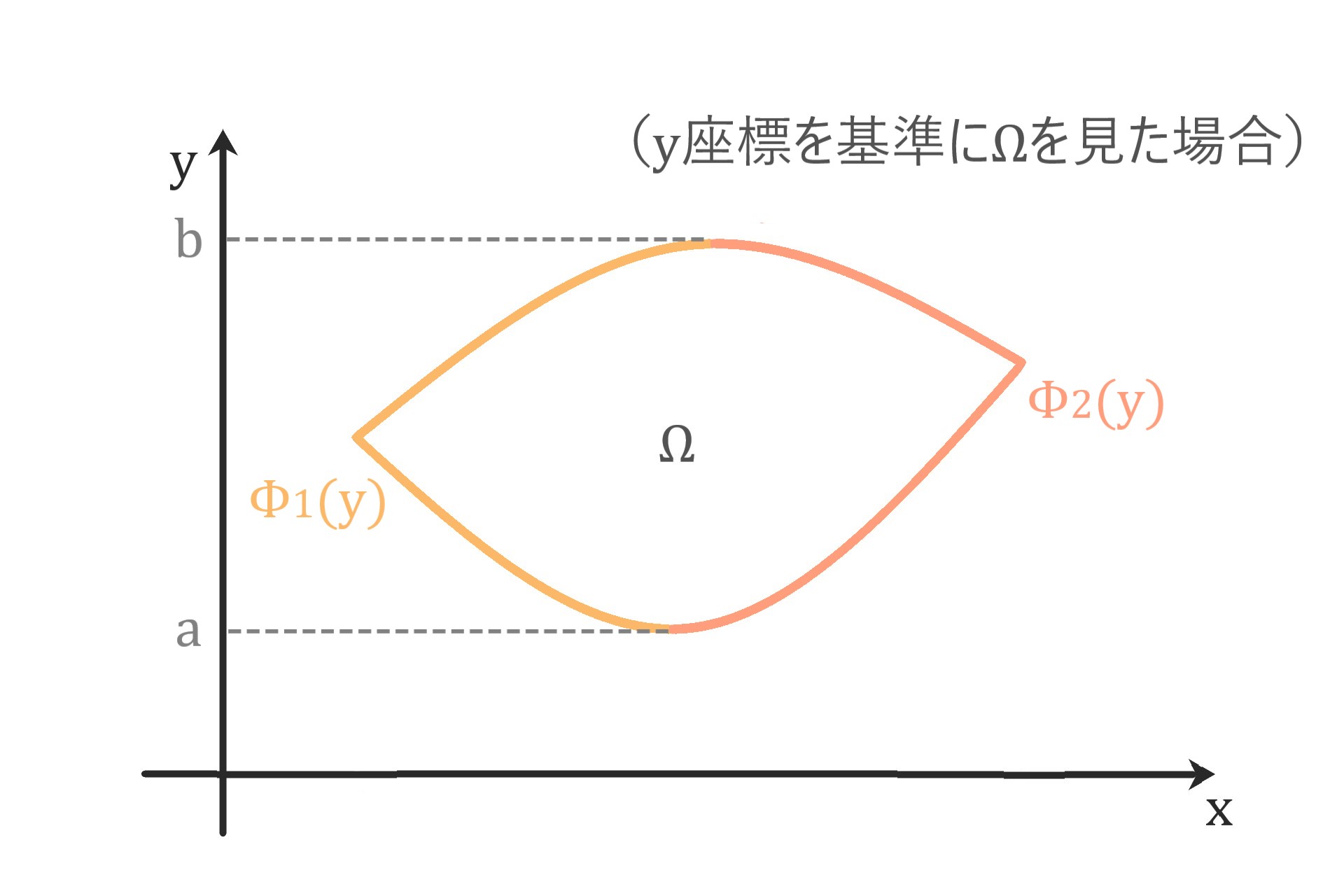
y座標を基準にした時も同様で
f(x, y)をΦ1(y)からΦ2(y)までxについて積分した後、
aからbまでyについて積分すると求まります。
積分の順序交換
定理を使うための条件は
積分領域において関数が連続である事だけです。
xとyを入れ換えても仮定は保たれるので、
順序交換の等式が得られます。
長方形における積分も
$$ \int_a^b \left( \int_c^d f(x, y) dy \right) dx = \int_c^d \left( \int_a^b f(x, y) dx \right) dy \hspace{20cm}$$
の様にxとyの、どちらから計算しても大丈夫です。
多次元
逐次積分の定理(3次元)
[a, b]上で連続な関数Φ1(x)、Φ2(x)は
\(\forall x \in [a, b], \quad \phi_1 (x) < \phi_2 (x) \)
を満たすとする。
さらに閉領域
\( D := \{ (x, y) \, | \, a \leq x \leq b, \quad \phi_1(x) \leq y \leq \phi_2 (x) \} \)
上で連続な関数ψ1(x, y)、ψ2(x, y)は
\(\forall (x, y) \in D, \quad \psi_1 (x, y) < \psi_2 (x, y) \)
を満たすとする。
この時、閉領域
\( \Omega := \{ (x, y, z) \, | \, (x, y) \in D, \quad \psi_1(x, y) \leq z \leq \psi_2 (x, y) \} \)
の上でf(x, y, z)が連続ならば
$$ \iiint_\Omega f(x, y, z) dx dy dz \hspace{20cm}$$
$$= \int_a^b \left( \int_{\phi_1 (x)}^{\phi_2 (x)} \left( \int_{\psi(x, y)}^{\psi(x, y) } f(x, y, z) dz \right) dy \right) dx $$
体積積分については
途中まで面積分の時と同じに進めた後、
連続関数ψ1、ψ2を用意して
3次元の積分領域を定めます。
n次元についても、この操作の繰り返しです。
二つの連続関数により次元を上げて行って
最後に出来上がった閉領域上で
関数が連続なら逐次積分できます。
どの変数から閉領域を定めても良く
積分の順序交換が可能です。
逐次積分の系→応用
逐次積分の定理には
応用数学の大事な系があります。
逐次積分(かけ算)
Ω=[a, b]×[c, d]において関数f(x, y)が
[a, b]上で連続なxの関数g(x)と
[c, d]上で連続なyの関数h(y)の積、
すなわち
\( f(x, y)=g(x) h(y) \)
の様に書かれるなら
$$ \iint_\Omega f(x, y) dx dy = \int_a^b g(x) dx \int_c^d h(y) dy \hspace{20cm}$$
証明
g(x)、h(y)は連続なのでf(x, y)もΩの上で連続。
逐次積分の定理より
$$ \iint_\Omega f(x, y) dx dy = \int_c^d \left( \int_a^b f(x, y) dx \right) dy \hspace{20cm}$$
$$\quad \quad \quad \quad\quad\quad \quad = \int_c^d \left( \int_a^b g(x) h(y) dx \right) dy \hspace{20cm}$$
xの積分においてh(y)は定数と見做せるから、
$$ = \int_c^d h(y) \left( \int_a^b g(x) dx \right) dy \hspace{20cm}$$
また
$$ \int_a^b g(x) dx \hspace{20cm}$$
は定数だから
$$ = \int_a^b g(x) dx \int_c^d h(y) dy \quad \square \hspace{20cm}$$
中心極限定理への応用
この系は統計学の中心極限定理
を示すのに必要な
次の公式を導いてくれます。
証明は少しトリッキーで、
最初に二乗した値を求めます。
$$\left( \int_\mathbb{R} e^{-x^2/2} dx \right)^2 = \int_\mathbb{R} e^{-x^2/2} dx \int_\mathbb{R} e^{-y^2/2} dy \hspace{20cm} $$
系より
$$ = \iint_{\mathbb{R}^2} e^{-x^2/2} e^{-y^2/2} dx dy = \iint_{\mathbb{R}^2} e^{-(x^2 +y^2)/2} dx dy \hspace{20cm}$$
Rは無限区間なので厳密には
有限の閉区間に適用した後、極限をとります。
極座標変換すると
$$ = \iint e^{-r^2/2} \, |r| \, dr d\theta = \iint \frac{d}{dr} (- e^{-r^2/2} ) dr d\theta = 2 \pi \hspace{20cm}$$
両辺のルートをとれば完成です。
↓極座標変換についての記事です。

フビニの定理について
ルベーグ積分にも逐次積分はあって
フビニの定理と言います。
これに倣って、
リーマン積分の逐次積分の定理も
しばしばフビニの定理と呼ばれます。
まとめ
重積分の値は一変数の積分を繰り返す
逐次積分により求めることが出来ます。
微分は定義通りで良いのに、
積分は区分求積法みたく
素直に計算しようとすると
難しくなるのは不思議ですね。

