
空気中を伝搬する音の減衰する理由は主に
音の範囲が広がることによるエネルギーの分散と
空気吸収の2つです。
このうち空気吸収の計算方法は
ISO9613-1(1993年)から規格が出ていて
日本だとJIS Z8738(1999年)に載っています。
またJISの原案作成に携わった
吉久光一先生のこちらのPDFも勉強になります。
この記事では
それらの要点を抜き出して
わかりやすく解説したいと思います。
空気吸収の式
音圧による理解
音の減衰は指数関数的であり
平面音波が空気中を進んで減衰した後の音圧は
減衰係数と呼ばれる物を用いて次の式で計算されます。
\( p_t = p_i \exp(-0.1151 \, \alpha s ) \)
- pi:始めの音圧[Pa]
- s:進んだ距離[m]
- pt:進んだ後の音圧[Pa]
- α:減衰係数[dB/m]
デシベルによる表記
上と同値な式に
$$ 10 \log_{10} \frac{p_t^2 }{p_i^2 } = -\alpha s $$
があります。
左辺はpiを基準にptを見たデシベルの定義式なので
平面音波は空気中を
1m進むごとにαデシベル減衰する
と理解できます。
減衰係数の単位が[dB/m]の理由です。
同値であることの証明
$$ 10 \log_{10} \frac{p_t^2 }{p_i^2 } = -\alpha s \hspace{20cm}$$
$$ \Leftrightarrow \log_{10} \frac{p_t }{p_i } = -\frac {\alpha s}{20} \hspace{20cm}$$
底10の指数にとって
$$ \Leftrightarrow \frac{p_t }{p_i } = 10^{-\alpha s/20} \hspace{20cm}$$
底がeの対数をとった後、底eの指数にとると元に戻るので
$$ \Leftrightarrow \frac{p_t }{p_i } =\exp \left( \frac{-\alpha s}{20} \ln 10 \right) \hspace{20cm}$$
ここで値
$$ \frac{\ln 10 }{20} \fallingdotseq 0.1151 \hspace{20cm}$$
を用いて
\( \Leftrightarrow p_t = p_i \exp(-0.1151 \, \alpha s ) \)
となる。\( \square \)
減衰係数
肝心な減衰係数ですが
- 平面音波の周波数
- 気温
- 気圧
- 相対湿度
によって定まります。
例えば気温20℃の減衰係数は次の通りです。
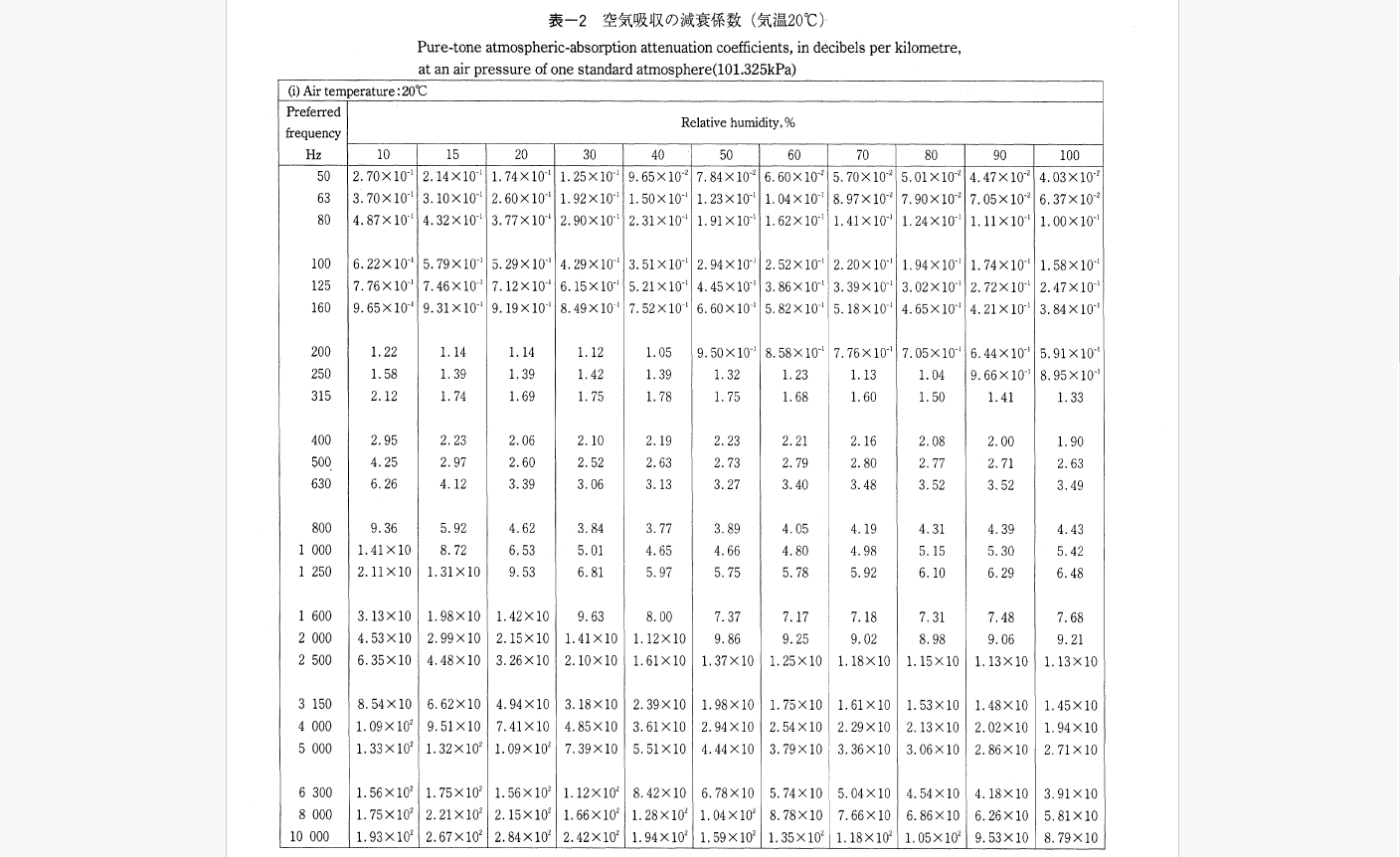
JIS Z8738には大気圧下における減衰係数の値が
気温-20℃から50℃まで5℃刻みで表になっています。
それを見れば音の減衰を先の式で計算する事が出来ます。
表の値は厳密な中心周波数で計算されたもの、若干のズレがあります。
減衰係数の計算式
減衰係数を求める式も載っているのですが、かなり複雑です。
減衰係数αは次の値です。
$$ \begin{split} 8.686 f^2 \left( \left[ 1.84 \times 10^{-11} \left( \frac{p_a}{p_r} \right)^{-1} \left( \frac{T}{T_0} \right)^{1/2} \right] + \left( \frac{T}{T_0} \right)^{ -5/2 } \\ \times \left\{ 0.01275 \left[ \exp \left( \frac{-2239.1 }{T} \right) \right] \left[ f_{rO} +\left( \frac{f^2}{f_{rO} } \right) \right]^{-1} \\ + 0.1068 \left[ \exp \left( \frac{ -3352.0}{T} \right) \right] \left[ f_{rN} +\left( \frac{f^2}{f_{rN} } \right) \right]^{-1} \right\} \right) \end{split} $$
- f:平面音波の周波数[Hz]
- pa:気圧[kPa]
- pr:基準の気圧(101.325[kPa]_大気圧)
- T:気温[K]
- T0:基準の気温(293.15[K]_20℃)
空気吸収の4つの原因
ここでfrOとfrNは酸素の緩和周波数、窒素の緩和周波数と呼ばれており
$$ f_{rO} = \frac{p_a}{p_r} \left( 24 +4.04 \times 10^4 h \frac{0.02+h }{0.391 +h } \right) \hspace{20cm}$$
$$ f_{rN} = \frac{p_a}{p_r} \left( \frac{T}{T_0} \right)^{-1/2} \hspace{20cm}$$
$$ \times \left( 9 +280h \exp \left\{ -4.170 \left[ \left( \frac{T}{T_0} \right)^{-1/3} -1 \right] \right\} \right) $$
- h:水蒸気モル濃度[%]
で求まります。
そもそも空気中で音が減衰する理由は
- 空気の粘性や熱伝導に起因する古典吸収
- 分子の回転緩和現象に起因する吸収
- 酸素分子の振動緩和現象に起因する吸収
- 窒素分子の振動緩和現象に起因する吸収
の4つで
空気の21%は酸素、78%は窒素が占めているだけあって
酸素と窒素の影響が特に大きいです。
そのためfrOとfrNが用意されているみたいです。
水蒸気モル濃度
計算には私たちが普段使っている湿度(相対湿度)
を水蒸気モル濃度に変換する必要もあります。
$$ h = h_r \cfrac{ \left( \cfrac{p_{sat }}{p_r} \right) }{ \left( \cfrac{p_a}{p_r} \right) } \hspace{20cm} $$
- hr:相対湿度[%]
- psat:飽和水蒸気圧(水面上)
飽和水蒸気圧は気温のみに依存し
その値は世界気象機関(WMO)の国際気象表などで確認できます。
もしくは近似値を式から導出することも可能です。
$$ \frac{p_{sat}}{p_r} = 10^C \hspace{20cm}$$
指数Cは
$$ C = -6.8346 \left( \frac{T_{01}}{T} \right)^{1.261} +4.6151 \hspace{20cm}$$
- T01:水の3重点273.16[K]_0.01℃
と書かれます。
これらをエクセル等に入力してPCに計算させれば
自分の手でも減衰係数の表を作れます。
高音ほど速やかに減衰する
減衰係数は先の
- 平面音波の周波数
- 気温
- 気圧
- 相対湿度
により値を変えるのですが
この中で一つだけ
周波数による変化はわかりやすいです。
すなわち減衰係数は周波数について単調増加します。
同じ音でも遠くで聞くと近くで聞いた時より
低い印象になる理由です。
証明
減衰係数の式はすべて
正の数の足し算と掛け算になっており
その中で周波数fが増えるごとに減っているのは
$$ \left[ f_{rO} +\left( \frac{f^2}{f_{rO} } \right) \right]^{-1} \hspace{20cm}$$
$$\left[ f_{rN} +\left( \frac{f^2}{f_{rN} } \right) \right]^{-1} \hspace{20cm}$$
のみ。
これらにはf2が掛かっているので実際は
$$ \quad f^2 \left[ f_{rO} +\left( \frac{f^2}{f_{rO} } \right) \right]^{-1}\hspace{20cm}$$
$$ = \left( \frac{1}{ f^2} \right)^{-1} \left[ f_{rO} +\left( \frac{f^2}{f_{rO} } \right) \right]^{-1}\hspace{20cm}$$
$$ = \left[ \frac{ f_{rO}}{f^2} +\left( \frac{1}{f_{rO} } \right) \right]^{-1}\hspace{20cm}$$
のようfについて単調増加する項になる。\( \square \)
実用的な求め方
JISの空気吸収の式は
周波数の定まった純音に対するものですが
普段、私たちの聞く音は
さまざまな周波数が混ざり合っていて
次のグラフみたくなっています。
この場合の減衰を求めるには
まず中心となる周波数を決めて
周波数帯ごとに分割、
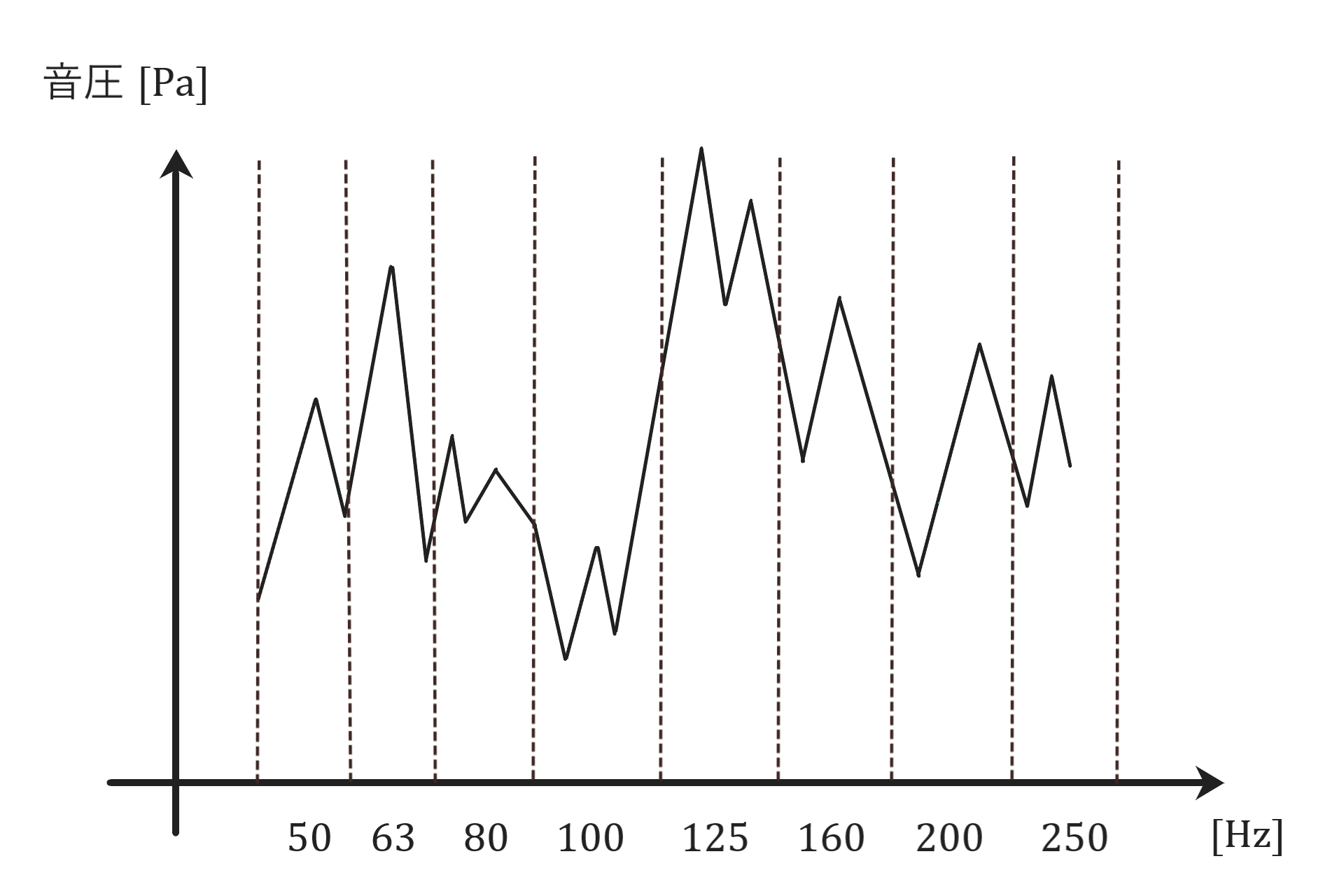
音圧を測定したグラフを手に入れます。
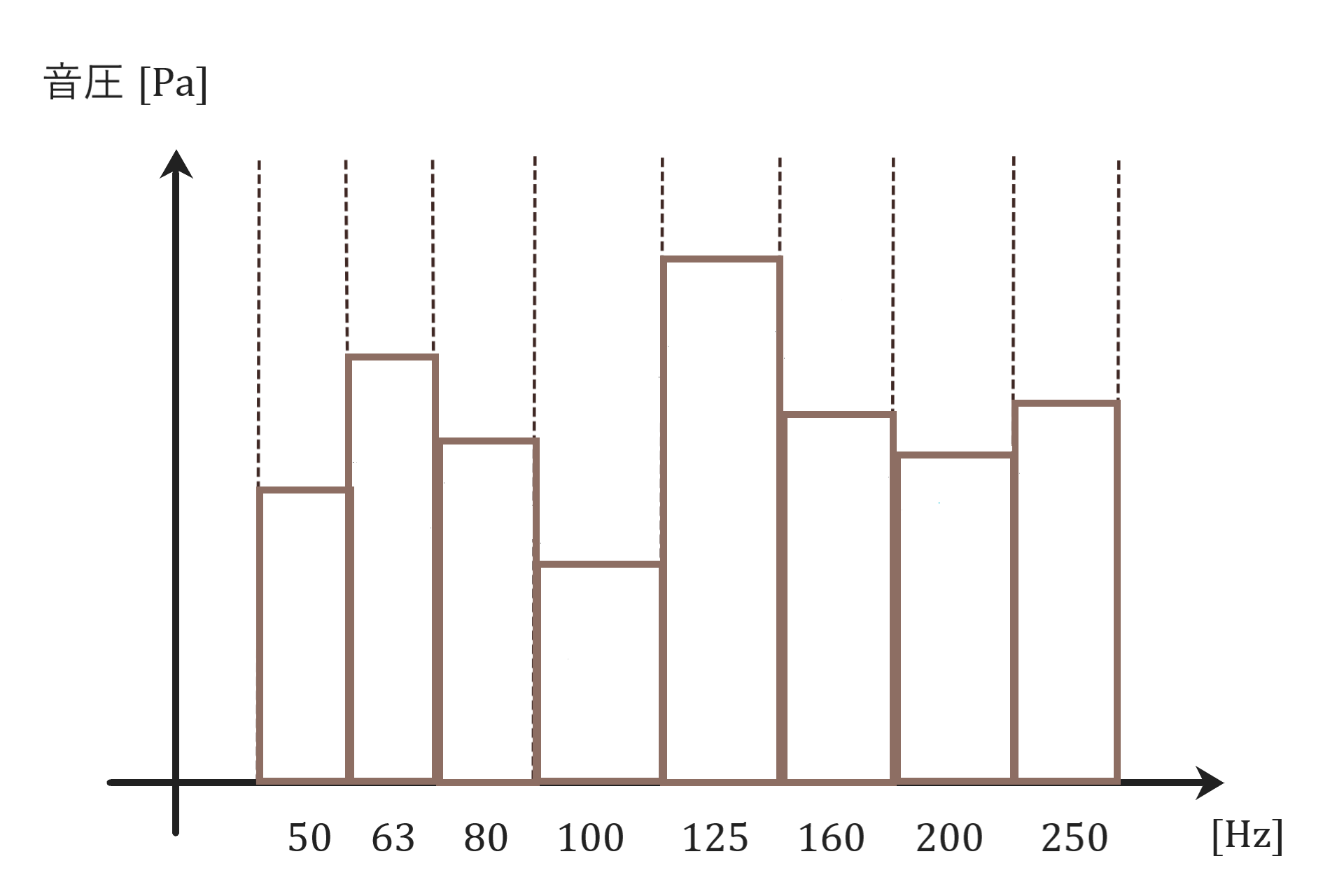
中心周波数をfとして各周波数帯の音圧に
exp[-0.1151α(f)s]を掛けて減衰後のグラフを求めます。
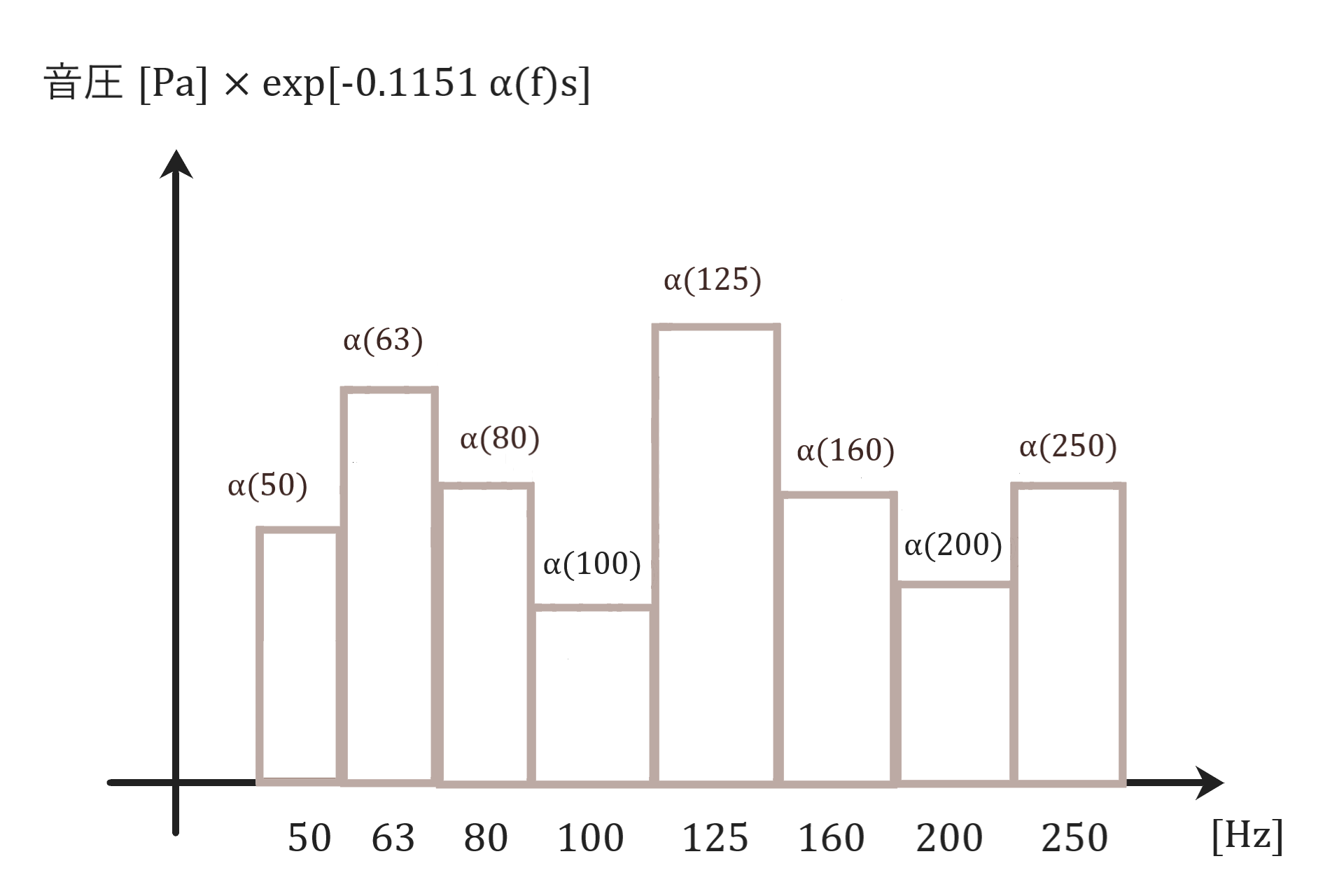
(減衰係数αをfの関数として見ています)
例えば中心周波数50Hzの周波数帯の音圧には
exp[-0.1151α(50)s]を掛けます。
精確な方法
上のやり方は中心の周波数に対応する減衰係数のみで
周波数帯に含まれるすべての音の減衰を
求めてしまう近似的な方法です。
それでも十分実用に耐えます。
より精確に計算したい時は
周波数帯の各音の減衰を個々に求め
足し合わせるスペクトル積分をします。
ただしこの計算にはとても時間がかかること。
また、そこまで細かく計算できたとしても
測定器の誤差があるため限界はあります。
まとめ
空気中を伝搬する音の減衰する理由は主に
エネルギーの分散と空気吸収の2つあり
後者は騒音など広域にわたる
問題で特に重要になって来ます。
空気吸収の計算には減衰係数αが必要で
(1m進むごとにαデシベル減衰します)
式から求めることも可能ですが複雑なため
JISに載っている表を利用すると便利です。
高音の速やかな減衰、
音の減衰の実用的な求め方まで説明できました。
誤差評価など、より詳しくは参考文献を当てってみて下さい。
参考文献
JISを見るにはアカウントを作ります。
上手くログインできない場合
ユーザーIDとパスワードは手入力してみて下さい。
