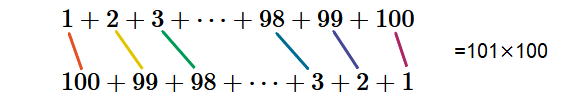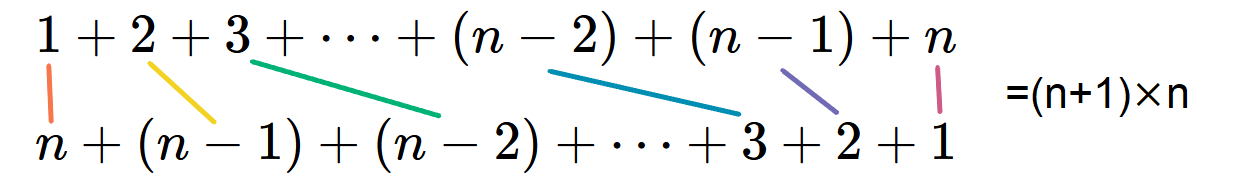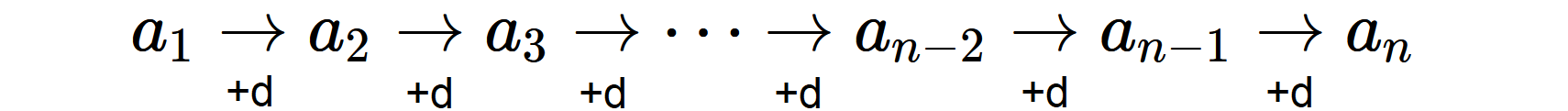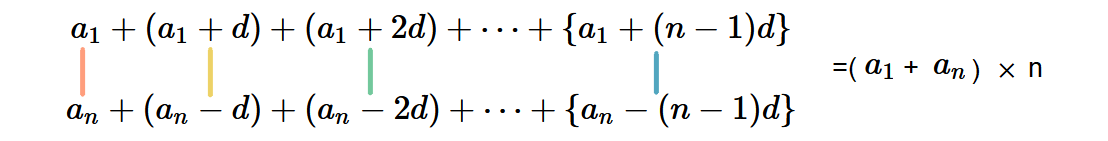１から100まで足すと5050、
等差数列の和の公式を楽しく勉強っ！

１から100まで足すと5050になるのは有名な事実です。

この記事では
１から100までの足し算をパズルみたいに楽しく解いた後、

学校で習う「等差数列の和の公式」
まで合わせて説明したいと思います♪

１から100まで足すと5050

１から100まで足した数を求めるには、次のように考えます。

１から100までの足し算と、
100から１までの足し算を上下に並べます。

すると足したら101になるペアを100個、作れました。

これは式にすると、

$$(1+2+3+\cdots+98+99+100)\times2=101\times100$$

なので、両辺を２で割って

$$1+2+3+\cdots+98+99+100=101\times50$$

101×50=5050より１から100まで足すと5050でした！

１からｎまで足すと？

同じ方法で１からnまでの足し算も計算できます。

１からnまでの足し算と
nから１までの足し算を上下に並べて、

これを式に起こすと

$$\{1+2+3+\cdots+(n-2)+(n-1)+n\}\times2=n(n+1)$$

両辺を２で割ると、

$$1+2+3+\cdots+(n-2)+(n-1)+n=\frac{n}{2}(n+1)$$

です。

等差数列の和の公式

いよいよ等差数列の和の公式にチャレンジします。

等差数列とは一つ進むごとに決まった数d
だけ増えて行く数列のことです。

これを全部足したらいくつになるでしょう？という問題です。

難しそうですがやることは同じです。

初めの数から最後の数までの足し算と
最後の数から初めの数までの足し算を上下に並べます。

$$a_1+a_2+a_3+\cdots+a_n$$

$$a_n+a_{n-1}+a_{n-2}+\cdots+a_1$$

これは

と書き直せます。
（dを足すと一つ先の数、引くと前の数になるので）

式に起こすと

$$(a_1+a_2+a_3+\cdots+a_n)\times2=n(a_1+a_n)$$

より等差数列の公式

$$a_1+a_2+a_3+\cdots+a_n=\frac{n}{2}(a_1+a_n)$$

が求まりました！

ちなみに、１から100までの足し算もこの公式を使えば一発です。

$$a_1=1, \quad a_n=100, \quad n=100$$

を代入すれば良くて、

$$1+2+3+\cdots+100=\frac{100}{2}\times(1+100)=5050$$

確かに合ってます♪

まとめ

順番を入れ換えた数列を二つ、
上下に並べて足すとパズルみたいに簡単になることを見て来ました。
これでもう等差数列の和の公式は怖くありません (*‘ω’*)=3