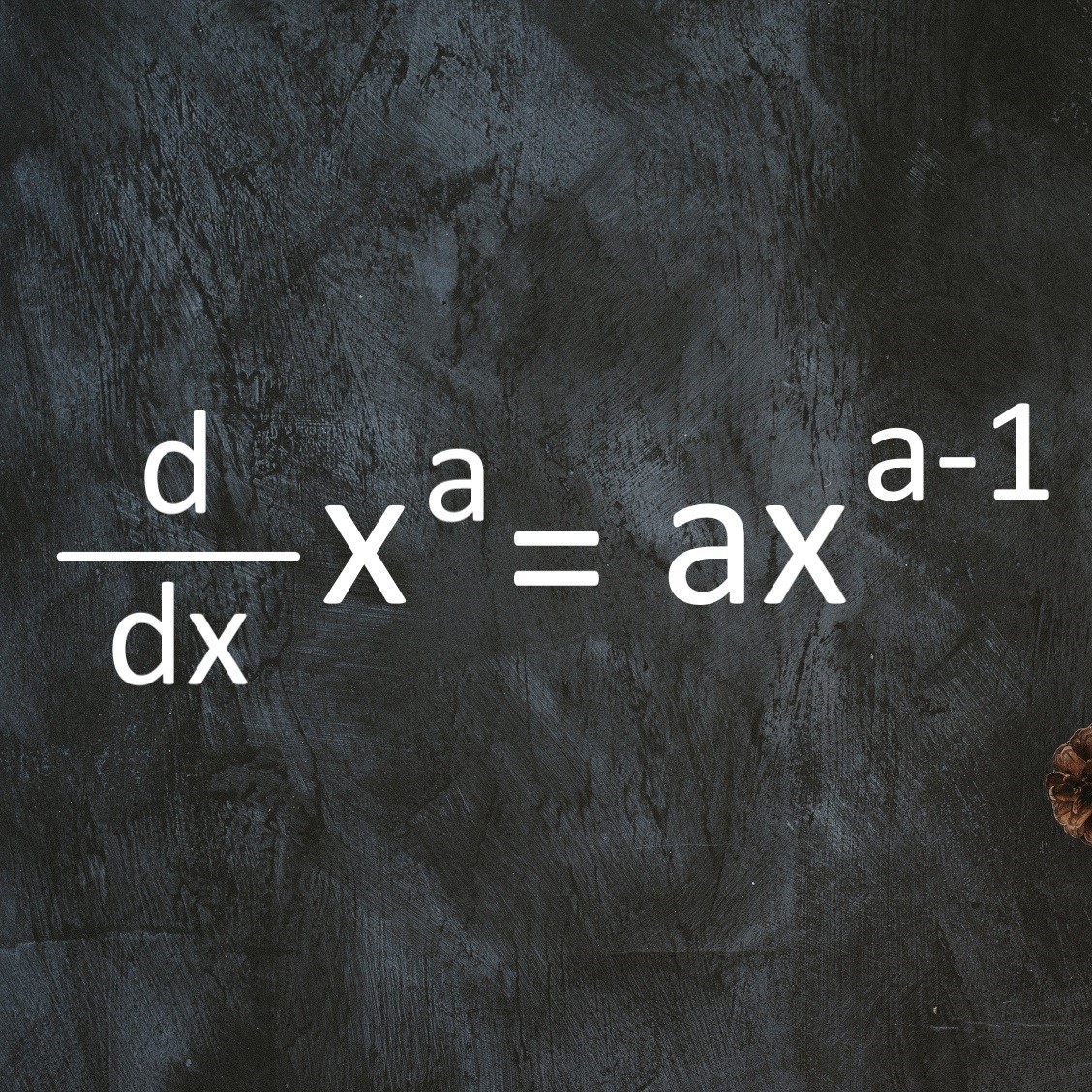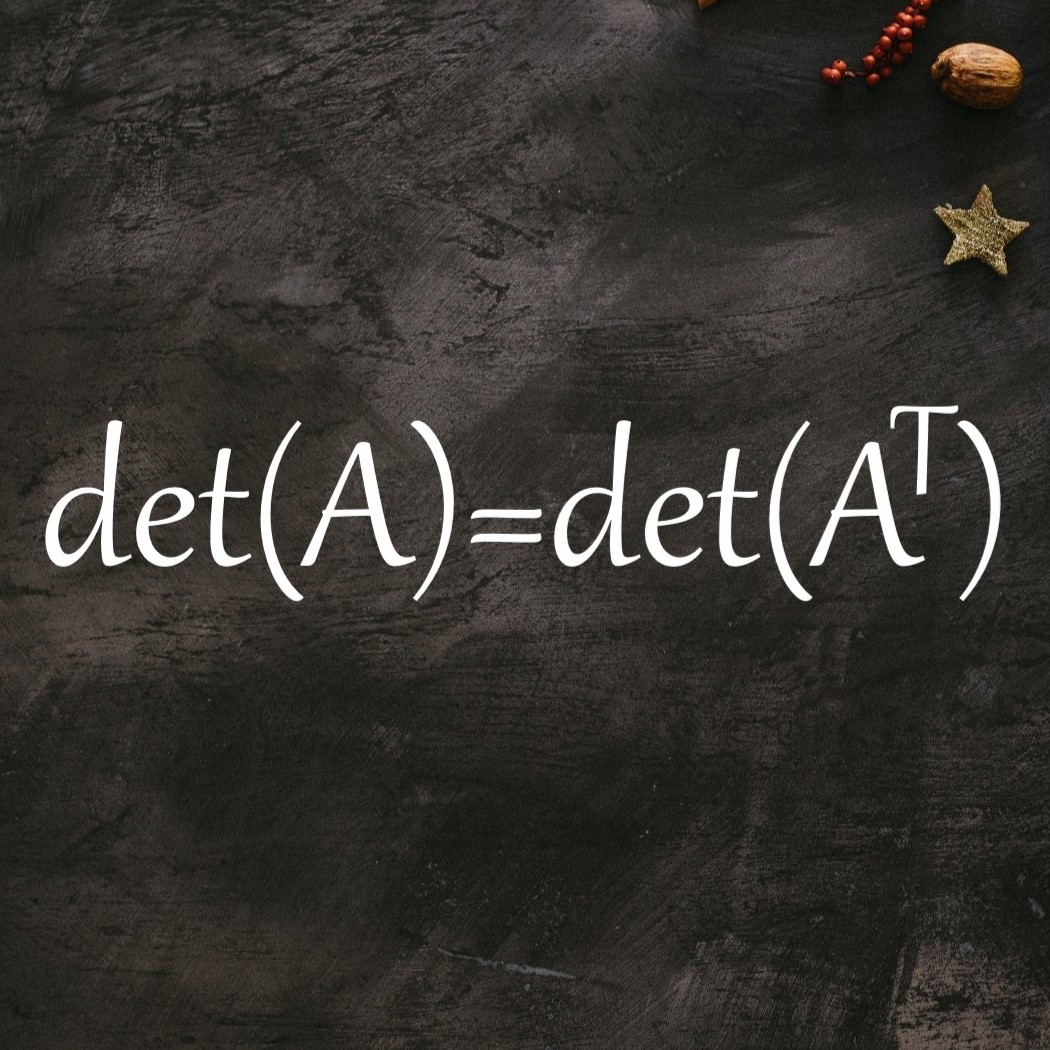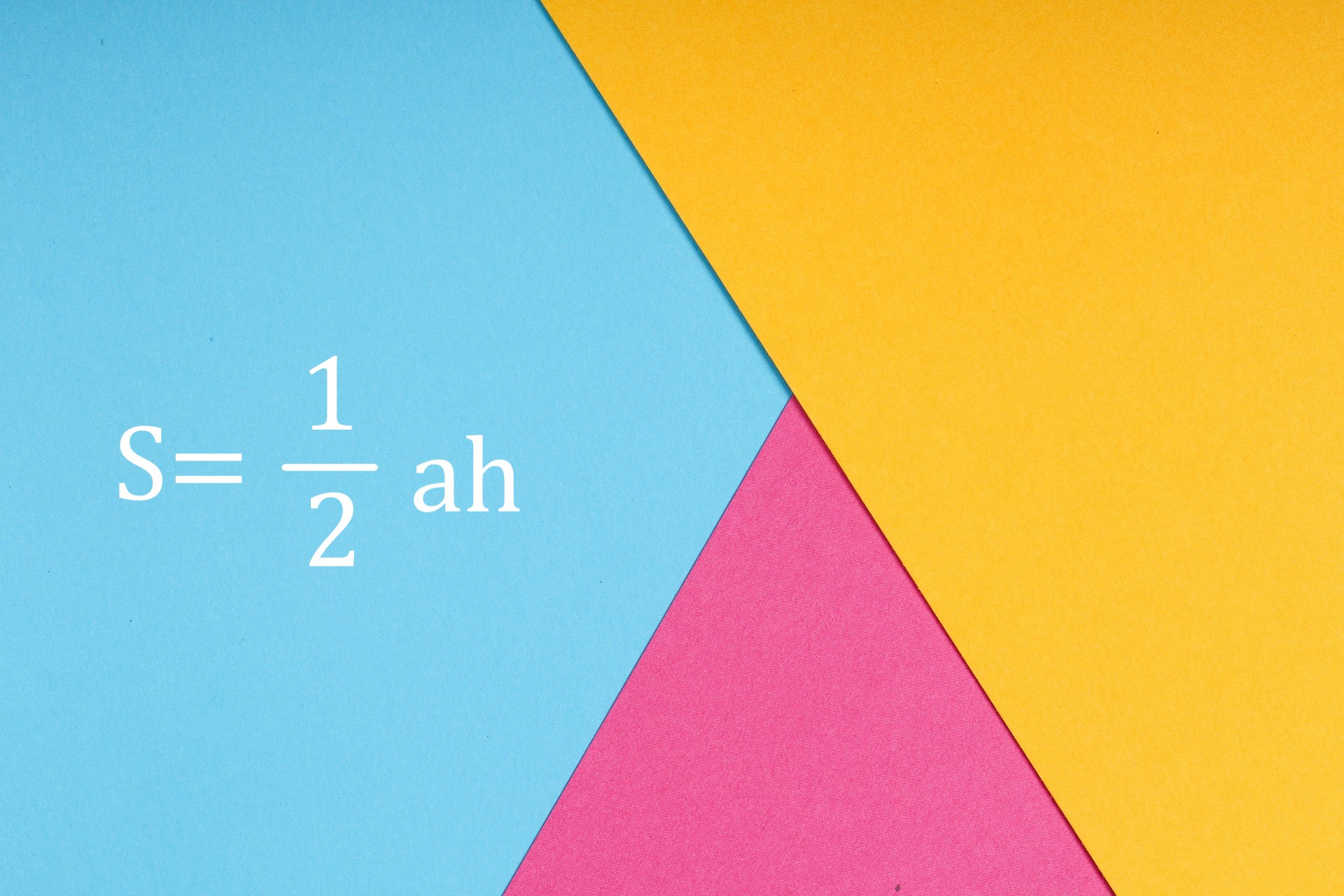shoma

行列Aとその転置行列ATの 行列式は等しい事が知られています。 なるべく行間は少なく、 分かりやすさ重視で証明したいと思います。 n文字の置換と符号は勉強済みとします。 行列式の転置不変性 補題を二つ用意します。 逆置換の符号補題 置換σと、その逆置換σ-1の符号は等しい。 証明 単位置換をεとして \( \sigma^{-1} \sigma = \epsilon \) である。 \( \quad\, \mathrm{sgn} ( \sigma^{-1} \sigma )= \mathrm{sgn} (\ ...

じゃんけんの勝ち負けは運、公平な決め方と言われますが 実際には、 相手の心を読む心理学勝ちやすい手を分析する統計学 に精通している人の方が有利です。 最大の問題である”先出し”について解説して じゃんけんへの疑問を解消します。 じゃんけんの問題点 じゃんけんには、 手を出すタイミングを合わせるのが難しい という問題点があります。 こちらの動画をご覧ください。 これは審判付きのじゃんけんの公式試合で、 ３回の手を出し合う素振りでタイミングを合わせた後 ４回目の本番で勝負する方式が採られています。 タイミング ...

三角形の面積は 底辺×高さ÷２、三角関数、法線ベクトル、ヘロンの公式 など沢山の方法で求まります。 行列式を用いると ３次元空間内の三角形の頂点の座標が分かっている時 最も速く汎用性高く計算する事ができます。 始めに、平面上の三角形から説明して 空間内の三角形へと繋げます。 線形代数の基礎、行列式 定理の証明はかなり難しいです。 ３点が同一平面上にある場合 原点を頂点に持つ三角形 三角形の面積（基本） 原点O(0, 0)、点A(a1, a2)、点B(b1, b2)により作られる三角形の面積は $$ \fr ...

べき関数は高校数学において 一次関数、二次関数や分数関数、無理関数など 色々な名前で登場し 気付いたらべき関数と知らずに勉強が済んでいる、という代物です。 べき関数の定義と諸性質を グラフを描きつつ、わかりやすく説明したいと思います。 べき関数の定義 aを実数として \( y = x^a \) の様に書かれる関数をべき関数と呼びます。 漢字だと巾関数、または冪関数です。 aを自然数nに限れば \( y = x^n \) お馴染みの一次関数や二次関数になります。 例えばy=xは最も良く知られたべき関数です。 ...

オンラインくじでアニメグッズを手に入れると （期待値では）普通に買うより安く済みます。 この記事では、これからオンラインくじを買ってみたい人向けに 良いくじを見分ける５つのポイントをまとめて、 推しお迎えの支援をしたいと思います。 この記事はDMM、アニメイト、ゲーマーズのPRを含みます。 好みの作品の有無 最初にチェックすべきは です。 アニメの人気作、ラノベ、少女漫画、ジャンプ系、VTuber など力を入れてる分野がオンラインくじによって変わるので、 趣味嗜好の合う物を探します。 https://sh ...

積分の値はリーマンの定義通りには求めづらく 一変数の場合、積分と微分が逆の操作である事を利用して解きました。 重積分についても同様に難しく、 この場合は一変数の積分に分ける逐次積分と呼ばれる方法をとります。 逐次積分は直感的には成立して当然かつ 条件も関数の連続性のみなので定理として忘れられがちです…。 この記事では逐次積分を学び直し 積分領域の範囲の定め方や順序交換、 ガウス積分、フビニの定理との関連性まで書いて行きます。 逐次積分の定理 長方形 逐次積分の定理（長方形） f(x, y)がΩ=[a, b ...

x2、sinx、等を見ていると 関数が実数全体を定義域に持つ事は当然に感じられると思います。 指数関数axは特殊で、始めはxが自然数の時のみ値を持ちます。 この記事では xが自然数でない時について累乗の定義のされ方と理由、 指数関数の逆として対数関数が生まれ 最終的に指数が複素数まで拡張し得る所まで。 指数関数の導出過程をまとめます。 指数関数の出発点 指数関数は累乗（べき乗）から始まります。 累乗とは何かと言うと、 同じ数aを自然数n回掛け合わせる計算の事です。 $$\underbrace{ a \ti ...

この記事では大学数学の無理数乗の定義を説明します。 合わせて、無理数乗により指数関数が作られ 単調増加かつ連続な事を証明してくれているサイト様を紹介し、 最後に高校数学の無理数乗の定義に落ち着く所まで書きたいと思います。 実数の連続性公理、指数法則、ε-δ論法 無理数乗の定義 a>1の場合 実数a>1について無理数x乗を 無理数乗の定義（a>1） \( a^x := \sup \{ a^r \, | \, r \in \mathbb{Q}, \quad r <x \} \) で定義 ...

近年ASMRが人気になってそれを意識したゲームも増えたかなと思います。 この記事では、 ASMRを楽しめる無料ゲームを見つけ次第紹介します。 現在のゲーム数は１つです…。 Bubble Fall 同じ色の球を３つ揃えると落ちて来るお馴染みのゲーム。 球の配置が規則的かつカラフルで視覚的ASMR効果を得られます。 グラフィックや音も綺麗に作り込まれ、遊んでいると眠たくなります。 Bubble Fallで遊ぶ

有理数乗について指数法則が成り立ちます。 この記事では 有理数乗の定義から始めて、有理数乗の指数法則を証明します。 有理数乗の指数法則 実数a、b>0と有理数r、sは次の３つの等式を満たします。 有理数乗の指数法則 \( a^r a^s = a^{r+s} \) \( (a^r)^s = a^{rs} \) \( (ab)^r = a^r b^r \) 定義の確認 1/n乗 自然数nについて 1/n乗の定義 \( a^{1/n} := x \) \( ( x^n = a, \quad x > ...